ガウスの発散定理再考

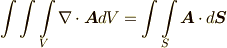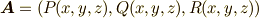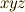この記事では，ベクトル解析に出てきたガウスの発散定理を微分形式の枠組みで考え直します．ガウスの発散定理は，ベクトル形では $\int \int \int \limits _{V} \nabla \cdot \bm{A} dV = \int \int \limits _{S} \bm{A} \cdot d\bm{S}$ と書けますが，ここでは $\bm{A}=(P(x,y,z),Q(x,y,z),R(x,y,z))$ として， xyz 座標系で成分表示した形から議論を始めます．

theorem

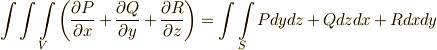
$\int \int \int \limits _{V} \left( \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z} \right) = \int \int \limits _{S} Pdydz + Qdzdx + R dxdy$

微分形式にしてみる

まず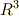， $R^{3}$ 上の二次微分形式 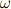$\omega$ を考えます．

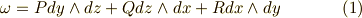
$\omega = P dy \land dz + Q dz \land dx + R dx \land dy \tag{1}$

また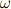， $\omega$ の外微分を求めておきます．もう，外微分の途中計算は省略します．

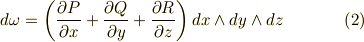
$d\omega = \left( \frac{\partial P}{\partial x } + \frac{\partial Q}{\partial y } + \frac{\partial R}{\partial z } \right) dx \land dy \land dz \tag{2}$

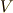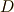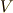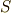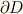領域をと書き直し，の境界（表面）であるを $\partial D$ と命名することにします．これは，名前の付け替えに過ぎません．さて，式 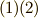(1)(2) と，この新しい名前に従うと，ガウスの発散定理の両辺は次のように書き換えることができます．

$\int \limits _{\partial D} d\omega = \int \limits _{D} \omega \tag{3}$

微分形式で表現すると，かなりすっきりと表現できました．ところで，私達は平面のグリーンの定理再考で，平面のグリーンの定理も微分形式を使って書き直してみました．その表現は，次のようになるのでした．

$\int \limits _{\partial D} \omega = \int \limits _{D} d\omega \tag{4}$

なーんと，これは式 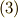(3) とまったく同じ形をしています！！つまり，これらは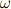（ $\omega$ の階数に違いはありますが）どうやら同じ定理だったと考えることが出来そうです．

[*]	ベクトル解析を勉強したとき個別に覚えていた定理に，微分形式によって統一的視点が与えられました．数学は，レベルが上がってくると，覚えることが減っていくようです．カリスマ収納上手主婦も，数学を勉強すれば，きっともっと収納上手になれることでしょう．なんのこっちゃ．

もちろん，まだ形が同じだからと言って，同じ定理なのだと断定することは出来ませんが，そのことは多様体を勉強したあとできちんと証明する予定です．平面のグリーンの定理，ガウスの発散定理と来れば，次はストークスの定理ですね．この調子で，とりあえずストークスの定理も微分形式で書き直してみましょうo(^ ^)o．

[home] [微分形式] [ページの先頭]