ストークスの定理再考
ここまでに,ベクトル解析で重要だった 平面のグリーンの定理 と ガウスの発散定理 が,どちらも微分形式を使えば次のように書けてしまうことを見ました.

式 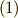 はとても簡単な形ですし,背後にある何かしらの『美』を感じさせる式です.さて,ベクトル解析で重要な積分定理には,もう一つ ストークスの定理 がありました.
はとても簡単な形ですし,背後にある何かしらの『美』を感じさせる式です.さて,ベクトル解析で重要な積分定理には,もう一つ ストークスの定理 がありました.
theorem
【ストークスの定理】閉曲線 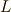 を境界とする曲面
を境界とする曲面  上で,
上で,  級ベクトル値関数
級ベクトル値関数 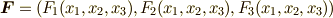 が定義されています.ただし領域
が定義されています.ただし領域  は単連結とします.このとき
は単連結とします.このとき 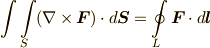 が成り立ちます.
が成り立ちます.
この記事では,まず,ストークスの定理を微分形式を使って定式化し直すことを考えます.もっとも,既に,平面のグリーンの定理とガウスの発散定理を微分形式で表現していますので,説明で共通する部分は少し省略します.
ストークスの定理再考
ストークスの定理で, 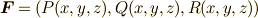 ,
, 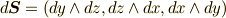 ,
, 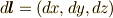 と置き,
と置き,  を
を 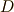 ,
, 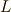 を
を 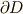 と置くと,ストークスの定理は次式のように表現されることになります.
と置くと,ストークスの定理は次式のように表現されることになります.
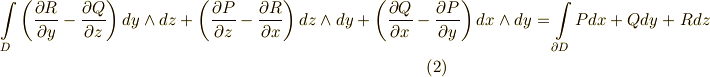
これに対し,一次微分形式を 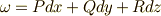 と定義すると,式
と定義すると,式  の右辺は
の右辺は  と書けます.左辺を考えるために,
と書けます.左辺を考えるために,  の外微分
の外微分  を考えます.
を考えます.
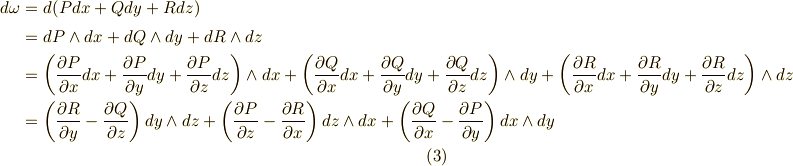
式  と式
と式  から,ストークスの定理も次式のように定式化することが出来ることが分かります.
から,ストークスの定理も次式のように定式化することが出来ることが分かります.

結局,平面のグリーンの定理,ガウスの発散定理,そしてストークスの定理の三つともが,全て同一の形で書けることが分かりました.(これからは,式 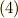 を一つだけ覚えておけばいいですね♪)
を一つだけ覚えておけばいいですね♪)
これから示すこと
平面のグリーンの定理,ガウスの発散定理,ストークスの定理の三定理をどれも式 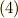 の形に帰着させてみましたが,議論のスタートポイントは,それぞれ個別に行った古典的な証明を基にしていました.つまり,私達は,定理を個別に式
の形に帰着させてみましたが,議論のスタートポイントは,それぞれ個別に行った古典的な証明を基にしていました.つまり,私達は,定理を個別に式 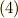 の形に変形させられることを『見てみた』だけで,『一般に,全ての次数の微分形式
の形に変形させられることを『見てみた』だけで,『一般に,全ての次数の微分形式 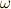 に対して式
に対して式 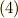 は言えるのか?』という,十分条件を証明したわけではありません.
は言えるのか?』という,十分条件を証明したわけではありません.
でも,読者の多くの方は,既に,『式 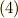 は普遍的な定理なんじゃないか?』と薄々予想していることと思いますo(^ ^)o.この後,このことを確認する作業に入りますが,まず 微分形式の引き戻し という概念を勉強し,それから, 面積素と微分形式 で考えたような,積分の向きと微分形式の関係をもう少し整理します.(積分の向きと微分形式の関係がまだ曖昧ですし,私達は微分形式の積分というものをちゃんと定義していません.私達は,いま微分形式を主に三次元ユークリッド空間の枠組みで考えています.まず,この枠組みの中で, ストークスの定理再々考 の記事で,ストークスの定理とグリーンの定理が同じ定理であることを微分形式を使って示します.一般の次数に定理を拡大するためには,多様体という概念を勉強する必要があり,証明はもう少し後になります.
は普遍的な定理なんじゃないか?』と薄々予想していることと思いますo(^ ^)o.この後,このことを確認する作業に入りますが,まず 微分形式の引き戻し という概念を勉強し,それから, 面積素と微分形式 で考えたような,積分の向きと微分形式の関係をもう少し整理します.(積分の向きと微分形式の関係がまだ曖昧ですし,私達は微分形式の積分というものをちゃんと定義していません.私達は,いま微分形式を主に三次元ユークリッド空間の枠組みで考えています.まず,この枠組みの中で, ストークスの定理再々考 の記事で,ストークスの定理とグリーンの定理が同じ定理であることを微分形式を使って示します.一般の次数に定理を拡大するためには,多様体という概念を勉強する必要があり,証明はもう少し後になります.
ストークス
ストークスの定理や,流体力学のナヴィア・ストークス方程式にその名をとどめるストークス(  )は,アイルランド北西部の海辺の町, スクリーン に生まれました.ストークスの父は牧師で,母も牧師の娘であり,ストークスの三人の兄弟も全員牧師になっています.非常に宗教的な家庭環境に生まれたようです.しかし,ストークスの父も非常に高い教育を受けた人で,父親や信者の人から,学校に行く前からラテン語をはじめとする教育を受けたようです.その後,ストークスはイングランドのブリストルで教育を受けますが,数学の才能を認められ,ケンブリッジ大学へ進みます.
)は,アイルランド北西部の海辺の町, スクリーン に生まれました.ストークスの父は牧師で,母も牧師の娘であり,ストークスの三人の兄弟も全員牧師になっています.非常に宗教的な家庭環境に生まれたようです.しかし,ストークスの父も非常に高い教育を受けた人で,父親や信者の人から,学校に行く前からラテン語をはじめとする教育を受けたようです.その後,ストークスはイングランドのブリストルで教育を受けますが,数学の才能を認められ,ケンブリッジ大学へ進みます.
終生,敬虔なキリスト教徒だったストークス.質素で慎ましい生活を送った.
ケンブリッジ大学ではホプキンス  の数学観に強い影響を受け,物理数学の方面に興味が向きます.ストークスの研究は,流体力学,光学に多く,特にナヴィア・ストークス方程式は,粘性流体の基礎方程式として,流体力学で最も重要な方程式となっています.
の数学観に強い影響を受け,物理数学の方面に興味が向きます.ストークスの研究は,流体力学,光学に多く,特にナヴィア・ストークス方程式は,粘性流体の基礎方程式として,流体力学で最も重要な方程式となっています.
| [*] | ナヴィア・ストークス方程式は,ストークスより前にナヴィア(  ),ポアソン ),ポアソン  等によって研究されていました.ナヴィア・ストークス方程式に解析的な厳密解があるかどうかは,未だに数学的には証明されておらず,大きな未解決問題になっています.(もっとも,流体力学者は,数値計算によって解をじゃかじゃか求めています.) 等によって研究されていました.ナヴィア・ストークス方程式に解析的な厳密解があるかどうかは,未だに数学的には証明されておらず,大きな未解決問題になっています.(もっとも,流体力学者は,数値計算によって解をじゃかじゃか求めています.) |
奇妙なことに,ストークスは 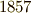 年の結婚に前後して,数学や理論物理への興味を失い,実験に没頭するようになります.実験内容は物理にとどまらず,化学や植物学にまで及んだようですが,こちらの方面ではあまり大きな貢献は無いようです.ずっと数学だけやっていてくれたら,と惜しまれます.
年の結婚に前後して,数学や理論物理への興味を失い,実験に没頭するようになります.実験内容は物理にとどまらず,化学や植物学にまで及んだようですが,こちらの方面ではあまり大きな貢献は無いようです.ずっと数学だけやっていてくれたら,と惜しまれます.