平面のグリーンの定理再考

ベクトル解析に，平面のグリーンの定理と呼ばれる定理がありました．

theorem

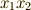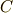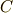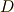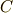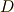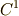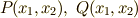【平面のグリーンの定理】 $x_{1}x_{2}$ 平面上に単純閉曲線と，に囲まれた領域があり，とを含む領域で定義された $C^{1}$ 級の関数 $P(x_{1},x_{2}), \ Q(x_{1},x_{2})$ があります．このとき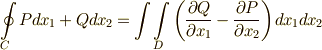， $\ointop \limits _{C}Pdx_{1}+Qdx_{2} = \int \int \limits _{D} \left( \frac{\partial Q}{\partial x_{1}}- \frac{\partial P}{\partial x_{2}} \right) dx_{1}dx_{2}$ が成り立ちます．ただし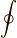， $\ointop$ の向きは反時計回りとします．

証明や詳細については平面のグリーンの定理を参照して下さい．この記事では，この定理を微分形式を使って定式化し直すことを考えます．

微分形式による表現

まず，この問題は二次元ベクトル空間 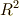$R^{2}$ 上で考えますから，微分形式として出て来るのは零次微分形式（ただの関数），一次微分関数，二次微分関数までです．（三次微分形式以降は零になります．よく分からない人は，もう一度微分形式と外微分を復習して下さい．）定理の左辺の線積分の中身は，一次微分形式の形をしていますね．それを 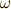$\omega$ で書くことにします．

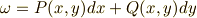
$\omega = P(x,y)dx+Q(x,y)dy$

さて，次に 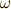$\omega$ の外微分を取ってみましょう．

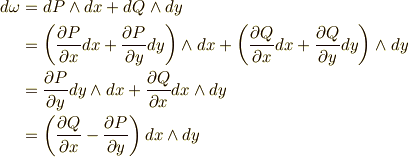
$d\omega &= dP \land dx + dQ \land dy \\&= \left( \frac{\partial P}{\partial x}dx + \frac{\partial P}{\partial y}dy \right) \land dx + \left( \frac{\partial Q}{\partial x}dx + \frac{\partial Q}{\partial y}dy \right) \land dy \\ &= \frac{\partial P}{\partial y}dy \land dx + \frac{\partial Q}{\partial x}dx \land dy \\& = \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) dx \land dy$

まだウェッジ積の計算に馴れていない人がいると思いますが，途中で 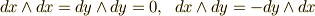$dx \land dx = dy \land dy =0, \ \ dx \land dy = -dy \land dx$ を使ったことを確認して下さい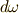． $d\omega$ を前出の平面のグリーンの定理と比較してみると，まさに右辺の形になっていることが分かると思います．また，『周回積分の向きは，反時計回りとする』という注意をわざわざ別に書き添えなくても，積分の向きと微分形式の議論により，そうした向きの情報も微分形式に含めることが出来ます．安心ですねー．よって，グリーンの定理は，微分形式を使って次のように表現できます．

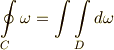
$\ointop \limits _{C} \omega = \int \int \limits _{D} d\omega$

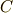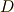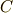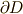これだけでも十分に簡単で，最初よりもずっと覚えやすい形をしていますが，曲線は曲面の境界ですから，を形式的に $\partial D$ と表現すると，もっと綺麗な形に帰着します．せっかくなので，もう一度定理の形に書き下しておきます．

theorem

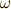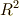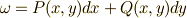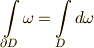【平面のグリーンの定理】 $\omega$ を $R^{2}$ 上の一次微分形式 $\omega = P(x,y)dx+Q(x,y)dy$ とすると， $\int \limits _{\partial D} \omega = \int \limits _{D} d\omega$ が成り立ちます．

いやー，本当に美しいですね．最初に掲げた定理の表現より，ずっとすっきりしています．しかも，この表現で何が美しいかと言えば，見て分かる通り，被積分関数と積分領域との間に，一種の 双対関係 とも言うべき関係が見えることです．

[*]

平面のグリーンの定理に関して何よりも重要な性質は，この定理が『座標系の取り方によらない』という事実です．言い換えれば，（微分形式で表現した）平面のグリーンの定理は座標変換しても不変です．そして外微分の座標不変性で示したように，外微分による表現は座標系によりませんので，微分形式によって 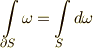$\int \limits _{\partial S} \omega = \int \limits _{S} d\omega$ と書いた表現は座標系によらないわけです．実は，ベクトル解析に出てきたガウスの発散定理，ストークスの定理なども，平面のグリーンの定理と同じであることが徐々に分かってきます．そして，平面のグリーンの定理，ガウスの発散定理，ストークスの定理などは，どれももっと包括的な定理の系であることが示されます．

[home] [微分形式] [ページの先頭]