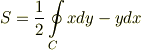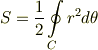平面のグリーンの定理
一つ前の記事では,体積分と面積分を関係づける ガウスの発散定理 を勉強しました.この記事では,面積分と線積分を関係付ける グリーンの定理 と呼ばれる定理を勉強します.
| [*] | 考えるのは,平面上の閉曲線と,その閉曲線の囲む領域に関する面積分ですので,表題は特に『平面のグリーンの定理』としました.平面のグリーンの定理は,実は,もっと一般的に空間内の閉曲面に関してなりたつ ストークスの定理 の特別な場合に過ぎないのですが,(平面の)グリーンの定理と,別名で呼ばれることが多いです.グリーンの定理と呼ばれる別の定理も後で紹介する都合上,この定理の名前には『平面の』を冠することとします. |
theorem
【平面のグリーンの定理】 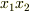 平面上に単純閉曲線
平面上に単純閉曲線 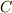 と,
と, 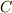 に囲まれた領域
に囲まれた領域 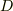 があり,
があり, 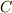 と
と 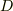 を含む領域で定義された
を含む領域で定義された 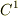 級の関数
級の関数 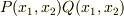 があります.このとき,
があります.このとき, 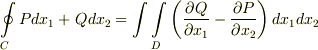 が成り立ちます.
が成り立ちます.
単純閉曲線というのは,自分自身と交わったりしない閉曲線のことです.また, 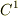 級というのは,少なくとも一階導関数が連続関数だという意味です.
級というのは,少なくとも一階導関数が連続関数だという意味です.
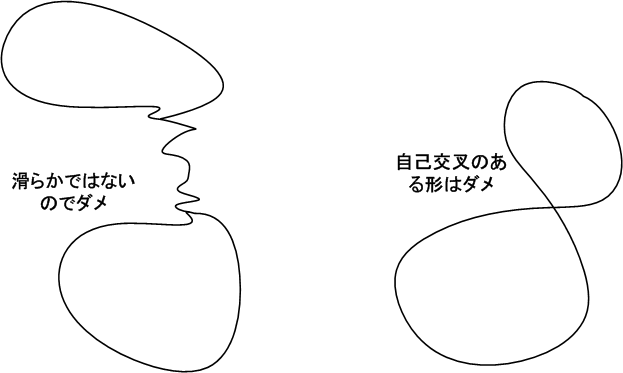
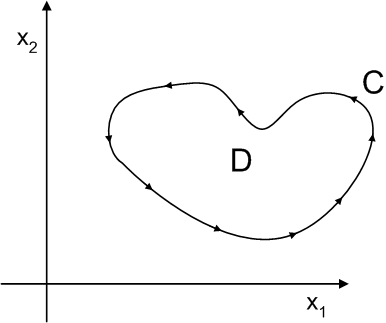
また,線積分の向きは, 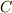 上を
上を 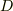 を左手に見ながら回る方向(上図で反時計回り)だとします.定理をじっくり眺めてみて下さい.関数を線積分したものが,関数の一階導関数を面積分したものに等しいというのですね.これは,どういう意味なのでしょうか?とりあえず証明を考えてみましょう.
を左手に見ながら回る方向(上図で反時計回り)だとします.定理をじっくり眺めてみて下さい.関数を線積分したものが,関数の一階導関数を面積分したものに等しいというのですね.これは,どういう意味なのでしょうか?とりあえず証明を考えてみましょう.
proof
まず, 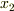 軸に平行で
軸に平行で 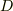 を通る直線は,三つ以上の交点は持たないものとします.(ただし,この仮定は積分領域を分割することで外すことが可能です.後述します.)領域
を通る直線は,三つ以上の交点は持たないものとします.(ただし,この仮定は積分領域を分割することで外すことが可能です.後述します.)領域 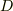 を
を 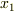 軸上に射影した区間を
軸上に射影した区間を ![[a,b]](./2c3d331bc98b44e71cb2aae9edadca7e.png) ,
, 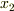 軸上に射影した区間を
軸上に射影した区間を ![[\alpha , \beta]](./741005130342585e2066d9d4496f4d51.png) とすると,
とすると, 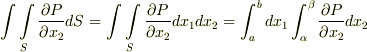 が成り立ちます.(図1を参照してください.)ここで,
が成り立ちます.(図1を参照してください.)ここで, 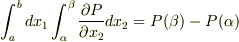 ですので,図の曲線
ですので,図の曲線 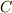 の下側を
の下側を 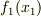 ,上側を
,上側を 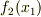 として
として ![\int \int \limits _{S} \frac{\partial P}{\partial x_{2}}dS = \int_{a}^{b} [ P(x_{1}, f_{2}(x_{1}))- P(x_{1}, f_{1}(x_{1}))] dx_{1}](./c6c01894a2d23ab9096d24a53c45f86e.png) が成り立ちます.この右辺は,変数
が成り立ちます.この右辺は,変数 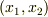 が
が 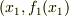 と
と 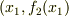 に制限されていますので,結局
に制限されていますので,結局 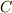 に沿った線積分になっています.線積分の向きは反時計回りに回る向きだったことに注意すると,
に沿った線積分になっています.線積分の向きは反時計回りに回る向きだったことに注意すると, ![\int_{a}^{b} [ P(x_{1}, f_{2}(x_{1}))- P(x_{1}, f_{1}(x_{1}))] dx_{1} = - \ointop \limits _{C} Pdx_{1}](./d38e10610dbb5ad3a2247bbcdd5218f0.png) が言えます.同様に
が言えます.同様に 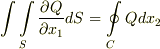 も別個に言えます.周回積分の符号にだけ気をつけて下さい.二式を足して定理が示されます.■
も別個に言えます.周回積分の符号にだけ気をつけて下さい.二式を足して定理が示されます.■
証明の中で, 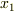 軸や
軸や 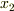 軸に平行な直線は,領域
軸に平行な直線は,領域 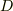 と三点以上で交わることはないと仮定しました.これは,曲線
と三点以上で交わることはないと仮定しました.これは,曲線 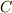 が至るところ外側に凸だと仮定することと同じです.しかし,次図のように,穴がある領域や凹凸のある領域でも,穴のない,外側に凸な小領域に分割すれば,境界線では線積分の向きが逆となって互いに打ち消しあうため,結局,こうした領域でも平面のグリーンの定理が成り立つことを示せます.(全く同じ議論を ガウスの発散定理 でしています.ご参照ください.)
が至るところ外側に凸だと仮定することと同じです.しかし,次図のように,穴がある領域や凹凸のある領域でも,穴のない,外側に凸な小領域に分割すれば,境界線では線積分の向きが逆となって互いに打ち消しあうため,結局,こうした領域でも平面のグリーンの定理が成り立つことを示せます.(全く同じ議論を ガウスの発散定理 でしています.ご参照ください.)
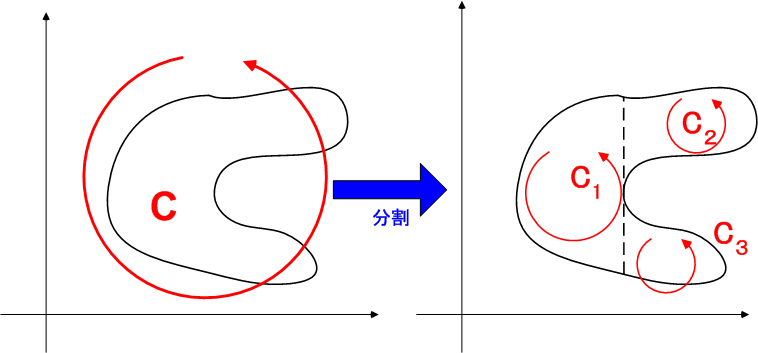
結論として, 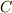 が 区分的に滑らか であれば(つまり,尖がった点がせいぜい有限個くらいしか無い形ならば),平面のグリーンの定理を適用することが可能です.これはかなり緩やかな条件ですから,実質的には,物理の問題に出て来るほとんどの閉曲線と,その囲む領域に対し,平面のグリーンの定理が使えます.
が 区分的に滑らか であれば(つまり,尖がった点がせいぜい有限個くらいしか無い形ならば),平面のグリーンの定理を適用することが可能です.これはかなり緩やかな条件ですから,実質的には,物理の問題に出て来るほとんどの閉曲線と,その囲む領域に対し,平面のグリーンの定理が使えます.
| [†] | 証明の中で, 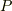 に関する関係式と に関する関係式と 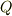 に関する関係式を別々に求め,最後に足し合わせて定理を示しました.しかし,別々に定理を満たす二つの関数を,何もわざわざ足し合わせなくたって良いと思うかも知れません.実は, に関する関係式を別々に求め,最後に足し合わせて定理を示しました.しかし,別々に定理を満たす二つの関数を,何もわざわざ足し合わせなくたって良いと思うかも知れません.実は, 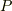 や や 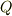 の個別の関係式は座標系の取り方によるのですが,定理として掲げたように, の個別の関係式は座標系の取り方によるのですが,定理として掲げたように, 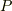 と と 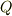 を足し合わせた形にしたものは座標系の取り方と独立になりたつのです.この記事では強調できませんでしたが,平面のグリーンの定理の真価は,座標系と無関係という性質にあります. を足し合わせた形にしたものは座標系の取り方と独立になりたつのです.この記事では強調できませんでしたが,平面のグリーンの定理の真価は,座標系と無関係という性質にあります. |
平面のグリーンの定理を使う上で,周回積分の向きが非常に重要です.最初の図のように,通常は 反時計回りに回る方向を正とします .線積分に向きがあり,面積分には曲面の表裏の区別があったように,周回積分にも向きがあり,これを逆にしたりすると積分の符号が変わってきてしまうのです.ベクトルの積分定理は,必ず向きと一緒に覚えるようにして下さい.
| [‡] | 平面のグリーンの定理は,次に勉強するストークスの定理の特別な場合と考えることができます.さらに広い視野に立った扱いについては 積分定理のまとめと展望 を参照して下さい.座標系によらないという性質は, 微分形式 で勉強します.平面のグリーンの定理は,符号などを含めて少し覚えにくい形をしていますが,微分形式を勉強するともっと簡単に覚えられるようになります. |
演習問題2
次の値を計算してみて下さい. 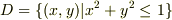 とします.
とします.
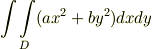
グリーン
グリーンの定理にその名をとどめるグリーン  は,英国ノッティンガムの裕福なパン屋に生まれました.家業は順調で,一家は経済的には不自由なく暮らしましたが,
は,英国ノッティンガムの裕福なパン屋に生まれました.家業は順調で,一家は経済的には不自由なく暮らしましたが, 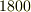 年には内乱のため食料の欠乏した民衆に家を襲撃されるという,イギリス版米騒動のような被害にも遭っています.グリーンの父が建設した粉挽き用の風車は現在もノッティンガムにあるそうですから,お近くを観光の際は足を伸ばしてみて下さい.(ただし,
年には内乱のため食料の欠乏した民衆に家を襲撃されるという,イギリス版米騒動のような被害にも遭っています.グリーンの父が建設した粉挽き用の風車は現在もノッティンガムにあるそうですから,お近くを観光の際は足を伸ばしてみて下さい.(ただし, 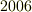 年夏の新聞調査では,ノッティンガムは英国で一番治安の悪い町にランクインしています.)
年夏の新聞調査では,ノッティンガムは英国で一番治安の悪い町にランクインしています.)

現存するグリーン家の風車
グリーンは家業を継ぐために学校も早くに退学したため,少年時代には数学教育を受けておらず,この風車小屋の最上階の部屋で家業を手伝いつつ独習したと考えられています.当時の最先端の学術的情報を,このような遠隔地でどうやって入手し,どのように独学していたのかは謎に包まれていますが,グリーン関数のアイデアや,グリーンの定理の名前で呼ばれる積分定理の,少なくとも幾つかはこの風車の中で完成されたようです.グリーンが発表した論文は,当初あまり人の注目を集めませんでしたが,その後認められ,ケンブリッジ大学に研究のため招かれましたが,健康状態がすぐれず,失意の中,ノッティンガムに帰って亡くなりました.ベクトル解析,ポテンシャル論,微分方程式の境界値問題などの分野おけるグリーンの功績は,グリーンの死後しばらくしてから高く評価されるようになりました.

数学者のグリーンの絵や写真をお持ちの方はぜひ御提供ください.
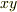 上で,単純閉曲線
上で,単純閉曲線 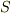 とします.
とします.