積分定理のまとめと展望
ここまでに,ベクトルの積分定理として, ガウスの発散定理 , 平面のグリーンの定理 , ストークスの定理 という三つの定理を勉強しました.変数や積分領域の細かい説明などはここでは省略し,定理の概形だけ再び考えます.
【ガウスの発散定理】

【平面のグリーンの定理】
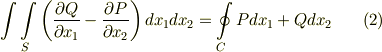
【ストークスの定理】
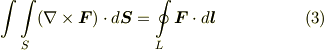
平面のグリーンの定理は,ストークスの定理で 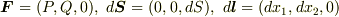 と置けば導けますので,ストークスの定理の特別な場合だと言えます.実質的に勉強したのは,ガウスの発散定理とストークスの定理の二つだけです.それから,特に個別の名前はありませんが,ガウスの発散定理をスカラー関数
と置けば導けますので,ストークスの定理の特別な場合だと言えます.実質的に勉強したのは,ガウスの発散定理とストークスの定理の二つだけです.それから,特に個別の名前はありませんが,ガウスの発散定理をスカラー関数 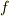 に応用すると次の関係式も得ます.(式
に応用すると次の関係式も得ます.(式 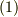 の成分を一つ考えれば良いだけです.)
の成分を一つ考えれば良いだけです.)
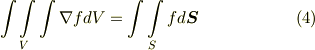
さらに『スカラーポテンシャルを持つベクトルの線積分は積分経路によらない』という式も書いておきます.
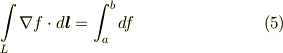
さて,これら式  をゆっくり眺めていると,何となく似ていると思いませんか?何となく似ていると感じた人は,どこがどう似ているのか,よく頭を整理して考えてみて下さい.よく分からない人は,これらの公式で,左辺と右辺がどういう関係で結ばれているのかを,もう一度よく考えてみて下さい.
をゆっくり眺めていると,何となく似ていると思いませんか?何となく似ていると感じた人は,どこがどう似ているのか,よく頭を整理して考えてみて下さい.よく分からない人は,これらの公式で,左辺と右辺がどういう関係で結ばれているのかを,もう一度よく考えてみて下さい.
微分形式
式  はどれも『領域内の変化を領域全体で積分する代わりに,領域の境界での出入りだけを考える』という構造をしていることに気がつきましたか?もちろん,その変化というのが
はどれも『領域内の変化を領域全体で積分する代わりに,領域の境界での出入りだけを考える』という構造をしていることに気がつきましたか?もちろん,その変化というのが 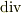 か
か  か
か  かという違いはありますし,積分領域も立体なのか曲面なのか曲線なのかという違いがあります.しかし,これらの定理をまとめて,次のように一つの形に書いてしまうことは可能です.
かという違いはありますし,積分領域も立体なのか曲面なのか曲線なのかという違いがあります.しかし,これらの定理をまとめて,次のように一つの形に書いてしまうことは可能です.

ここで, 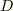 は積分領域,
は積分領域, 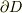 は
は 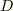 の境界(
の境界( 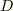 が立体なら
が立体なら 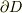 はその表面の曲面,
はその表面の曲面, 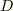 が曲面なら
が曲面なら 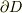 はその周囲の曲線,
はその周囲の曲線, 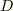 が曲線なら
が曲線なら 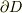 はその始点と終点)を意味するとし,
はその始点と終点)を意味するとし, 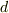 は関数
は関数 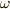 の次元に応じて
の次元に応じて 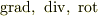 を意味するものとします.そう言われれば,確かに一つの表現にまとめられますが,少し
を意味するものとします.そう言われれば,確かに一つの表現にまとめられますが,少し 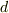 の意味づけに無理があるような気がするかも知れません.実は,ここまで別々に勉強してきた演算
の意味づけに無理があるような気がするかも知れません.実は,ここまで別々に勉強してきた演算 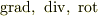 が,一つの演算
が,一つの演算 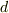 の異なる姿だということが 微分形式 という理論を勉強すると見えてきます.そして, 外積代数 という構造を勉強すると,
の異なる姿だということが 微分形式 という理論を勉強すると見えてきます.そして, 外積代数 という構造を勉強すると, 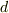 の意味づけが非常に明快になって来ます.今ここでは微分形式の説明はしませんが,ベクトル解析の勉強がだいたい終わったら,次にはこのような分野に進むと面白いと思います.
の意味づけが非常に明快になって来ます.今ここでは微分形式の説明はしませんが,ベクトル解析の勉強がだいたい終わったら,次にはこのような分野に進むと面白いと思います.
| [*] | 補足説明しておきますが,微分形式の理論に出て来る 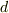 という記号は,外微分と呼ばれるもので, という記号は,外微分と呼ばれるもので, 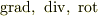 等とまったく同じものではありません.双対外積空間を写像するホッジ作用素というもの考え,外微分と組み合わせることで,これらのベクトル演算子と 等とまったく同じものではありません.双対外積空間を写像するホッジ作用素というもの考え,外微分と組み合わせることで,これらのベクトル演算子と 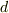 を関係づけることも出来ます.初めて聞く人は,何のこっちゃ!という感じだと思いますが,ゆっくり勉強していきましょう. を関係づけることも出来ます.初めて聞く人は,何のこっちゃ!という感じだと思いますが,ゆっくり勉強していきましょう. 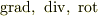 等のベクトル演算子と 等のベクトル演算子と 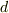 が,そのまんまイコールではないということは頭のどっかに引っ掛けておいて下さい. が,そのまんまイコールではないということは頭のどっかに引っ掛けておいて下さい. |
| [†] | ベクトルの微積分をここまで勉強して来た人は,線積分の向きや,曲面の法線ベクトルの向きなどを小うるさく言うのに少し疲れてきていると思います.一方,いままで 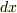 というのは,微積分に出て来る というのは,微積分に出て来る  の微小量という意味の記号で,二乗以上の項を無視するというぐらいしか注意点はありませんでした.微分形式の理論では,微小量 の微小量という意味の記号で,二乗以上の項を無視するというぐらいしか注意点はありませんでした.微分形式の理論では,微小量 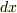 の演算には『向き』の要素も含められていますので,もう悩む必要がありません.さらに の演算には『向き』の要素も含められていますので,もう悩む必要がありません.さらに 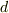 という,単に微小なことを示すだけだった記号に,ベクトル空間の次元を下げるという意味が無理なく与えられて,さらに広い視点で物を見ることが出来るようになっています.さきほど挙げた諸定理の類似性や,極性ベクトルと軸性ベクトルの正体などが,明らかにされます という,単に微小なことを示すだけだった記号に,ベクトル空間の次元を下げるという意味が無理なく与えられて,さらに広い視点で物を見ることが出来るようになっています.さきほど挙げた諸定理の類似性や,極性ベクトルと軸性ベクトルの正体などが,明らかにされます |
| [‡] | 普通の計算をしている限り,微分形式を知らなくてもそれほど困らないと思います.しかし,上で少し見たように,微分形式の理論を使うと,色々なことを統一的に俯瞰できるようになって来ます.例えば,電磁気学の基礎方程式にマックスウェルの方程式と呼ばれるベクトルの方程式があります.マックスウェル(  )が最初, )が最初, 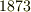 年にこの方程式を考えたとき, 年にこの方程式を考えたとき, 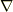 という便利な記号が無かったため, という便利な記号が無かったため, 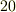 本もの微分方程式に分けて表現されており,今よりもずっと理解し難いものでした.その後,へヴィサイド 本もの微分方程式に分けて表現されており,今よりもずっと理解し難いものでした.その後,へヴィサイド  やギブス やギブス  等がベクトル解析を進歩させた結果,マックスウェルの方程式は 等がベクトル解析を進歩させた結果,マックスウェルの方程式は  本にまとめられ,物理的意味もとても分かりやすい形となりました.(ライプニッツ 本にまとめられ,物理的意味もとても分かりやすい形となりました.(ライプニッツ  が常々言っていた事だそうですが,『数学においては優れた記号が重要だ』という好例だと思います.) が常々言っていた事だそうですが,『数学においては優れた記号が重要だ』という好例だと思います.)  本でも十分に簡単ですが,微分形式を用いれば,マックスウェルの方程式はたった 本でも十分に簡単ですが,微分形式を用いれば,マックスウェルの方程式はたった 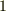 本にまとめてしまうことが可能です.色々なことを洞察する広く深い視点が欲しい方は,ぜひいずれ微分形式に取り組んでみて下さい. 本にまとめてしまうことが可能です.色々なことを洞察する広く深い視点が欲しい方は,ぜひいずれ微分形式に取り組んでみて下さい. |
座標系
また,『  ,
, 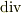 ,
,  は座標系の取り方によらない』『ポテンシャル場の積分は経路によらない』『平面のグリーンの定理は座標変換してもなりたつ』『ストークスの定理は座標系のとりからによらない』など,様々な場面で,座標系の取り方によらない,という事がキーワードになっていました.(平面のグリーンの定理などは,座標系によらない形にするために,わざわざ
は座標系の取り方によらない』『ポテンシャル場の積分は経路によらない』『平面のグリーンの定理は座標変換してもなりたつ』『ストークスの定理は座標系のとりからによらない』など,様々な場面で,座標系の取り方によらない,という事がキーワードになっていました.(平面のグリーンの定理などは,座標系によらない形にするために,わざわざ 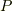 と
と 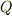 を足してあるのです.)これは,式
を足してあるのです.)これは,式  の公式が何か,座標系という見かけの標構と無縁な,もっと本質的な関係を意味しているということです.ただし,確かに
の公式が何か,座標系という見かけの標構と無縁な,もっと本質的な関係を意味しているということです.ただし,確かに 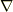 を使って定式化した公式は座標系の取り方に関係しませんが,それは
を使って定式化した公式は座標系の取り方に関係しませんが,それは 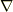 の定義が座標系と無縁だというだけで(確かに,この三角形の記号のどこにも座標系は明記していません),実際に微分演算をする段階では,
の定義が座標系と無縁だというだけで(確かに,この三角形の記号のどこにも座標系は明記していません),実際に微分演算をする段階では, 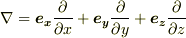 としたり,
としたり, 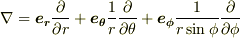 とするなどして,何か座標系を使わないといけないでしょう.このとき
とするなどして,何か座標系を使わないといけないでしょう.このとき 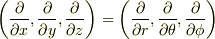 が成り立っている訳ではありませんから,
が成り立っている訳ではありませんから, 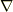 が『座標系の取り方にはよらない』とは言っても,『座標変換に対して不変』ではありません.関数
が『座標系の取り方にはよらない』とは言っても,『座標変換に対して不変』ではありません.関数  の全微分(座標変換に対しても不変)が,座標変換してもそのまま
の全微分(座標変換に対しても不変)が,座標変換してもそのまま  と書けたことを思い出すと,ここで述べた注意点の意味がさらに明快になると思います.そこで,次のレベルを目指す人は『座標系とはそもそも何か』『座標系の取り方による・よらないとはどういうことか』『座標変換にもよらない定式化の仕方はあるのか』といった点を考えることになります.
と書けたことを思い出すと,ここで述べた注意点の意味がさらに明快になると思います.そこで,次のレベルを目指す人は『座標系とはそもそも何か』『座標系の取り方による・よらないとはどういうことか』『座標変換にもよらない定式化の仕方はあるのか』といった点を考えることになります.
微分形式と多様体
先ほどから何度も言及している微分形式の理論を勉強すると,座標系による量と,座標変換しても不変な量の違いがよく見えるようになり,また,今まで別々の計算だと思っていた線積分,面積分,体積分も,統一的に見えてきます.そのような点で,色々な見通しをすっきりと整理してくれる理論です.座標系による量とよらない量の違いは,座標変換の計算が進歩してきた頃から明確に認識されるようになってきたもので,その研究の嚆矢となったのは,近代的な行列の理論の生みの親ともいうべきシルベスター(  )とケーリー(
)とケーリー(  )による不変式の研究でしょう.物理学では,座標系による量は例えば『見かけの力』などと言って,座標系によらない量と区別し,座標系によらない物理量(例えば光速)を,より本質的な量と考えて重宝(?)します.シルベスターとケーリーの研究は,後にテンソルの理論に発展しましたが,テンソルは今や物理学に無くてはならない大事な道具となっています.しかし,テンソルの計算には,添字の扱いがごちゃごちゃと面倒くさいという難点があります.似たような計算を,微分形式を使えばすっきりと表現できたりします.微分形式の理論を最初に発展させたのは,フランスのエリー・カルタン(
)による不変式の研究でしょう.物理学では,座標系による量は例えば『見かけの力』などと言って,座標系によらない量と区別し,座標系によらない物理量(例えば光速)を,より本質的な量と考えて重宝(?)します.シルベスターとケーリーの研究は,後にテンソルの理論に発展しましたが,テンソルは今や物理学に無くてはならない大事な道具となっています.しかし,テンソルの計算には,添字の扱いがごちゃごちゃと面倒くさいという難点があります.似たような計算を,微分形式を使えばすっきりと表現できたりします.微分形式の理論を最初に発展させたのは,フランスのエリー・カルタン(  )です.(息子のアンリ・カルタン
)です.(息子のアンリ・カルタン  も有名な数学者なので,区別するためにフル・ネームで呼びます.)カルタンが最初に微分形式を考えた動機は,微分方程式を本当に座標系に無関係な形で書きたいというものでした.
も有名な数学者なので,区別するためにフル・ネームで呼びます.)カルタンが最初に微分形式を考えた動機は,微分方程式を本当に座標系に無関係な形で書きたいというものでした.

エリー・カルタン.微分形式の理論を一人で発展させた功績は偉大だ.
一方,さらに詳しく座標系を取るということや,座標変換の意味については,多様体という概念によって一般的に説明されます.これについても,また稿を改めて解説したいと思っています.なんだか,微分形式の紹介みたいな記事になってしまいましたが,ベクトルの積分公式に興味を持った人が,今後,どんな勉強をすると理解が深まるか,という道筋を少し提案してみたつもりです.