ガウスの発散定理
ベクトルの面積分に関して, ガウスの発散定理 と呼ばれる重要な定理があります.
theorem
- 【ガウスの発散定理】
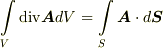
式の変数や積分領域に説明が必要でしょう.左辺は体積分になっていて,  というのがその積分領域です.右辺は面積分になっていて,左辺の積分領域を与える図形の,表面積だけを意味するものです.『発散の体積分が,面積分になってしまう』とは,一体どういうことなのでしょうか?この定理の意味は,物理的・直観的に,よく理解できるものなので,定理を忘れないためにも,まずは簡単に,直観的に考えてみたいと思います.
というのがその積分領域です.右辺は面積分になっていて,左辺の積分領域を与える図形の,表面積だけを意味するものです.『発散の体積分が,面積分になってしまう』とは,一体どういうことなのでしょうか?この定理の意味は,物理的・直観的に,よく理解できるものなので,定理を忘れないためにも,まずは簡単に,直観的に考えてみたいと思います.
| [*] | この定理を,ガウスの定理,ガウスの積分定理などと呼ぶ人もいますが,ガウス  は,あらゆる数学の分野を研究しており,未だに刊行されていない著作集は は,あらゆる数学の分野を研究しており,未だに刊行されていない著作集は  ページを越えるだろうと言われる数学史上最大の超人です.ガウスの定理と言われる定理は無数にあるので,なるべく正確に『ガウスの○○の定理』というように,定理の内容が伝わる名前を使った方が良いと思います.この記事も,そのような理由でガウスの発散定理としました. ページを越えるだろうと言われる数学史上最大の超人です.ガウスの定理と言われる定理は無数にあるので,なるべく正確に『ガウスの○○の定理』というように,定理の内容が伝わる名前を使った方が良いと思います.この記事も,そのような理由でガウスの発散定理としました. |
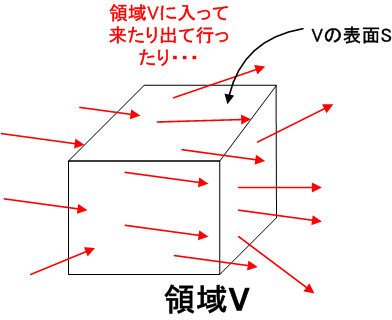
ベクトル場 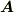 は何かの流れだと考えてください.簡単のため,水の流れだとします.ベクトルの発散は,湧き出しや吸い込みを意味するのでした( div 参照)ので,定理の左辺の意味は『領域
は何かの流れだと考えてください.簡単のため,水の流れだとします.ベクトルの発散は,湧き出しや吸い込みを意味するのでした( div 参照)ので,定理の左辺の意味は『領域 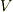 内全体で,新たに増えたり減ったりする流れの総量』を表わすと考えられます.いま,水の圧縮性を考えていませんので,もし,湧き出しや吸い込みが全くなければ,領域
内全体で,新たに増えたり減ったりする流れの総量』を表わすと考えられます.いま,水の圧縮性を考えていませんので,もし,湧き出しや吸い込みが全くなければ,領域 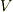 に流入する水量と流出する水量は同じになるはずです.もし湧き出しがあれば,流出する水量の方が多くなり,吸い込みがあれば流入する水量が多くなるはずです.(温泉の湧き出し口か何かをイメージして下さい.)領域
に流入する水量と流出する水量は同じになるはずです.もし湧き出しがあれば,流出する水量の方が多くなり,吸い込みがあれば流入する水量が多くなるはずです.(温泉の湧き出し口か何かをイメージして下さい.)領域 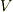 全体での,水量の増減がガウスの発散定理の左辺で意味されているわけです.
全体での,水量の増減がガウスの発散定理の左辺で意味されているわけです.
一方,右辺の中の  は『この領域
は『この領域 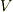 の表面
の表面 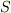 における,
における, 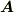 の法線方向成分』だと考えられますので,定理の右辺は『領域の表面
の法線方向成分』だと考えられますので,定理の右辺は『領域の表面 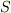 全域に渡る,
全域に渡る, 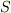 を通過する流れの総量』を表わすものと考えられます.つまり,定理の意味を日本語で再び書くと次のようになります.
を通過する流れの総量』を表わすものと考えられます.つまり,定理の意味を日本語で再び書くと次のようになります.
Important
(領域全体での増減)= (領域表面で出たり入ったりした量の差)
もう一度,最初の式とこの文章を比べて,式の意味をきちんと納得できるまで考えてみて下さい.良い例ではないかも知れませんが,卑近な例としては刑務所を例にとることが出来ます.刑務所に収容されている犯罪者数の増減は,『(新たに入所してくる人数)  (出所していく人数)』で表わすことが出来ます.そして,内部の様子はなかなか調べられませんが,調べたいのが増減だけならば,出入り口だけ調べていれば分かるわけです.ガウスの定理の真髄は,領域内部の 体積分を実行するのが大変場合でも,知りたいのが変化率だけならば,表面の出入りだけを調べることで済ませられる 点にあります.
(出所していく人数)』で表わすことが出来ます.そして,内部の様子はなかなか調べられませんが,調べたいのが増減だけならば,出入り口だけ調べていれば分かるわけです.ガウスの定理の真髄は,領域内部の 体積分を実行するのが大変場合でも,知りたいのが変化率だけならば,表面の出入りだけを調べることで済ませられる 点にあります.
次に,ベクトル場を 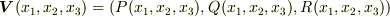 と置いて,ガウスの発散定理の証明を考えます.積分領域
と置いて,ガウスの発散定理の証明を考えます.積分領域 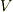 を囲む閉曲面
を囲む閉曲面 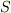 は,表と裏を区別できる曲面だとし,外向きの法線ベクトルを
は,表と裏を区別できる曲面だとし,外向きの法線ベクトルを 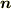 とします.また,次元が分かりやすいように体積分は
とします.また,次元が分かりやすいように体積分は  ,面積分は
,面積分は  のように,積分記号を重ねて書くようにします.
のように,積分記号を重ねて書くようにします.
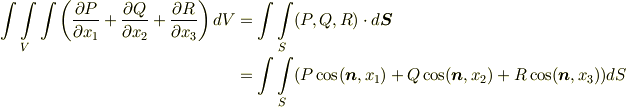
proof
まず, 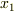 軸から考えます.
軸から考えます. 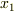 軸に平行な直線は何本でも引けますが,こうした直線のうち,閉曲面
軸に平行な直線は何本でも引けますが,こうした直線のうち,閉曲面 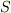 と三点以上で交わるものは無いとします.(つまり,
と三点以上で交わるものは無いとします.(つまり, 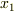 軸と平行で
軸と平行で 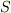 と交わるような直線は,必ず一点(接する)か二点(交接する)で交わるという仮定です.)これら交点のうち,原点に近い側を
と交わるような直線は,必ず一点(接する)か二点(交接する)で交わるという仮定です.)これら交点のうち,原点に近い側を  ,もう一方を
,もう一方を 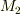 とします(図1を参照).このとき,
とします(図1を参照).このとき, 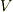 の
の  平面への射影を
平面への射影を 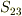 とすると,体積分の
とすると,体積分の 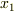 軸方向成分は,
軸方向成分は, ![\int \int \int \limits _{V} \frac{\partial P}{\partial x_{1}}dV= \int \int \limits _{S_{23}} \left( \int \frac{\partial P}{\partial x_{1}}dx_{1} \right) dS_{23} = \int \int \limits _{S_{23}} [P(M_{2})-P(M_{1})] dS_{23}](./8e10d08552ce72661921f09a7597ab13.png) と表わせます.( 面積分と体積分 で考えた形です.)ここで,面積素
と表わせます.( 面積分と体積分 で考えた形です.)ここで,面積素 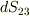 は,点
は,点 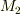 における曲面
における曲面 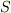 の面積素
の面積素 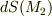 の射影として表現できます.
の射影として表現できます. 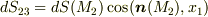 .(点
.(点  における面積素
における面積素 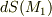 の射影も同様ですが,点
の射影も同様ですが,点  では法線ベクトルの向きが
では法線ベクトルの向きが 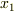 軸の向きと逆になるため,
軸の向きと逆になるため, 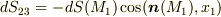 のようにマイナスがつくことに注意して下さい.)これより
のようにマイナスがつくことに注意して下さい.)これより 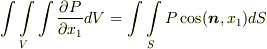 が言えます. 全く同様に
が言えます. 全く同様に 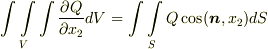 ,
, 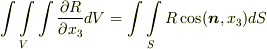 も言えるので,これらの式の辺々を足して定理が示されます.■
も言えるので,これらの式の辺々を足して定理が示されます.■
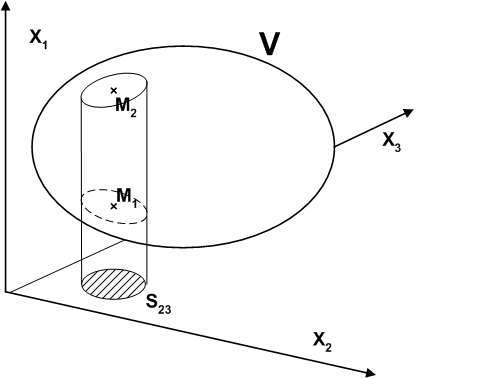
図1
結局,証明では,各成分毎に 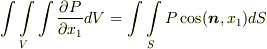 のような形を考え,最後に三つ足すだけになっています.これら個別の関係式は 面積分と体積分 で考えたものです.しかし,各成分毎に成り立っている式を,単に辺々足し合わせているだけならば『なぜ成分毎の公式にしないのか?必要な時に足し合わせればいいんだから,その方が細かく使えていいじゃないか.』と思う人がいるかも知れません.ガウスの発散定理が各成分の式を足した形になっているのは,この形が 座標系によらない からです.つまり,もし
のような形を考え,最後に三つ足すだけになっています.これら個別の関係式は 面積分と体積分 で考えたものです.しかし,各成分毎に成り立っている式を,単に辺々足し合わせているだけならば『なぜ成分毎の公式にしないのか?必要な時に足し合わせればいいんだから,その方が細かく使えていいじゃないか.』と思う人がいるかも知れません.ガウスの発散定理が各成分の式を足した形になっているのは,この形が 座標系によらない からです.つまり,もし 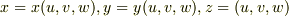 と表わせるとして,変数を
と表わせるとして,変数を 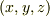 から
から 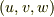 に変換したとしても,ガウスの発散定理はやはり成り立つのです.これは非常に美しい結果ですし,座標成分という勝手に取った標構の向こうに,何か不動の本質的な物が見え隠れしているように思えてきます.ガウスの発散定理の座標不変性については 微分形式 で詳しく考える予定です.当面はとりあえず,座標不変というキーワードだけを覚えておいて下さい.
に変換したとしても,ガウスの発散定理はやはり成り立つのです.これは非常に美しい結果ですし,座標成分という勝手に取った標構の向こうに,何か不動の本質的な物が見え隠れしているように思えてきます.ガウスの発散定理の座標不変性については 微分形式 で詳しく考える予定です.当面はとりあえず,座標不変というキーワードだけを覚えておいて下さい.
| [†] | 証明の中で, 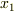 軸に平行な直線は曲面 軸に平行な直線は曲面 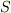 と二箇所以上では交わらないと仮定しました.これは,位相的に言えば,領域 と二箇所以上では交わらないと仮定しました.これは,位相的に言えば,領域 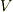 の中に描いた輪を縮めていくとき,輪をどこに取っても一点にまで縮められるということです.ただし,この条件は外すことも出来ます.領域 の中に描いた輪を縮めていくとき,輪をどこに取っても一点にまで縮められるということです.ただし,この条件は外すことも出来ます.領域 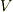 の中に,空洞(大根の鬆を想像してください)が幾つかあっても, の中に,空洞(大根の鬆を想像してください)が幾つかあっても, 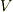 を幾つかの小領域に分割し,それぞれに対してガウスの発散定理を適用することで,全体としてもガウスの発散定理が成り立つことが示せます.隣同士で接している小領域では,接している面での面積分が相殺するからです. を幾つかの小領域に分割し,それぞれに対してガウスの発散定理を適用することで,全体としてもガウスの発散定理が成り立つことが示せます.隣同士で接している小領域では,接している面での面積分が相殺するからです. |
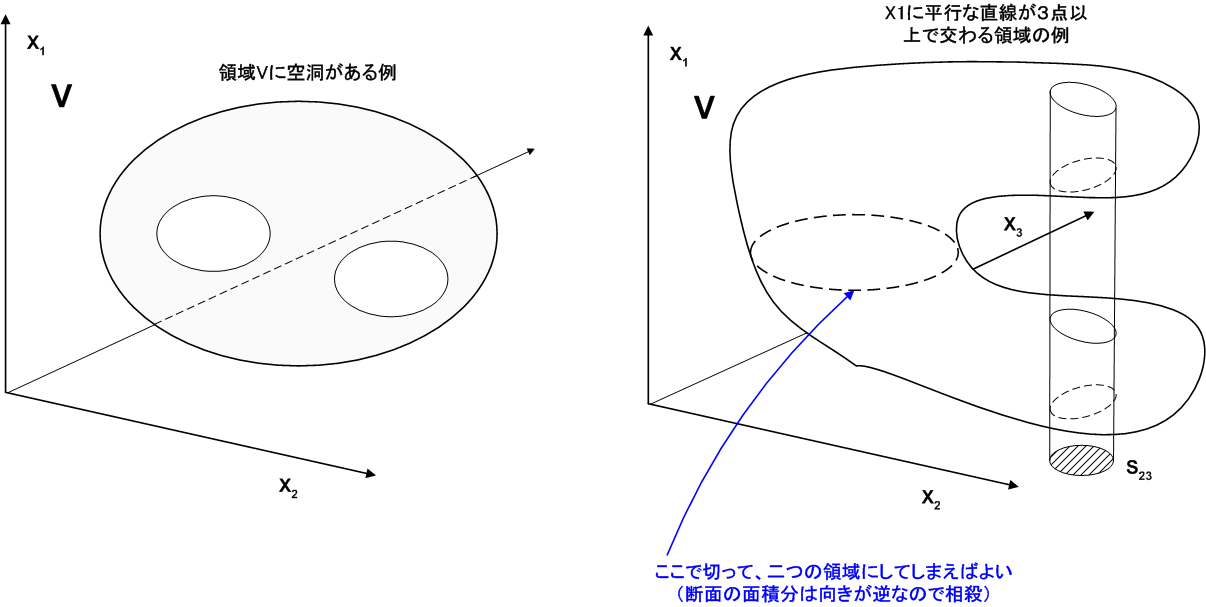
図2
| [‡] | ここまでは,暗黙のうちに曲面 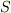 は十分滑らかだとしていましたが,区分的に滑らかとしても定理は成り立ちます.区分的に滑らかと言うのは,幾つか尖がった点があっても良いということです.三角柱や円筒など,普通の形の領域には,たいていガウスの発散定理が安心して使えます. は十分滑らかだとしていましたが,区分的に滑らかとしても定理は成り立ちます.区分的に滑らかと言うのは,幾つか尖がった点があっても良いということです.三角柱や円筒など,普通の形の領域には,たいていガウスの発散定理が安心して使えます. |