ストークスの定理
ガウスの定理,平面のグリーンの定理などと並んで,ベクトル解析分野で最も重要な積分定理が,この ストークスの定理 です.ストークスの定理は,三次元の曲面とその曲面上で定義された関数に関し,線積分と面積分を関係づける定理です.
theorem
【ストークスの定理】閉曲線 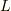 を境界とする曲面
を境界とする曲面  上で,
上で,  級ベクトル値関数
級ベクトル値関数 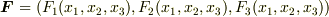 が定義されています.ただし
が定義されています.ただし  は単連結とします.このとき
は単連結とします.このとき 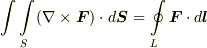 が成り立ちます.
が成り立ちます.
まず,証明を考えてみますが,あまり数学的に細かいことよりは,まず物理的・直観的なイメージで定理の意味を把握する事が重要だと思います.(単連結という言葉の意味が分からない人がいると思いますが, 積分領域について補足 で説明しますので,今はこだわらなくて良いです.)直観的説明は次のセクションで考察します.細かいことを気にしない人は,とりあえず証明を飛ばしてしまっても良いと思います.曲面  は表裏のある曲面とし,法線ベクトル
は表裏のある曲面とし,法線ベクトル 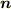 は
は  の表側を向く方向を正とします.線積分の回る向きは,
の表側を向く方向を正とします.線積分の回る向きは,  の表側を左手に見ながら一周する向きとします.( 平面のグリーンの定理 で強調したように,周回積分では常に向きが非常に重要です.)また,
の表側を左手に見ながら一周する向きとします.( 平面のグリーンの定理 で強調したように,周回積分では常に向きが非常に重要です.)また,  級関数というのは,少なくとも一階導関数が滑らかだという意味です.
級関数というのは,少なくとも一階導関数が滑らかだという意味です.
proof
まず, 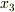 軸に平行で
軸に平行で  を通る直線は,三つ以上の交点は持たないものとします.(ただし,この仮定は積分領域を分割することで外すことが可能です.後述します.)曲面
を通る直線は,三つ以上の交点は持たないものとします.(ただし,この仮定は積分領域を分割することで外すことが可能です.後述します.)曲面  を
を 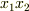 平面に射影した領域を
平面に射影した領域を 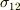 とし,曲線
とし,曲線 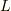 を
を 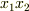 平面に射影した領域を
平面に射影した領域を 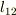 とします.また空間曲線
とします.また空間曲線 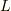 は,
は, 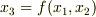 と表現されるとします.すると,線積分は
と表現されるとします.すると,線積分は 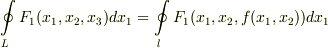 と変形できます.さらに
と変形できます.さらに 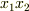 平面上で 平面のグリーンの定理 を適用すると
平面上で 平面のグリーンの定理 を適用すると  が成り立ちます.そこで,
が成り立ちます.そこで,  に関する線積分に戻して
に関する線積分に戻して 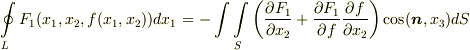 を得ます.ここで,
を得ます.ここで, 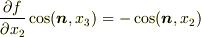 が成り立ちますので(あとで補足説明します),
が成り立ちますので(あとで補足説明します),  を得ます.同様に
を得ます.同様に 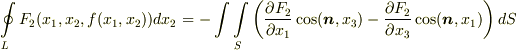 ,
, 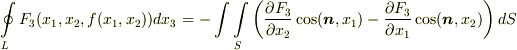 が成り立ちます.これら三式を辺々足すことで定理が示されます.■
が成り立ちます.これら三式を辺々足すことで定理が示されます.■
途中で 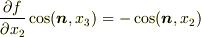 という関係を使いましたが,これは次の関係式から導けます.法線ベクトルが
という関係を使いましたが,これは次の関係式から導けます.法線ベクトルが  で表現されることは grad を参照して下さい.
で表現されることは grad を参照して下さい.
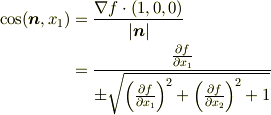
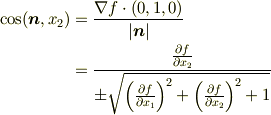
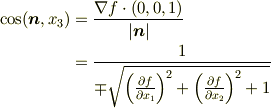
また, 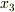 軸に平行で
軸に平行で  を通る直線は,三つ以上の交点は持たないと証明の最初で仮定しましたが,この仮定を満たさない領域でも,より単純な小領域に分割することでストークスの定理を適用することが出来ます.(この考え方は, ガウスの発散定理 や 平面のグリーンの定理 でも用いましたので,参照して下さい.)結論として,
を通る直線は,三つ以上の交点は持たないと証明の最初で仮定しましたが,この仮定を満たさない領域でも,より単純な小領域に分割することでストークスの定理を適用することが出来ます.(この考え方は, ガウスの発散定理 や 平面のグリーンの定理 でも用いましたので,参照して下さい.)結論として,  が 区分的に滑らか であれば(つまり,尖がった点がせいぜい有限個くらいしか無い形ならば),ストークスの定理を適用することが可能です.これはかなり緩やかな条件ですから,実質的には,物理の問題に出て来るほとんどの曲面に対してストークスの定理が使えます.
が 区分的に滑らか であれば(つまり,尖がった点がせいぜい有限個くらいしか無い形ならば),ストークスの定理を適用することが可能です.これはかなり緩やかな条件ですから,実質的には,物理の問題に出て来るほとんどの曲面に対してストークスの定理が使えます.
| [*] | 証明の最後で,別々に成り立っている三つの式を足し合わせています.全く同じ手順が 平面のグリーンの定理 や ガウスの発散定理 の証明でも取られていました.もう感ずいていると思いますが,わざわざ三つの式を一まとめにした形を定理として覚えておきたい理由は,ストークスの定理が座標系の取り方によらずに成り立つからです. |
| [†] | ストークスの定理の積分領域は,単連結という形であることが非常に重要ですが,このことについては 積分領域について補足 で勉強します.とりあえず,先ほど図で考えたような,単純な切れ目の無いの曲面に関する限り,ストークスの定理は成り立つと考えておいて下さい. |
ストークスの定理の直観的理解
ストークスの定理の意味を,もう少し直観的に考えてみましょう.定理に対して生き生きとしたイメージを持っていると,忘れにくく,応用的に使うことができるようになります.
まず,左辺の 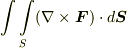 ですが,
ですが,  が局所的な回転を意味していることは, rot で勉強しました.
が局所的な回転を意味していることは, rot で勉強しました.
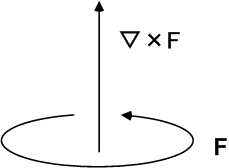
曲面  上の各点で定義される局所的な回転を,
上の各点で定義される局所的な回転を,  全面に渡って足し合わせてしまうというのが積分の意味ですから,イメージとしては,次図のような感じですね.(図では
全面に渡って足し合わせてしまうというのが積分の意味ですから,イメージとしては,次図のような感じですね.(図では  を格子状に区切って,長方形領域に書いていますが,格子の数を
を格子状に区切って,長方形領域に書いていますが,格子の数を 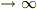 ,格子の面積を
,格子の面積を  と極限を取ることで正確に積分の計算になります.)
と極限を取ることで正確に積分の計算になります.)
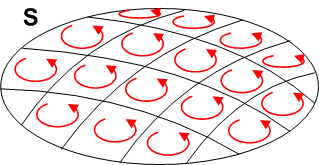
ここで,隣り合う領域では,その境界で回転の向きが逆になりますので,互いに打ち消しあってしまい,結局,一番外側の 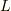 に沿った回転しか残らないことになります.
に沿った回転しか残らないことになります.
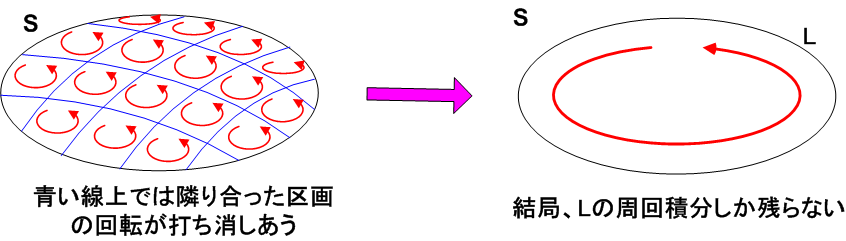
これは, 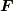 を
を 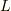 に沿って周回積分したもの
に沿って周回積分したもの 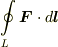 ですから,ストークスの定理
ですから,ストークスの定理 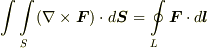 が成り立ちます.曲面
が成り立ちます.曲面  を格子状に区切り,隣り合う領域の回転が互いに打ち消し合うというイメージを持てていれば,ストークスの定理の意味は明快ですし,定理も忘れないと思います.
を格子状に区切り,隣り合う領域の回転が互いに打ち消し合うというイメージを持てていれば,ストークスの定理の意味は明快ですし,定理も忘れないと思います.
演習問題1
実際に計算してストークスの定理を確認してみましょう.原点を中心とする単位球面 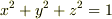 が平面
が平面 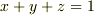 で切られるとき,その原点から遠い側の曲面を
で切られるとき,その原点から遠い側の曲面を  ,
,  の縁を
の縁を 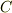 とします.このとき,
とします.このとき, 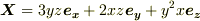 して,
して, 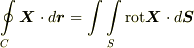 を確認してください.
を確認してください.
(ヒント:面積分をするには,まず一変数消去して  をうまく二変数で表し,
をうまく二変数で表し,  を表わしてみましょう.)
を表わしてみましょう.)