続×4ベクトルの回転
我々は, 続々ベクトルの回転 で行列の指数関数がうまく行列の回転を 表すことを見ました.それはなぜかを説明できたので, 解釈の仕方を書こうと思います.
回転を表す微分方程式
Joh氏は ベクトルの回転 に於いて,微小回転について触れています. それは次のような式です.

ここで,この微小量を時間 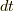 での微分と考えて,
での微分と考えて,  と置くと,
と置くと,
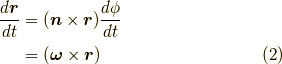
とします.これは単位時間に回転軸 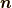 と回転の対象である位置ベクトル
と回転の対象である位置ベクトル  の両方に直交する
方向に
の両方に直交する
方向に 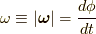 だけ動く系であることを示しています.
つまり,その解
だけ動く系であることを示しています.
つまり,その解  は回転を行った後の位置ベクトルを記述します.
は回転を行った後の位置ベクトルを記述します.
ここで 続ベクトルの回転 で書いた行列での記法で,式  を書き直します.
すると,
を書き直します.
すると,
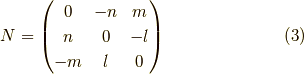
と行列で表現できますから,式  は,
は,

となります.すると, ジョルダン標準形の指数関数の応用 と同じ論法で,解は

だと分かります.なぜこうなるかは,次の話が厳密ではありませんが参考にはなるでしょう.
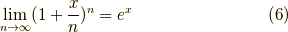
がネイピア数の定義だったと思います.
ここで微小回転を  に施すということは,
に施すということは,

ということでした.これを二ステップに分けて考えると,
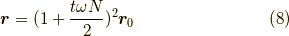
となり,三ステップだと,
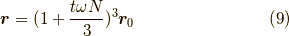
ですね?つまり, それを何回も分けて繰り返すと,
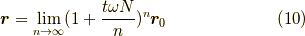
と書いてよいでしょう.つまり,これは
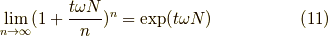
ということです.
Nの指数関数の計算
これから,もうすでに 続々ベクトルの回転 で求めましたが,
別の方法で行列  の指数関数を求めたいと思います.まず,
の指数関数を求めたいと思います.まず,  を対角化して
を対角化して  とし,
とし,  の
の  乗を求めます.
乗を求めます.
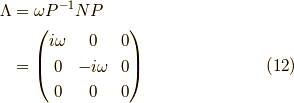
で,この固有値の順番に対応する固有ベクトルからなる行列 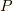 は,
は,
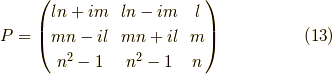
となります. 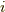 は虚数単位です.
よって,この行列の指数関数は,
は虚数単位です.
よって,この行列の指数関数は,
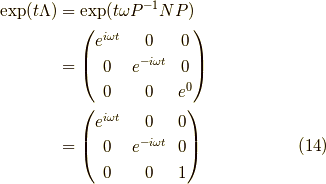
となります.
ここで後の議論に便利なように, 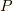 をユニタリー化して
をユニタリー化して  としておきます.
なぜなら,そうすると逆行列が共役転置(随伴作用)で求まるからです.
簡単の為,三次元極座標
としておきます.
なぜなら,そうすると逆行列が共役転置(随伴作用)で求まるからです.
簡単の為,三次元極座標
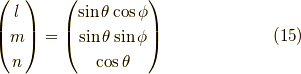
を導入すると,
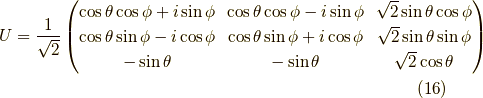
であり,この共役転置行列 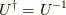 は,
は,
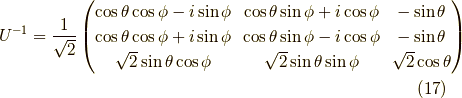
です.よって,ダイアド積 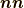 を用いて,
を用いて,
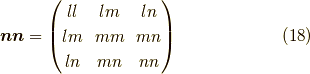
と書き,三次単位行列を 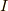 と書くことにすると, 正方行列の三連続積の展開 の方法を用いて,
と書くことにすると, 正方行列の三連続積の展開 の方法を用いて,
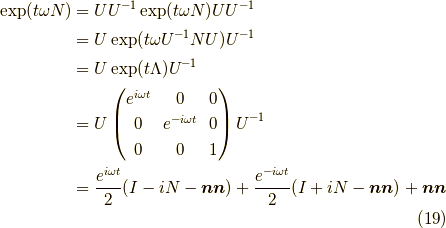
ここで,
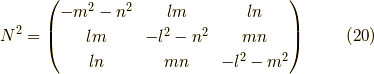
なので,

の関係を使うと,

となり, 続々ベクトルの回転 の結果と一致します.
つまり,これは位置ベクトルが回転軸  の周りを角速度
の周りを角速度  で回転する様子を
記述している式だったのです.めでたしめでたし.
で回転する様子を
記述している式だったのです.めでたしめでたし.
2023.11.11追記
この議論は  の議論に引きずられていて,最後の結論がおかしいです.
の議論に引きずられていて,最後の結論がおかしいです.

となるはずです.原因が分かりませんが,ご注意だけ,すみません.
それでは,今日はこの辺で,お疲れ様でした.