ジョルダン標準形の指数関数の応用
我々は ジョルダン細胞のn乗 に於いて,行列の指数関数を 考えましたが,今回の話はその応用例です.
一次連立微分方程式
どんな正方行列 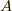 も複素数の範囲でジョルダン標準形
も複素数の範囲でジョルダン標準形 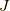 を持ちます.
(運が良い時には対角行列になります.)
つまり,固有ベクトル(正確にはジョルダン基底というようです.
掲示板でご指摘いただきました.数学男子さんに感謝です^_^.
)を並べた正則行列を
を持ちます.
(運が良い時には対角行列になります.)
つまり,固有ベクトル(正確にはジョルダン基底というようです.
掲示板でご指摘いただきました.数学男子さんに感謝です^_^.
)を並べた正則行列を 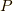 と置くと,
と置くと,

となります.ここで次の連立方程式の解を求めることにこの事実を応用できます.
n次列ベクトルを 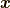 と置くと,
と置くと,

です.式  に左から
に左から 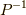 を掛けると,
を掛けると, 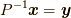 と置くと,
と置くと, 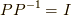 で単位行列ですから,
で単位行列ですから,

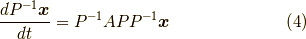

となり, 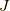 はまさにジョルダン標準形です.
ここで初期状態を
はまさにジョルダン標準形です.
ここで初期状態を 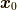 とし,対応する
とし,対応する  を
を 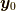 とします.
すると,少し天下り的ですが,解は次のようになります.(行列の指数関数
とします.
すると,少し天下り的ですが,解は次のようになります.(行列の指数関数 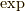 については 続々ベクトルの回転
をご覧ください.)
については 続々ベクトルの回転
をご覧ください.)

この式は微分すると,確かに
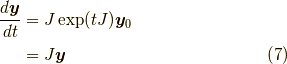
となっていますね.こういう視点で考えると実は ベクトルの回転 は 新しい見方ができます.それは, 続4ベクトルの回転 で扱います.
それでは今日はこの辺で. お疲れ様でした.