続・ベクトルの回転
これは,Joh氏の ベクトルの回転 の記事の続編です. 次の記事は, 続々ベクトルの回転 です. 行列の回転を三次正方行列で表すと,意外ときれいな形でまとまったので書いてみました.
ベクトルの回転の行列表現
これから ベクトルの回転 で出た式を行列で表します.ではさっそく元の式を見てみましょう.
![\bm{r}^\prime = (\bm{n} \cdot \bm{r}) \bm{n} + [\bm{r}-(\bm{n} \cdot \bm{r})\bm{n}]\cos \phi +(\bm{n} \times \bm{r})\sin \phi \tag{1}](./d78477fc65be68dceb7e1666ffb7f36f.png)
ここで 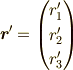 と
,
と
, 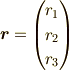 として
,
として
, 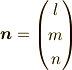 とすると,
とすると,
![\begin{pmatrix} r_1^\prime \\ r_2^\prime \\ r_3^\prime \end{pmatrix}=\left[ \bm{n} \bm{n} + \cos \phi (I-\bm{n}\bm{n}) + \sin \phi \begin{pmatrix}0 & -n & m \\n & 0 & -l \\-m & l & 0 \end{pmatrix} \right]\begin{pmatrix} r_1 \\ r_2 \\ r_3 \end{pmatrix}](./4bbe987ce7c979ae059e45dcaa56d942.png)
ここで, 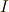 は三次正方単位行列,
また
は三次正方単位行列,
また 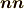 は
は 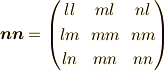 となっていて
これをテンソルと考えた時,ダイアド積(別名として「テンソル積」単に「ダイアド」とも)と呼びます.
となっていて
これをテンソルと考えた時,ダイアド積(別名として「テンソル積」単に「ダイアド」とも)と呼びます.
ダイアド積は,ドットでもクロスでもなくただベクトルを並べるだけで表し,二階のテンソルの表現の一種です
. 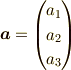 と
と
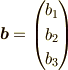 に対し,ダイアド積
に対し,ダイアド積 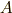 は,
は,
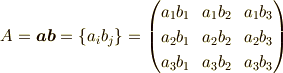
となります.
そして少ししつこいかもしれませんが,
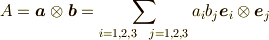
とも書きます.
ところで, 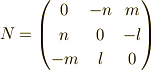 と置くと,
と置くと,
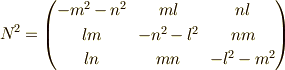 より,
なんと
より,
なんと
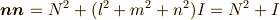
となります.よって,最終的に次の形になります.
![\bm{r}^\prime = [I + N^2 + (-\cos \phi N^2+\sin \phi N)]\bm{r}](./30d7c043d6832bea1b32ffa9e9edcfc8.png)
ここで, 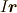 は回転前のベクトル.他は,
は回転前のベクトル.他は, 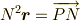 であり
,
であり
, 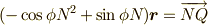 です.
です.
その他の嬉しいこと
余談ですが結構物理では外積 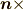 の行列表現
の行列表現 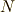 は
もちろん
は
もちろん 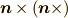 の行列表現
の行列表現 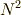 の形をしたものを目にすることが多いと思います.
例えば遠心力は
の形をしたものを目にすることが多いと思います.
例えば遠心力は 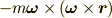 という形をしていますし,
慣性テンソル
という形をしていますし,
慣性テンソル 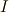 を求める時,角運動量
を求める時,角運動量 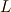 ,角速度ベクトル
,角速度ベクトル 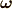 として,
として,
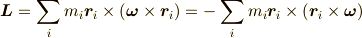
に対して,
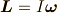
が 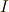 の定義ですから,
の定義ですから,
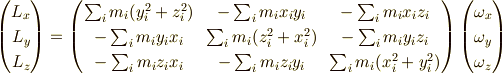
これを知っていると戸惑うことはなくなると思います.
電磁気学でも
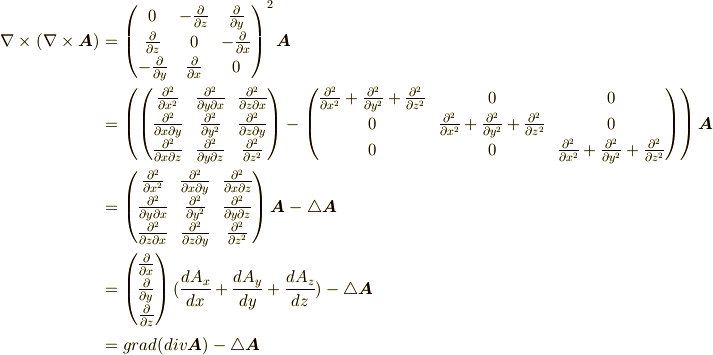
という公式が少し考えるだけで書けるようになります.
追記:最後の電磁気学の例は,偏微分が交換できる時に限るようです.