反対称テンソルと軸性ベクトル
反対称テンソルとは,テンソルの成分の添字をどれか一つ入れ替えると全体の符号が逆になるものを意味しました.
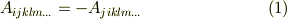
二階のテンソルで例を考えると,次のような行列で表現されるテンソルは反対称テンソルになります.
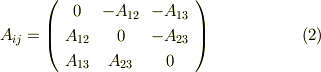
この記事では,反対称テンソルと軸性ベクトルの関係を探ります.軸性ベクトルの定義は, 軸性ベクトルと極性ベクトル を参照して下さい.
反対称テンソルの座標変換
二階の反対称テンソルを例に,テンソルの座標変換の式 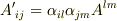 を反対称テンソルについて考えます.
を反対称テンソルについて考えます.
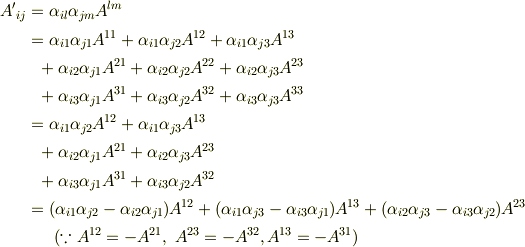
縮約を使って右辺をまとめると,結局,反対称テンソルの座標変換の式は次の形に表現できることが分かります.
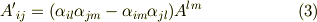
しかし,行列表現 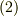 を見れば一目瞭然ですが,反対称テンソルの成分に独立なものは
を見れば一目瞭然ですが,反対称テンソルの成分に独立なものは 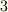 つしかありませんから,添字が二つもついた
つしかありませんから,添字が二つもついた 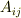 の表記は少し大袈裟に見えます.(成分の計算だけなら
の表記は少し大袈裟に見えます.(成分の計算だけなら  とすれば十分そうです.)そこで,式
とすれば十分そうです.)そこで,式 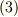 の表記をさらに簡単化する可能性を探ってみましょう.
の表記をさらに簡単化する可能性を探ってみましょう.
直交座標の場合
結論から言うと,基底が正規直交座標系の場合に式 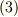 をさらに簡単にできます.そのため,まず適当な基底の座標変換
をさらに簡単にできます.そのため,まず適当な基底の座標変換 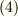 を考えます.(直交座標系の場合,共変基底と反変基底の区別は無くなりますので,このセクションの添字は全て右下に書くことにします.)この後の式変形は,式
を考えます.(直交座標系の場合,共変基底と反変基底の区別は無くなりますので,このセクションの添字は全て右下に書くことにします.)この後の式変形は,式 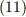 に至るまで,少しトリッキーです.何をやっているのか分からない部分があるかも知れませんが,頑張って一行ずつ追ってみて来てください.
に至るまで,少しトリッキーです.何をやっているのか分からない部分があるかも知れませんが,頑張って一行ずつ追ってみて来てください.

式 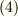 の両辺と
の両辺と  の外積を取り,次式を得ます.
の外積を取り,次式を得ます.
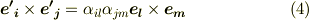
さらに 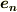 と両辺の内積を取ります.
と両辺の内積を取ります.
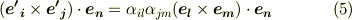
何がしたかったかと言うと,スカラー三重積の形を作りたかったのです.ここで, 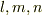 は巡回的だとすると,右辺の
は巡回的だとすると,右辺の 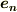 の添字
の添字  を
を 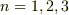 と動かすとき,
と動かすとき, 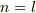 や
や  となる場合は
となる場合は 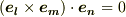 となってしまいます( 三重積 参照)ので,右辺には
となってしまいます( 三重積 参照)ので,右辺には 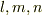 が相異なる場合の項しか残らないことになります.
が相異なる場合の項しか残らないことになります. 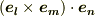 と
と  を区別して,右辺に残るのは二項だけです.
を区別して,右辺に残るのは二項だけです.
では 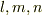 は相異なるとして,右辺の三重積は具体的にどうなるかと言えば,いま基底
は相異なるとして,右辺の三重積は具体的にどうなるかと言えば,いま基底 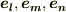 は正規直交座標系だと考えていますので,
は正規直交座標系だと考えていますので, 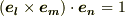 となります.(
となります.( 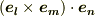 は基底
は基底 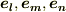 が張る平行六面体の体積でした.)これらの結果を考慮すると,式
が張る平行六面体の体積でした.)これらの結果を考慮すると,式 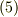 は次のようになります.
は次のようになります.
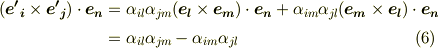
次に,左辺をもう少し工夫することを考えましょう.左辺の添字 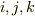 も巡回的であるとすると,座標変換後の新しい正規直交系の基底
も巡回的であるとすると,座標変換後の新しい正規直交系の基底 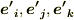 について,右手系の正規直交基底ならば式
について,右手系の正規直交基底ならば式  ,左手系の正規直交基底ならば式
,左手系の正規直交基底ならば式 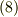 がなりたつことが言えます.これは外積の定義です.
がなりたつことが言えます.これは外積の定義です.


そこで,左辺は  と変形できるでしょう.ダッシュのついた座標系をこのように取ると,式
と変形できるでしょう.ダッシュのついた座標系をこのように取ると,式 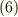 をさらに次式のように簡単化できます
.
をさらに次式のように簡単化できます
. 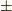 は右手系か左手系かに応じて決めるものとします.
は右手系か左手系かに応じて決めるものとします.
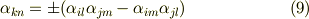
式 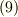 に含まれる添字は,
に含まれる添字は, 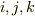 と
と 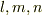 がそれぞれ巡回的である点に注意してください.ここでもう一度,式
がそれぞれ巡回的である点に注意してください.ここでもう一度,式 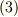 を眺めてみましょう.ただし,添字は全て下付きとします.
を眺めてみましょう.ただし,添字は全て下付きとします.
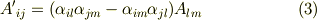
反対称テンソルでは,独立な成分は 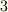 つしかありませんでしたので,
つしかありませんでしたので, 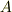 の添字の数を一個にして
の添字の数を一個にして 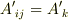 ,
,  (
( 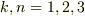 )と置いても一般性を失いません.
)と置いても一般性を失いません.
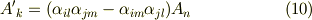
右辺に式 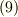 の結果を代入すると,次式に至ります.これが,求めていた反対称テンソル成分の座標変換の式になります.
の結果を代入すると,次式に至ります.これが,求めていた反対称テンソル成分の座標変換の式になります.

式 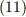 は見かけ上,ベクトルの座標変換の式によく似ていますが,今まで知っていたベクトルの座標変換式と少し違って,
は見かけ上,ベクトルの座標変換の式によく似ていますが,今まで知っていたベクトルの座標変換式と少し違って, 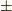 という余計な記号がついています.これは途中でも説明しましたが,右手系から右手系もしくは左系から左手系への座標変換に際しては
という余計な記号がついています.これは途中でも説明しましたが,右手系から右手系もしくは左系から左手系への座標変換に際しては  ,右手系から左手系もしくは左手系から右手系への座標変換では
,右手系から左手系もしくは左手系から右手系への座標変換では  に取るように定められる符号です.
に取るように定められる符号です.  や
や 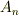 はベクトルのように見えますが, テンソルの概念 で与えた一階のテンソルの定義
はベクトルのように見えますが, テンソルの概念 で与えた一階のテンソルの定義 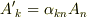 と異なりますので,ベクトルとは少し違う量のようです.
と異なりますので,ベクトルとは少し違う量のようです.
『少し違う』という意味で,座標変換に際して式 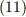 に従う量を 擬ベクトル と呼びます.より一般に高階のテンソルについても,座標変換に際して座標系の取り方(右手系か左手系か)を入れ替えるとき,成分の符号が変わるものを 擬テンソル と呼びます.すでに 軸性ベクトルと極性ベクトル で考えた軸性ベクトルとは,擬ベクトルの別名でもあると言えます.
に従う量を 擬ベクトル と呼びます.より一般に高階のテンソルについても,座標変換に際して座標系の取り方(右手系か左手系か)を入れ替えるとき,成分の符号が変わるものを 擬テンソル と呼びます.すでに 軸性ベクトルと極性ベクトル で考えた軸性ベクトルとは,擬ベクトルの別名でもあると言えます.
二階の反対称テンソルは,擬ベクトル(軸性ベクトル)と等価であることが分かりました.一般の擬テンソルについては, 擬テンソル でもう少し詳しく勉強します.