テンソルの概念
ここまでにもテンソルという言葉はちょくちょく出てきましたが,いよいよテンソルの勉強を始めます.添字を使ったベクトルの扱いに慣れていれば,テンソルの計算そのものはそれほど難しくありません.
復習のため,まずスカラーから話を始めます.スカラーとは座標系によらない量ですから,例えば 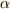 がスカラーだとすると,どの座標系から見ても
がスカラーだとすると,どの座標系から見ても 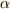 は
は 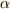 です.
です. 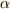 には添字も何も付きません.添字の数は
には添字も何も付きません.添字の数は 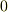 です.ふむふむφ(..)
です.ふむふむφ(..)
次にベクトルを思い出しましょう.ベクトルはある座標系の上で  のように書けました.
のように書けました. 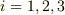 と略して,
と略して, 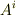 と書くことができますので,添字の数は
と書くことができますので,添字の数は 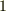 です.ベクトルの成分は,座標系に応じて変化します.
です.ベクトルの成分は,座標系に応じて変化します.
最後に, 計量テンソル の記事に出てきた計量テンソル 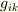 を考えてみます.計量テンソルは次式のようにベクトルをベクトルに変換するものとして定義されていましたが,名前の通りテンソルです.添字の数は見ての通り
を考えてみます.計量テンソルは次式のようにベクトルをベクトルに変換するものとして定義されていましたが,名前の通りテンソルです.添字の数は見ての通り  です.
です.
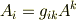
添字の数が 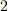 なので,計量テンソルは 二階のテンソル という種類になります.実は スカラーは零階のテンソル , ベクトルは一階のテンソル なのです.二階のテンソル成分もベクトル同様,座標系に応じて値が変化し,添字の上下によって 共変テンソル , 反変テンソル などの違いがあります.さらに,上下の添字両方を含むものを 混合テンソル と呼びます.(詳しくは テンソルの一般的表現 を参照してください.)
なので,計量テンソルは 二階のテンソル という種類になります.実は スカラーは零階のテンソル , ベクトルは一階のテンソル なのです.二階のテンソル成分もベクトル同様,座標系に応じて値が変化し,添字の上下によって 共変テンソル , 反変テンソル などの違いがあります.さらに,上下の添字両方を含むものを 混合テンソル と呼びます.(詳しくは テンソルの一般的表現 を参照してください.)
添字の数に注目して,スカラー,ベクトル,二階のテンソルと順番に見てみましたが,どうやらテンソルとはベクトルの概念をさらに拡張したもののようですね.
変換則
スカラー 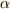 ,ベクトル
,ベクトル 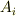 ,計量テンソル
,計量テンソル 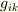 の添字の数は,それぞれ
の添字の数は,それぞれ  でした.添字の数がもっと多い量
でした.添字の数がもっと多い量 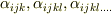 も,いくらでも考えることができます.これらをまとめて テンソル と呼びます.添字の数を明示的に示すためには,添字の数で
も,いくらでも考えることができます.これらをまとめて テンソル と呼びます.添字の数を明示的に示すためには,添字の数で  階のテンソルと呼ぶのが正確です.
階のテンソルと呼ぶのが正確です.
ここまでに,計量テンソル(二階のテンソル),スカラー(零階のテンソル),ベクトル(一階のテンソル)は勉強しましたが,一般に  階のテンソルと言えば,添字が
階のテンソルと言えば,添字が  個ついた量になります.
個ついた量になります.
では,単に添字がたくさんついた量をテンソルと呼ぶのかと言えば,そうではありません.テンソルの満たす大事な性質に, 変換則 にあります.
ある座標系 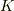 から,新しい座標
から,新しい座標 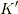 に座標変換することを考えます.ここで行う座標変換は,ベクトルの長さを変えない変換とします.言い方を変えて,内積の値を変えない変換と言っても同じことです.( 内積空間 参照.)具体的には,これは平行移動と回転からなる変換になり,このような変換を総じて 直交変換 と呼びます.
に座標変換することを考えます.ここで行う座標変換は,ベクトルの長さを変えない変換とします.言い方を変えて,内積の値を変えない変換と言っても同じことです.( 内積空間 参照.)具体的には,これは平行移動と回転からなる変換になり,このような変換を総じて 直交変換 と呼びます.
直交変換に際して,スカラー,ベクトル,二階のテンソル,三階のテンソル,そして  階のテンソルが,どうような変換をされるかを例示します.
階のテンソルが,どうような変換をされるかを例示します.


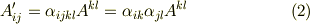
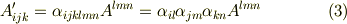

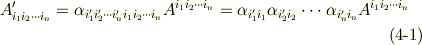
両辺の添字の関係に着目して下さい. 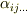 は
は  を変換する働きをしていますが,右辺で上下に分かれて現われた添字を消すと,形式的に左辺の形になることを確認して下さい.また,添字の数に注意すると,
を変換する働きをしていますが,右辺で上下に分かれて現われた添字を消すと,形式的に左辺の形になることを確認して下さい.また,添字の数に注意すると,  階のテンソル
階のテンソル 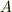 が,
が,  階のテンソル
階のテンソル 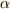 によって
によって  階のテンソル
階のテンソル 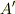 へ変換されている関係も分かると思います.上の例では,反変ベクトル
へ変換されている関係も分かると思います.上の例では,反変ベクトル 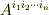 が共変ベクトル
が共変ベクトル 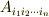 に移されるような例を挙げましたが,
に移されるような例を挙げましたが, 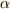 の添字の上下に応じて他ににも次のような組み合わせが考えられるでしょう.
の添字の上下に応じて他ににも次のような組み合わせが考えられるでしょう.
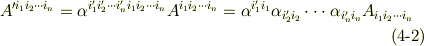
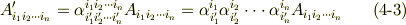
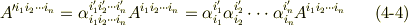
ポイントは,右辺で上下に分かれた二回現われている添字が消えているということです.
Important
直交変換に対し,変換則  〜
〜  のいずれかを満たす量
のいずれかを満たす量 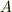 を
を  階テンソルと定義します.
階テンソルと定義します.
| [*] | 式  で二階や四階のテンソル, で二階や四階のテンソル,  や や 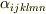 を二階のテンソルの積で書き換えましたが,このように書いて良い理由は次の 高階のテンソル で説明します. を二階のテンソルの積で書き換えましたが,このように書いて良い理由は次の 高階のテンソル で説明します. |
今の議論で,共変・反変の区別はあまり重要ではないので,以下のセクションでは特に断らない限り,ベクトルやテンソルは反変成分(例えば 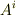 や
や 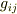 )で表わします.
)で表わします.
テンソルの成分
このセクションではテンソルの成分を考えてみます. 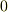 階のテンソルであるスカラーの成分は言うまでもなく
階のテンソルであるスカラーの成分は言うまでもなく 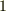 個です.次に,
個です.次に, 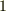 階のテンソルであるベクトル
階のテンソルであるベクトル 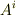 の成分は,
の成分は, 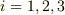 ですから
ですから 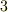 個です.二階のテンソル
個です.二階のテンソル 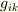 は,
は, 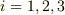 ,
, 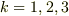 ですから,
ですから, 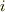 と
と 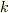 の組み合わせには
の組み合わせには  あって,
あって, 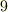 成分になります.階数に応じて成分数が
成分になります.階数に応じて成分数が  となっていますね.一般に
となっていますね.一般に  次のテンソルの成分は
次のテンソルの成分は 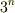 個になります.
個になります.
| [†] |  階テンソルの成分数が 階テンソルの成分数が 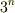 になるのは,座標系は三次元ユークリッド空間上に定義されると考えているからです.もし四次元ユークリッド空間ならば になるのは,座標系は三次元ユークリッド空間上に定義されると考えているからです.もし四次元ユークリッド空間ならば 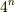 になりますし,一般に になりますし,一般に 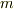 次元ユークリッド空間上の 次元ユークリッド空間上の  階テンソルは 階テンソルは  個の成分を持ちます.相対性理論で使うミンコフスキー空間は四次元ですので,相対論に出てくる 個の成分を持ちます.相対性理論で使うミンコフスキー空間は四次元ですので,相対論に出てくる  階テンソルの成分は 階テンソルの成分は 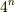 個になります.いつも三次元ユークリッド空間上で議論しているだけでいいのか,という点は 多様体の概念 で考察します. 個になります.いつも三次元ユークリッド空間上で議論しているだけでいいのか,という点は 多様体の概念 で考察します. |
| [‡] | テンソルを行列の一種だと思い込んでいる人に出くわすことがありますが,これは大変な誤解です.この原因は恐らく,物理や工学に出てくるテンソルの多くが二階のテンソルであり,二階のテンソルは  の行列の形に表現できることにあります.教科書によっては,テンソルの例として行列ばかりが出てくることも原因かも知れません.『テンソル=行列』ではありません!!式 の行列の形に表現できることにあります.教科書によっては,テンソルの例として行列ばかりが出てくることも原因かも知れません.『テンソル=行列』ではありません!!式 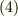 の変換則に従う量は全てテンソルと呼んでよく,その表現が行列である必要はありません.しかし, の変換則に従う量は全てテンソルと呼んでよく,その表現が行列である必要はありません.しかし,  の行列は常に二階のテンソルになることを示せます.つまり,テンソルの表現は必ずしも行列には限らないけれども, の行列は常に二階のテンソルになることを示せます.つまり,テンソルの表現は必ずしも行列には限らないけれども,  行列と三次元ベクトルの演算は二階のテンソルの変換則を必ず満たすということです.このような事情で,あたかもテンソルは全て行列であるかのように誤解を招く書き方をする教科書さえあるのだと思われます.注意してください. 行列と三次元ベクトルの演算は二階のテンソルの変換則を必ず満たすということです.このような事情で,あたかもテンソルは全て行列であるかのように誤解を招く書き方をする教科書さえあるのだと思われます.注意してください. |
基底を使った定義
前のセクションでは,テンソルを座標変換の際の変換則によって定義しました.式  の変換則は今後も頻繁に使うものですから,しっかり覚えておいて下さい.しかし,変換則だけでは添字をこちょこちょいじっているだけのようで,どうも定義としてパンチに欠けます. もう一度だけ内積外積 で既に紹介した定義ですが,ベクトルの延長としてテンソルを定義した方が直観的に納得しやすいかも知れません..
の変換則は今後も頻繁に使うものですから,しっかり覚えておいて下さい.しかし,変換則だけでは添字をこちょこちょいじっているだけのようで,どうも定義としてパンチに欠けます. もう一度だけ内積外積 で既に紹介した定義ですが,ベクトルの延長としてテンソルを定義した方が直観的に納得しやすいかも知れません..
ベクトル  は適当な基底
は適当な基底  を使って次のように表現できました.
を使って次のように表現できました.
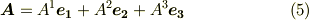
もしくは,その成分を括弧でくくって  のように書けました. ベクトルは一階のテンソルであることを再確認して下さい.
のように書けました. ベクトルは一階のテンソルであることを再確認して下さい.
次に,ベクトルの基底  を二つ組み合わせて作った基底
を二つ組み合わせて作った基底 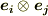 を考えると,このような基底には
を考えると,このような基底には  で
で 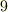 種類があり,その成分
種類があり,その成分 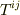 として二階のテンソルを表現することができます.
として二階のテンソルを表現することができます.
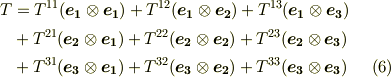
新しく作った基底 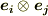 って何なんだYO!という疑問はまぁ置いておいて,表現の仕方としては,式
って何なんだYO!という疑問はまぁ置いておいて,表現の仕方としては,式  をそのまま二次に拡張したのが式
をそのまま二次に拡張したのが式 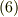 になっているという点は,見て納得できると思います.成分だけを次のように書いても良いでしょう.
になっているという点は,見て納得できると思います.成分だけを次のように書いても良いでしょう.  の行列の形にまとめて書くのが便利です.これも,ベクトル成分を括弧で書いたことの拡張です.
の行列の形にまとめて書くのが便利です.これも,ベクトル成分を括弧で書いたことの拡張です.
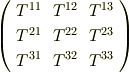
さらに,ベクトルの基底  を三つ組み合わせれば三階のテンソルになります.三階のテンソルの基底は
を三つ組み合わせれば三階のテンソルになります.三階のテンソルの基底は 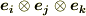 の形で,成分は
の形で,成分は  のようになります.(
のようになります.( 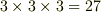 成分ですね.)さらに一般には,ベクトルの基底
成分ですね.)さらに一般には,ベクトルの基底  を
を  個組み合わせた基底
個組み合わせた基底  と,その成分
と,その成分 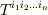 を使ってテンソルは次のように書けます.(右辺は縮約により,和になっています.)
を使ってテンソルは次のように書けます.(右辺は縮約により,和になっています.)
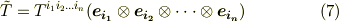
こう見てくると,ベクトルは確かにテンソルの特殊な場合だということが分かると思います.基底を使ったテンソルの定義  と,座標系を直交変換する際の変換則を使ったテンソルの定義式
と,座標系を直交変換する際の変換則を使ったテンソルの定義式 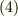 は,異なる定義のように思えますが,実は,式
は,異なる定義のように思えますが,実は,式  のようにベクトルを幾つか組み合わせてテンソルを作るとき,その成分
のようにベクトルを幾つか組み合わせてテンソルを作るとき,その成分  はちゃんと式
はちゃんと式 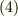 の座標変換の式を満たすことが示せます.逆に,任意の
の座標変換の式を満たすことが示せます.逆に,任意の  階テンソルは
階テンソルは  個のベクトルを組み合わせたものとして表現することが出来ます.ですから,座標変換の式による定義
個のベクトルを組み合わせたものとして表現することが出来ます.ですから,座標変換の式による定義 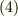 と,『ベクトルを組み合わせてテンソルを作る』という定義
と,『ベクトルを組み合わせてテンソルを作る』という定義  は数学的に同値なのです.どちらの視点も大事です. ベクトルからテンソルを作る でこの問題を少し掘り下げてみます.
は数学的に同値なのです.どちらの視点も大事です. ベクトルからテンソルを作る でこの問題を少し掘り下げてみます.
Important
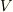 をベクトルとして,
をベクトルとして, 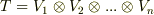 を
を  階テンソルと定義しても良いです.
階テンソルと定義しても良いです.
ただし,私達はまだ,この掛け算のような記号 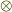 が何なのかきちんと考えていません.これを テンソル積 と呼びますが, 双線形関数 から テンソル代数 にかけて,テンソル積についてはよく考えてみたいと思います.テンソルの代数的構造を探るには,多少,線形代数や代数学の知識が必要になります.
が何なのかきちんと考えていません.これを テンソル積 と呼びますが, 双線形関数 から テンソル代数 にかけて,テンソル積についてはよく考えてみたいと思います.テンソルの代数的構造を探るには,多少,線形代数や代数学の知識が必要になります.
| [§] | テンソルの持つ性質で非常に大事なものに,もうひとつ多重線形性と呼ばれるものがあります.この多重線形性をテンソルの定義にしても良いのですが,少し難しいので後回しにします.多重線形性については 多重線形性とテンソル空間 で考えます. |
| [¶] | ベクトルの計算しかしていなかったときは,ベクトルとベクトルの積と言えば,内積か外積しかありませんでしたから,何となく 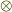 という積が気持ち悪いと思っている人がいるかも知れません.そもそも,ベクトルを勉強した時に内積と外積しか習わなかったのは,そのときにベクトルかスカラーしか知らなかったからです.一般に,積というのは一種の作用ですから,何か新しいものが生成されます.その生成物が今までに知っているものなら良いですが,知らないものなら,また新しく勉強しないといけません. という積が気持ち悪いと思っている人がいるかも知れません.そもそも,ベクトルを勉強した時に内積と外積しか習わなかったのは,そのときにベクトルかスカラーしか知らなかったからです.一般に,積というのは一種の作用ですから,何か新しいものが生成されます.その生成物が今までに知っているものなら良いですが,知らないものなら,また新しく勉強しないといけません.  は二階のテンソルという,ベクトルやスカラーとはまた違ったものになっている点に注意してください. は二階のテンソルという,ベクトルやスカラーとはまた違ったものになっている点に注意してください. |
物理学におけるテンソル
このように,テンソルとは多数の成分からなる,ベクトルのお化けのような量だということが分かりましたが,テンソルの添字が座標系を表わす番号であったことを思い出せば,多少とも物理的な例を考えてイメージを持つことが出来ると思います.
スカラー
零階のテンソルであるスカラーは,その表現も変換則も座標系によりません.ということは,もしもある物理量がスカラーならば,その値はどの座標系から観測しても変わらないはずです.
アインシュタインが相対性理論を考える発端となった疑問は,光速で飛んでいる人が光を観測したら,どのような速度に見えるだろうか,いう問題でした.結論から言えば,光速はどこから観測しても一定に見えるそうですが,それは光速がスカラーだからです.
| [#] | ベクトルの内積はスカラーですから座標不変量で,座標系には寄らないはずです.内積を双対ベクトルを使って 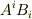 のように添字が上下に分かれるように書くと,座標系と関係ない形になるのでしたが,実はより高次のテンソルの積を取る場合も,添字が上下に分かれているものは座標不変量になります.これをテンソルの内積と呼び,テンソルの演算で非常に重要な性質です. のように添字が上下に分かれるように書くと,座標系と関係ない形になるのでしたが,実はより高次のテンソルの積を取る場合も,添字が上下に分かれているものは座標不変量になります.これをテンソルの内積と呼び,テンソルの演算で非常に重要な性質です. |
| [♠] | ただし,相対論で考える座標系は,空間の三次元に時間を足したミンコフスキー空間と呼ぶ四次元の座標系で,座標変換の式をローレンツ変換と呼びます.ミンコフスキーだとかローレンツだとか四次元だとか,なんだか難しそうに思うかも知れませんが,要するに座標変換の話に過ぎません. |
ベクトル
一階のテンソルであるベクトルは,  のように
のように 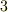 つの成分だけからなります.これは座標よって見え方の変わる量で,古典力学の範囲では,力,速度,位置,加速度,物体の回転モーメントなどが代表例です.
つの成分だけからなります.これは座標よって見え方の変わる量で,古典力学の範囲では,力,速度,位置,加速度,物体の回転モーメントなどが代表例です.
| [♥] | ベクトルもテンソルですから,座標変換の式 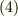 を満たします.その意味で,ベクトルは単にスカラーを3つひとまとめにしたものとは違います.例えば,理想気体の状態は体積 を満たします.その意味で,ベクトルは単にスカラーを3つひとまとめにしたものとは違います.例えば,理想気体の状態は体積 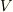 ,密度 ,密度 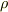 ,温度 ,温度 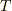 という,三つのスカラーの組として表現されますが, という,三つのスカラーの組として表現されますが, 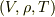 はベクトルではありません. はベクトルではありません. 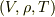 は式 は式 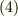 を満たさないからです.『成分が座標系による』という性質が本質的に重要です.ベクトルを,単に を満たさないからです.『成分が座標系による』という性質が本質的に重要です.ベクトルを,単に 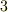 つのスカラーを括弧でひとまとめにしたものだと思っていた人は,もう一度,一階のテンソルという視点でベクトルを考え直してみてください.また,ベクトルを『向きと大きさのある量』だと思っていた人も,このイメージでは不十分です.例えば,非等方性結晶の弾性定数や屈折率などはベクトルではありませんが,大きさと向きを持った量になります.こうした紛らわしい量が出てきたら,式 つのスカラーを括弧でひとまとめにしたものだと思っていた人は,もう一度,一階のテンソルという視点でベクトルを考え直してみてください.また,ベクトルを『向きと大きさのある量』だと思っていた人も,このイメージでは不十分です.例えば,非等方性結晶の弾性定数や屈折率などはベクトルではありませんが,大きさと向きを持った量になります.こうした紛らわしい量が出てきたら,式 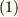 を満たすかどうかをチェックして下さい.式 を満たすかどうかをチェックして下さい.式 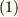 を満たす量はベクトル,満たさない量はベクトルではない,と定義すればすっきりします. を満たす量はベクトル,満たさない量はベクトルではない,と定義すればすっきりします. |
二階のテンソル
ベクトル  を,
を, 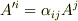 のように変換する量
のように変換する量 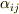 は二階のテンソルです.この式を『
は二階のテンソルです.この式を『 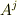 を変数とする関数
を変数とする関数 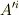 』と考えて,物理的状況を考えてみましょう.
』と考えて,物理的状況を考えてみましょう.
いま第一成分 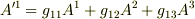 を考えると,
を考えると, 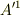 の変化が
の変化が 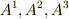 の全ての変化に関係するという意味だと解釈できます.この状況の例として,弾性のある物体に力をかけた場合の変位を挙げられます.消しゴムのようなものをギュウと押すと,力を加えた方向に縮むだけでなく,横にも広がりますね.(もしくはゴムを引っ張ると,引っ張った方向に伸びるだけでなく,太さは細くなります.)縦の変化と横の変化が相関している訳ですが,このような状況を表わすのが二階のテンソルです.この例は材料力学に出てくる,応力-ひずみテンソルというものです.( 材料力学 を参照してください.)
の全ての変化に関係するという意味だと解釈できます.この状況の例として,弾性のある物体に力をかけた場合の変位を挙げられます.消しゴムのようなものをギュウと押すと,力を加えた方向に縮むだけでなく,横にも広がりますね.(もしくはゴムを引っ張ると,引っ張った方向に伸びるだけでなく,太さは細くなります.)縦の変化と横の変化が相関している訳ですが,このような状況を表わすのが二階のテンソルです.この例は材料力学に出てくる,応力-ひずみテンソルというものです.( 材料力学 を参照してください.)
力学に出てくる二階のテンソルの例としては,慣性モーメントも重要です.慣性モーメントは,物体の縦・横のやせ具合(太り具合)と,縦・横の軸の周りの回しやすいさの関係を示す量ですので,やはり二階のテンソルで上手く表現されます.一般に縦の変化と横の変化が相関する物理現象には二階のテンソルがよく顔を出します.力学や材料力学の教科書が手元にあれば,これらの例の物理的意味をもう一度復習してみて下さい.
すでにお馴染みのクロネッカーのデルタも実は二階のテンソルです(添字が二つですね).クロネッカーのデルタの行列表記は次のようになります.
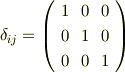
| [♦] | 三階以上のテンソルの物理的かつ直観的イメージはどのように表現できるでしょうか?読者のみなさんに,何か分かりやすいイメージを持っている方がいたら,ぜひ教えてください. |