定数係数1階線形微分方程式
微分方程式というのは,その名の通り方程式に微分が入っている,
つまり導関数が入っている方程式のことです.
いろいろな形( 変数分離形 など)があるのですが,ここではつぎのようなものを学びます.
 を定数,
を定数, 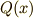 をある連続な関数とするとき,
をある連続な関数とするとき,
 の関数である未知関数
の関数である未知関数 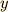 と,その導関数
と,その導関数 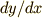 に関して1次式である,
に関して1次式である,

のうな形で表される微分方程式です. これを,定数係数1階線形微分方程式といいます. この形の微分方程式について,これからお話します (え,なぜかって?そりゃあ,よく使うからですよ♪).
定数係数1階線形微分方程式の解の公式
いきなりですが,いま考えている微分方程式の解の公式を示します.式 (1)
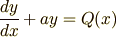
の一般解は

で与えられます.ここで  は任意定数です.
は任意定数です.
未知関数 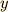 についての微分方程式を「解く」とは,
おおざっぱに言うと
についての微分方程式を「解く」とは,
おおざっぱに言うと 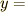 の形に持って行く,ということです.
ですから,式 (1) が式 (2) に変形できることが分かっていれば,
これはもう,いつでも解けるわけです.
といっても,こんな公式を丸暗記していたら大変です.
手順を理解し,いつでも導出できるようにすることが重要です.
の形に持って行く,ということです.
ですから,式 (1) が式 (2) に変形できることが分かっていれば,
これはもう,いつでも解けるわけです.
といっても,こんな公式を丸暗記していたら大変です.
手順を理解し,いつでも導出できるようにすることが重要です.
導出
ではここで,式 (2) を導出してみます. まず,積分を簡単にするために式 (1) の左辺
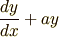
を

のような,「ある一つの関数  の微分」の形に変形することを考えます.
そのために,式 (1) の両辺に
の微分」の形に変形することを考えます.
そのために,式 (1) の両辺に 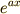 をかけますと
をかけますと
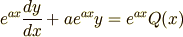
となります.ここで, 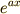 の微分が
の微分が 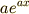 となる性質を思い出します.
すなわち上式は
となる性質を思い出します.
すなわち上式は
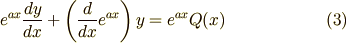
と変形できることになります.ここまで,よろしいでしょうか.
さらにもう一つ,積の微分公式
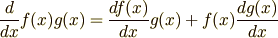
を式 (3) の左辺に適用します.すると
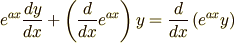
がいえます.これは最初目指していた形です.ですから結局,式 (3) は
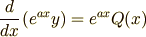
という形になるのです.ここまでくれば簡単,あとは両辺を  で積分して
で積分して

が得られます.ここで  は任意定数です.
左辺を「ある一つの関数
は任意定数です.
左辺を「ある一つの関数  の微分」という形に
変形したかった理由は,このように両辺を一気に積分したかったからです.
この方法は一般的に良く使うテクニックですので,憶えていておいて損はないでしょう.
の微分」という形に
変形したかった理由は,このように両辺を一気に積分したかったからです.
この方法は一般的に良く使うテクニックですので,憶えていておいて損はないでしょう.
最後に,式 (4) の両辺に 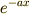 をかけますと,
をかけますと,

という,最初に示した式 (2) が得られるのです.
例題
それでは,簡単な例題を示しておきます.
例題1
つぎの定数係数1階線形微分方程式(長い名前だ…)
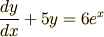
の一般解を求めます.まず,さきほどの導出の手順にしたがって,
両辺に 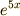 をかけます.すると
をかけます.すると
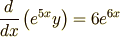
となります(ここで一気に積の微分公式による変形も行っています).
上式の両辺を  で積分して
で積分して
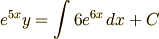
となり(  は任意定数),さらに両辺に
は任意定数),さらに両辺に  をかけると
をかけると

という一般解を得ます.
例題2
速さ  に比例する抵抗が働くとき,質点の鉛直方向の運動方程式は
に比例する抵抗が働くとき,質点の鉛直方向の運動方程式は
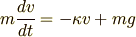
と表せます.ここで 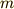 を質点の質量,
を質点の質量, 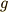 を重力加速度としています.
この運動方程式は 変数分離形 として解くこともできますが,
定数係数1階線形微分方程式であるとも言えますので,これまでの方法で解いてみます.
を重力加速度としています.
この運動方程式は 変数分離形 として解くこともできますが,
定数係数1階線形微分方程式であるとも言えますので,これまでの方法で解いてみます.
式を少し変形して

両辺に  をかけ,積の微分公式から整理すると
をかけ,積の微分公式から整理すると
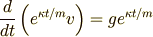
両辺を 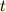 で積分して
で積分して
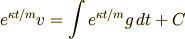
を得,両辺に 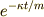 をかけると
をかけると
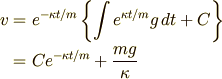
という速度の一般解を得ます.ここで  は任意定数です.
ちなみにこういった任意定数は,初期条件に依って決まります.
この例題について詳しくは, 抵抗力のある落下運動 をご覧ください.
は任意定数です.
ちなみにこういった任意定数は,初期条件に依って決まります.
この例題について詳しくは, 抵抗力のある落下運動 をご覧ください.
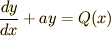 において
において 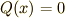 の場合,すなわち
の場合,すなわち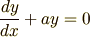
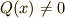 の場合は非同次方程式と呼ばれます.
同次方程式の一般解
の場合は非同次方程式と呼ばれます.
同次方程式の一般解 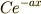 (
( 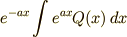 (
(