変数分離形
微分方程式が

という形のとき,変数分離形と呼びます.微分方程式のなかで一番基本となる形です.
変数分離形の解法
これを解くにはまず,左辺,右辺を同じ変数だけにまとめます.つまり変数を分離するんです.
変数の分離
式 (1) の場合では左辺を変数が 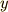 のものに,右辺を変数が
のものに,右辺を変数が  のもにまとめます.
のもにまとめます.
両辺に 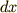 を掛けると
を掛けると

となり,さらに両辺を 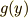 で割ってやる(
で割ってやる( 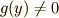 とする)と
とする)と
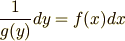
となります.イコールをはさんで左右に変数が分離できました.
両辺を積分
つぎに両辺を積分します.
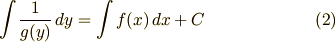
ここで  は任意定数(積分定数)です.このあと式 (2) の積分を計算し,
は任意定数(積分定数)です.このあと式 (2) の積分を計算し,
 の形にしてやれば「微分方程式が解けた」ということになります.
任意定数を含む式 (2) は一般解と呼ばれ,
の形にしてやれば「微分方程式が解けた」ということになります.
任意定数を含む式 (2) は一般解と呼ばれ,
 は初期条件や境界条件から決まります
(初期条件などが分からない場合はそのまま放っておきます).
は初期条件や境界条件から決まります
(初期条件などが分からない場合はそのまま放っておきます).
例題
では具体例を解いてみましょう.解くのは
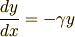
という微分方程式です.まずは変数の分離です.
左辺に 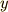 を,右辺に
を,右辺に  をまとめましょう.
両辺に
をまとめましょう.
両辺に 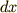 を掛けると
を掛けると

で,さらに両辺を 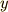 で割ると
で割ると

となって変数分離が完了です.つぎに両辺を積分します.

ここで
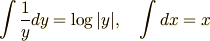
ですから,式 (3) は
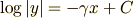
となります.両辺の指数をとると(→ “指数をとる”につて 参照)
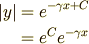
したがって
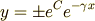
となります.  が定数なので
が定数なので 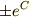 も定数ですから,
これを新しく
も定数ですから,
これを新しく 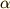 という記号で置き換えると
という記号で置き換えると

となります. 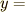 の形になったので,これで変数分離形の常微分方程式が解けました.
の形になったので,これで変数分離形の常微分方程式が解けました.
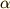 は初期条件から決まる定数です.
は初期条件から決まる定数です.
初期条件を仮定してみる
ついでなので, 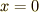 のとき
のとき 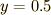 という初期条件を
仮定して
という初期条件を
仮定して 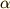 を求めてみます.初期条件を微分方程式の解に代入すると
を求めてみます.初期条件を微分方程式の解に代入すると

で 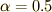 と求まりました.したがって仮定した初期条件のもとでの解は
と求まりました.したがって仮定した初期条件のもとでの解は
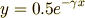
である,ということになります.
このように変数分離形の微分方程式は決まった手続きで解くことができます. ほかにもいろいろな形の微分方程式がありますが, 多くの場合,式を変形して最終的に変数分離形にもっていって解くことになります. もう少し例を上げると

なども変数分離形です.暇があればぜひ解いてみてください.