抵抗力のある落下運動

初歩の物理の問題では抵抗を無視することが多いですが，現実にはもちろん抵抗力は無視できない大きさで存在します．もしも空気の抵抗がなかったら上から落ちる物はどんどん加速するので，僕たちは雨の日には外を出歩けなくなってしまいます．雨に当たって死んじゃう．

空気や液体の抵抗力はいろいろと複雑なのですが，一番簡単なのは速度に比例した力を受けるものです．自転車なんかでも，速く漕ぐほど受ける風は大きくなり，速度を大きくするのが難しくなります．空気抵抗から受ける力の向きは，もちろん進行方向に逆向きです．

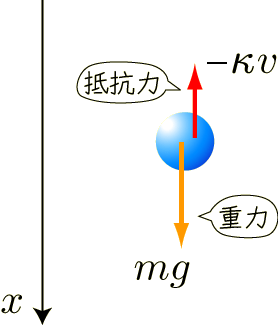
質量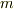のなにかが落下する運動を考えて，図のように座標軸をとり，運動方程式で記述してみましょう．そして運動方程式を解いて，抵抗を受ける場合の速度と位置の変化がどうなるかを調べてみます．

運動方程式

落ちる物体の質量を 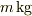$m \unit{kg}$ ，重力加速度を 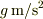$g \unit{m/s^2}$ ，空気抵抗の比例係数を $\kappa$ （カッパ）とします．物体に働く力は軸の正方向に重力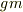，負方向に空気抵抗 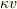$\kappa v$ だけですから，運動方程式は

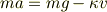
$ma = mg - \kappa v$

となります．加速度を速度の微分形の形で書くと

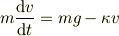
$m\frac{\mathrm{d}v}{\mathrm{d}t} = mg-\kappa v$

というものになります．これは 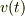v(t) に関する1階微分方程式です．

速度の式を求める

積分して 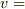v = の形にしたいので変数を分離します．両辺を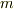で割って

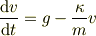
$\frac{\mathrm{d}v}{\mathrm{d}t} = g - \frac{\kappa}{m}v$

ここで右辺をの係数で括ります．

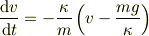
$\frac{\mathrm{d}v}{\mathrm{d}t} = -\frac{\kappa}{m}\left(v-\frac{mg}{\kappa}\right)$

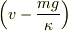両辺を $\displaystyle \left(v-\frac{mg}{\kappa}\right)$ で割ります．

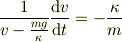
$\frac{1}{v-\frac{mg}{\kappa}}\frac{\mathrm{d}v}{\mathrm{d}t} = -\frac{\kappa}{m}$

両辺に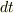を掛けます．

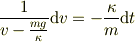
$\frac{1}{v-\frac{mg}{\kappa}}\mathrm{d}v = -\frac{\kappa}{m}\mathrm{d}t$

これで変数が分離された形になりました．両辺を積分します．

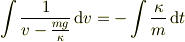
$\int\frac{1}{v-\frac{mg}{\kappa}}\,\mathrm{d}v = -\int\frac{\kappa}{m}\,\mathrm{d}t$

積分公式 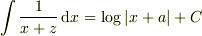$\int\frac{1}{x+z}\,\mathrm{d}x=\log\vert x+a\vert+C$ より

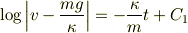
$\log\left\vert v-\frac{mg}{\kappa}\right\vert = -\frac{\kappa}{m}t+C_1$

両辺の指数をとると（ “指数をとる”について参照）

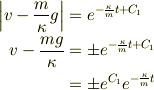
$\left\vert v-\frac{m}{\kappa}g\right\vert &= e^{-\frac{\kappa}{m}t+C_1}\\v-\frac{mg}{\kappa} &= \pm e^{-\frac{\kappa}{m}t+C_1}\\ &= \pm e^{C_1}e^{-\frac{\kappa}{m}t}$

ここで 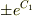$\pm e^{C_1}$ を新たに任意定数 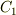C_1 とおくと，

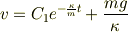
$v = C_1e^{-\frac{\kappa}{m}t}+\frac{mg}{\kappa}$

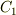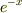となり，速度の式が分かりました．任意定数 C_1 は初期条件によって決まる値です．この速度の式，斜面を滑べる運動とはちょっと違います．時間がの肩に付いているところが違います．しかもの肩はマイナスの係数です． $e^{-x}$ のグラフは

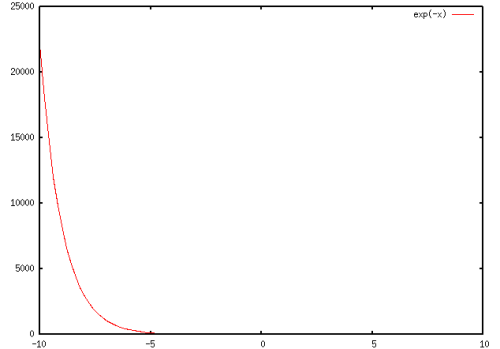
のようになるので，最終的に時間に関する項はゼロになり，速度は 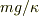$mg/\kappa$ という一定値になることが分かります．この速度を終端速度といいます．雨粒がものすごく速いスピードにならないことが，運動方程式から理解できたことになります．よかったですね（誰に言ってんだろ）．

位置の式を求める

速度の式が分かったので，つぎは位置について求めます．速度を位置の微分の形で書くと

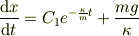
$\frac{\mathrm{d}x}{\mathrm{d}t} = C_1e^{-\frac{\kappa}{m}t}+\frac{mg}{\kappa}$

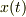関数 x(t) の1階微分方程式になります．これを解いて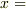の形にしてやります．変数を分離して

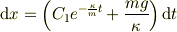
$\mathrm{d}x = \left(C_1e^{-\frac{\kappa}{m}t}+\frac{mg}{\kappa}\right)\mathrm{d}t$

この両辺を積分します．

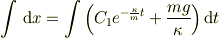
$\int\,\mathrm{d}x = \int\left(C_1e^{-\frac{\kappa}{m}t}+\frac{mg}{\kappa}\right)\mathrm{d}t$

積分公式 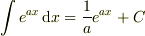$\int e^{ax}\,\mathrm{d}x=\frac{1}{a}e^{ax}+C$ より

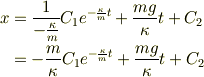
$x &= \frac{1}{-\frac{\kappa}{m}}C_1e^{-\frac{\kappa}{m}t}+\frac{mg}{\kappa}t+C_2\\ &= -\frac{m}{\kappa}C_1e^{-\frac{\kappa}{m}t}+\frac{mg}{\kappa}t+C_2$

という位置の式が求まりました．任意定数 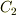C_2 も初期条件から決まります．速度の式でみたように，十分時間が経つと速度は一定になるので，位置の式も時間が経つと等速度運動で表されることになります．

[home] [力学] [ページの先頭]