分離拡大体
すでに 既約と可約 で,次の定理を見ました.ただし,註にも書いたことですが,この定理がなりたつのは体の標数が 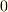 のときだけだという点に注意してください.
のときだけだという点に注意してください.
theorem
標数 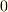 の体上で既約な方程式
の体上で既約な方程式 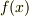 は,重解を持ちません.
は,重解を持ちません.
証明は既に与えてありますが,標数が零ではない体の場合も考えてみるために,まず次節で, 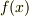 の導関数
の導関数 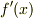 を使って方程式の重解の有無を判別する方法を導入します.
を使って方程式の重解の有無を判別する方法を導入します.
標数0の場合
体 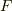 上の多項式
上の多項式 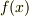 が
が 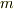 重解
重解 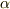 を持ち,
を持ち, 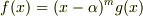 と書けるとすると,その微分は
と書けるとすると,その微分は 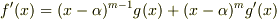 となり,やはり
となり,やはり  を因数に持ちます.よって,この場合
を因数に持ちます.よって,この場合 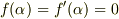 が成り立ちます.
が成り立ちます. 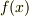 と
と 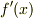 はどちらも
はどちらも  上の多項式ですが,公約元
上の多項式ですが,公約元  を持ちますので,既約ではありません.
を持ちますので,既約ではありません.
一方, 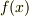 が 重解を持たないならば,
が 重解を持たないならば, 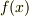 と
と 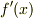 は公約元を持たず,
は公約元を持たず, 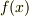 の解
の解 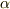 に対しても,一般には
に対しても,一般には  となります.
となります.
標数≠0の場合
標数 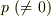 の体
の体 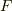 を考えます.つまり,
を考えます.つまり, 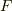 の元
の元  は全て
は全て 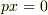 を満たすということです.この体
を満たすということです.この体 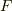 上で,方程式
上で,方程式 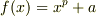 を考えて見ましょう.これは確かに既約ですが,標数が
を考えて見ましょう.これは確かに既約ですが,標数が 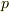 であることより,その導関数は
であることより,その導関数は 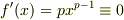 となってしまいます.つまり,既約であっても,標数が零でなければ,導関数が零となる場合があるということです.
となってしまいます.つまり,既約であっても,標数が零でなければ,導関数が零となる場合があるということです.
導関数が 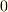 の場合,既約な方程式が重解を持つ可能性のあることは, 標数 の記事で式
の場合,既約な方程式が重解を持つ可能性のあることは, 標数 の記事で式 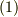 として導いた次の公式からも分かります.
として導いた次の公式からも分かります.
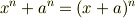
左辺は既約ですが,右辺は 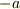 が
が  重根であることを示しています.標数が
重根であることを示しています.標数が 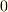 でない体の場合は要注意です!!
でない体の場合は要注意です!!
まとめ
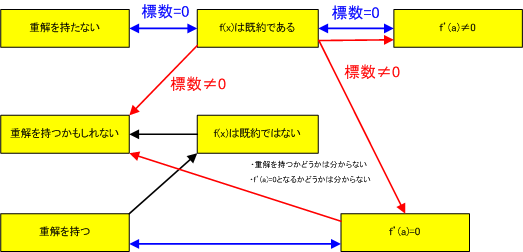
ここまで出てきた事柄を整理します.全部書くとややこしいので,フローチャート式の図にしてみました.  の解を
の解を  としています.標数の場合分けと論理関係に注意してください.
としています.標数の場合分けと論理関係に注意してください.
既約な多項式 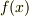 で,その解
で,その解  に対して
に対して 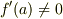 となるものを 分離多項式 と呼びます.分離多項式は重解を持ちません.逆に,既約であっても
となるものを 分離多項式 と呼びます.分離多項式は重解を持ちません.逆に,既約であっても 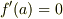 となるものを 非分離多項式 と呼びます.図中,標数
となるものを 非分離多項式 と呼びます.図中,標数 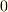 の場合を青い矢印で,標数
の場合を青い矢印で,標数 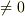 の場合を赤い矢印で示しました.標数に関わりなく成り立つ関係は,黒い矢印で示しました.上の段の, 青い矢印で結ばれた三つの条件は,どれも分離多項式の条件として同値なもの です.また,標数が零でない体上では,既約であっても
の場合を赤い矢印で示しました.標数に関わりなく成り立つ関係は,黒い矢印で示しました.上の段の, 青い矢印で結ばれた三つの条件は,どれも分離多項式の条件として同値なもの です.また,標数が零でない体上では,既約であっても 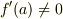 が言えません. 既約な多項式が非分離となるのは体の標数が非零の場合だけ です.
が言えません. 既約な多項式が非分離となるのは体の標数が非零の場合だけ です.
Important
標数 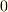 ならば,既約な多項式は全て分離多項式です.
ならば,既約な多項式は全て分離多項式です.
分離拡大体は重解を持たないのですから,適当な分解拡大体上で,一次式の積にバラバラに因数分解できるはずです.分離拡大体は,重解を持たない既約方程式の 解を添加して得られる拡大体だ とも言えます.

| [*] | 既約な方程式の話に微分が出てきましたが,これは単に多重解に対応する因数分解の部分 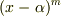 の次数を一個下げるために顔を出してきた道具であって,ここで急に解析学が関係してくるわけではありません.分離多項式の心とは『重解を持たない既約多項式である』ということです. の次数を一個下げるために顔を出してきた道具であって,ここで急に解析学が関係してくるわけではありません.分離多項式の心とは『重解を持たない既約多項式である』ということです. |
| [†] | 最小多項式だとか,方程式が因数分解できるかとか,そのような話題で急に拡大体を分類し始めたのには,この後,方程式論に体論を利用してやろうという狙いがあるからです.いま抽象的な概念がしっくり来ない人も,ガロア理論の章で五次方程式に解の公式が無いことを示す予定ですから,そのような具体例を勉強したあとで復習すると用語の意味がはっきりするかも知れません. |
分離的・非分離的
体 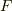 の代数的な元
の代数的な元  を考えましょう.代数的であるとは,
を考えましょう.代数的であるとは,  を解とする代数方程式が
を解とする代数方程式が 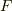 上にあるということです.いま,
上にあるということです.いま, 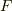 上の
上の  の最小多項式
の最小多項式 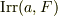 が分離多項式であるとき, aはF上分離的である といいます.最小多項式が非分離的ならば,
が分離多項式であるとき, aはF上分離的である といいます.最小多項式が非分離的ならば,  は
は 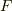 上非分離的である,と言います.
上非分離的である,と言います.
最小多項式が分離的か非分離的かで,元が分離的か非分離的かを定義するわけです.
分離拡大体
体 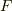 の拡大体
の拡大体 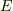 において,
において, 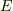 の元が全て
の元が全て 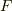 上分離的であるとき,
上分離的であるとき, 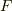 を
を 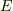 の 分離拡大体 と言います.
の 分離拡大体 と言います. 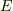 の元は全て,
の元は全て, 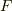 上の分離多項式の解として表わされるということです.逆に,
上の分離多項式の解として表わされるということです.逆に, 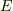 上にひとつでも
上にひとつでも 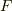 上非分離的な元が入っていれば,
上非分離的な元が入っていれば, 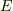 は
は 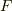 の 非分離拡大体 であると言います.
の 非分離拡大体 であると言います.
分離拡大は,代数的拡大の特別な場合と言えます( 代数的拡大体 参照).ですから, 全ての分離拡大体は代数的拡大体です が,その逆は言えません.代数的拡大体であっても,体の標数が非零ならば非分離的なものがあります.
ある体の代数的拡大体が全て分離拡大体になる場合,この体を 完全体 と呼びます.有理数体,実数体などは完全体です.このあと,ガロア理論の章では標数 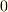 の体ばかりを考えますから,基本的に非分離拡大体など出てきません.のちほど勉強する ガロア拡大体 も,分離拡大体の一種です.
の体ばかりを考えますから,基本的に非分離拡大体など出てきません.のちほど勉強する ガロア拡大体 も,分離拡大体の一種です.
| [‡] | この後の議論では,有理数体 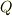 の代数的拡大体ばかり考えますので,そこに出てくる代数的拡大体は全て分離的です.標数が の代数的拡大体ばかり考えますので,そこに出てくる代数的拡大体は全て分離的です.標数が 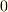 ではない体上の方程式を考えることは滅多にありませんので,実際問題,あまり非分離という事態を気にすることはありません.しかしせっかくですので,言葉の定義と概念は正確に覚えておきましょう. ではない体上の方程式を考えることは滅多にありませんので,実際問題,あまり非分離という事態を気にすることはありません.しかしせっかくですので,言葉の定義と概念は正確に覚えておきましょう. |
分離閉包
体 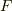 上の代数方程式の解を全て含む
上の代数方程式の解を全て含む 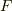 の拡大体
の拡大体 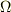 を代数的閉包と呼ぶことは,既に 最小分解体と代数的閉体 で見ました.
を代数的閉包と呼ぶことは,既に 最小分解体と代数的閉体 で見ました. 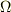 の元のうち,
の元のうち, 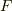 上分離的な元だけによる集合を 分離閉包 と呼びます.
上分離的な元だけによる集合を 分離閉包 と呼びます.
ここでは証明は省略しますが,分離閉包も体になります