最小分解体・代数的閉体
体 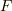 上,既約な
上,既約な  次多項式
次多項式 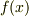 を考えます.
を考えます.
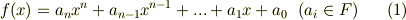
既約ですから 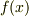 は
は 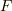 上ではこれ以上因数分解できませんが,
上ではこれ以上因数分解できませんが, 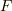 の拡大体
の拡大体 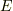 上では,一次関数の積の形に因数分解可能かも知れません.複素数体にまで拡大すれば必ず因数分解可能であることが 代数学の基本定理 によって保証されているのですから,この予想は的外れではないでしょう.
上では,一次関数の積の形に因数分解可能かも知れません.複素数体にまで拡大すれば必ず因数分解可能であることが 代数学の基本定理 によって保証されているのですから,この予想は的外れではないでしょう.
拡大体 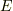 上で,多項式が一次関数の積の形に因数分解可能な場合,そのような
上で,多項式が一次関数の積の形に因数分解可能な場合,そのような 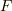 の拡大体
の拡大体 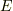 を『
を『 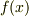 の
の 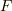 上の 分解体 』と呼びます.
上の 分解体 』と呼びます. 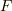 と複素数体の間には,一般に無限に分解体がありますが,特に分解体で最小のものを 最小分解体 と呼びます.『
と複素数体の間には,一般に無限に分解体がありますが,特に分解体で最小のものを 最小分解体 と呼びます.『 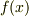 をバラバラに因数分解可能できる最小の拡大体』という意味です.多項式の解がどの体上にあるかは個々の多項式によって異なりますから,最小分解体は, 個々の方程式に対して一つずつ決まる ものです
をバラバラに因数分解可能できる最小の拡大体』という意味です.多項式の解がどの体上にあるかは個々の多項式によって異なりますから,最小分解体は, 個々の方程式に対して一つずつ決まる ものです
方程式の解でもとの体に含まれないものを,必要最小限だけ添加して得られる拡大体が最小分解体だと考えることもできます.
有理数体 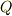 上の方程式に対して,最小分解体は必ず存在し,一意的に決まることが知られています.ここでは証明は省略します. 代数学の基本定理 によって少なくとも複素数体は
上の方程式に対して,最小分解体は必ず存在し,一意的に決まることが知られています.ここでは証明は省略します. 代数学の基本定理 によって少なくとも複素数体は 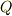 上のどんな方程式に対しても分解体になるわけですから,最小分解体の存在は明らかでしょう.
上のどんな方程式に対しても分解体になるわけですから,最小分解体の存在は明らかでしょう.
代数的閉体,代数的閉包
体 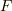 の全ての代数方程式
の全ての代数方程式 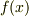 が
が 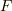 上に解を持つとき,
上に解を持つとき, 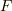 を 代数的閉体 と呼びます.
を 代数的閉体 と呼びます.
有理係数の方程式が無理数の解を持ったり,実係数の方程式の解が複素数になったりしますから,有理数体や実数体は代数的閉体ではありません.しかし,複素数体上の方程式は解を全て複素数体上に持ちますから, 複素数体は代数的閉体です . 代数学の基本定理 は,複素数体が代数的閉体であることを主張していると読み換えることも出来ます.
次の三つの条件は,代数的閉体の定義として,どれも同値なものです.つまり代数的閉体は『これ以上体の拡大をしなくても,方程式を解くのに一人で困らない体』なのです.
- 代数的閉体はこれ以上,代数的に拡大できません.
- 代数的閉体上の多項式
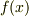 に対し,
に対し, 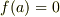 を満たす数
を満たす数  (つまり方程式の解)は,全て代数的閉体に含まれます.
(つまり方程式の解)は,全て代数的閉体に含まれます. - 代数的閉体上の多項式
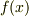 は,代数的閉体上,一次式の積の形に因数分解できます.
は,代数的閉体上,一次式の積の形に因数分解できます.
次の定理も重要です
Important
有限体は代数的閉体にはなりません.
proof
有限体 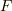 の位数を
の位数を 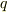 とすると,
とすると, 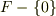 は
は  次の巡回群となり,
次の巡回群となり, 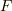 の任意の元は
の任意の元は 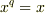 を満たします.すると,例えば
を満たします.すると,例えば 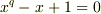 を満たす解は存在しません.よって有限体は代数的閉体にはなりえません.■
を満たす解は存在しません.よって有限体は代数的閉体にはなりえません.■
ある体の拡大体が代数的閉体になっているとき,その拡大体を 代数的閉包 と呼びます. 複素数体は,有理数体や実数体の代数的閉包です.