代数的拡大体と最小多項式
代数方程式を体論で考えるとき,この代数的拡大体という概念が一番大事です.気合を入れて取り掛かってください!!まず,体  に幾つかの元を添加して,拡大体
に幾つかの元を添加して,拡大体 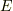 を作ることを考えます.
を作ることを考えます.
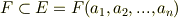
もしも, 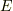 に含まれる全ての元が,
に含まれる全ての元が,  上の方程式の解になっているならば,
上の方程式の解になっているならば, 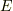 を
を  の 代数的拡大体 と呼びます.『
の 代数的拡大体 と呼びます.『  上の方程式の解になっている』というのは,つまり『その元を解とする代数方程式で,係数
上の方程式の解になっている』というのは,つまり『その元を解とする代数方程式で,係数  である方程式がなにかしら存在する』という主張です.
である方程式がなにかしら存在する』という主張です.
ここで注意しなければならないのは,ある数が代数的数であることと,拡大体が代数的であることとは少し異なる概念だということです.ある数が代数的数であるとは,その数を解とする 有理係数の代数方程式が存在する ことでした.  上の代数拡大体の定義,すなわち,拡大体の任意の元を解とする F係数の代数方程式が存在する ことと比べてみましょう.もう気づいたかと思いますが,
上の代数拡大体の定義,すなわち,拡大体の任意の元を解とする F係数の代数方程式が存在する ことと比べてみましょう.もう気づいたかと思いますが,  が有理数体ではない場合,必ずしも代数的拡大体の元が全て代数的数になるとは限りません.
が有理数体ではない場合,必ずしも代数的拡大体の元が全て代数的数になるとは限りません.
例えば 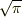 は
は 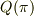 上の代数方程式
上の代数方程式 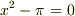 の解ですから,
の解ですから, 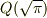 は
は 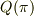 の代数的拡大体になっています.しかし,
の代数的拡大体になっています.しかし,  は超越数ですから,
は超越数ですから, 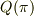 や
や 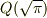 の元が必ずしも代数的数だとは言えません.代数的拡大とは,あくまでも拡大の仕方に関する概念であって,そこに含まれる元が代数的であるかを規定する概念ではないのです.用語が紛らわしいですが,せっかくなので正確に定義を覚えましょう.
の元が必ずしも代数的数だとは言えません.代数的拡大とは,あくまでも拡大の仕方に関する概念であって,そこに含まれる元が代数的であるかを規定する概念ではないのです.用語が紛らわしいですが,せっかくなので正確に定義を覚えましょう.
| [*] | 体の元が代数的であるとは,その元が 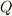 上の代数方程式の解になっているということでした.上で例に挙げた 上の代数方程式の解になっているということでした.上で例に挙げた 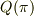 や や 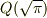 は, は, 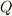 の代数的拡大体になっていませんので代数的ではない元が含まれたわけですが, の代数的拡大体になっていませんので代数的ではない元が含まれたわけですが, 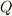 の代数的拡大体として得られる体の元は全て代数的数になります.拡大体の昇鎖列(包含関係の列)が の代数的拡大体として得られる体の元は全て代数的数になります.拡大体の昇鎖列(包含関係の列)が 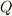 とつながっていない場合に注意が必要だということです. とつながっていない場合に注意が必要だということです. |
| [†] | 体  の拡大体 の拡大体 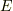 の元の中に, の元の中に,  上の代数方程式の解にならないものが含まれるとき,これを超越的拡大体と呼びます.例えば 上の代数方程式の解にならないものが含まれるとき,これを超越的拡大体と呼びます.例えば 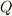 の拡大体 の拡大体  は超越的拡大体です.一般に超越数の話は難しく,この記事でも代数的拡大体の話題だけを取り上げます. は超越的拡大体です.一般に超越数の話は難しく,この記事でも代数的拡大体の話題だけを取り上げます. |
最小多項式
体  から代数的拡大体
から代数的拡大体 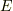 を作ります.このとき
を作ります.このとき 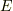 の元は全て,何らかの
の元は全て,何らかの  上の代数方程式の解になっているはずですが,このような代数方程式は無数にあります.
上の代数方程式の解になっているはずですが,このような代数方程式は無数にあります.
| [‡] | 例えば  は は 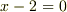 の解ですが, の解ですが, 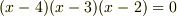 の解でもあります.本質的に, の解でもあります.本質的に,  は は  の部分だけから出てくるわけですが,このように関係ない因数を加えて次数を上げていけば, の部分だけから出てくるわけですが,このように関係ない因数を加えて次数を上げていけば,  を解とする代数方程式自体は無限にあることが分かります. を解とする代数方程式自体は無限にあることが分かります. |
拡大体 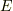 の元
の元 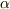 を元とする
を元とする  上の代数方程式の中で,特に次数が最低のものを,
上の代数方程式の中で,特に次数が最低のものを, 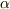 の 最小多項式 と呼びます.最小多項式には次の重要な性質があります.
の 最小多項式 と呼びます.最小多項式には次の重要な性質があります.
- 最小多項式は
 上既約です.
上既約です. - 最小多項式は
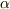 を解とする,
を解とする,  上の全ての多項式を割ることが出来ます.
上の全ての多項式を割ることが出来ます.
これらの性質は,上の注に補足したイメージを持っていれば明らかでしょう.最小多項式を 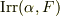 のように書きます.『
のように書きます.『 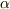 の
の  上の最小多項式』と読みます.
上の最小多項式』と読みます.
| [§] | ただし,定数倍だけ異なるものを別の多項式と見なすなら,最小多項式も無数にあることになります.例えば 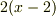 と と 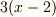 は どちらも は どちらも  の最小多項式です.あまり,こういう細かいことにはこだわらないことにしましょう. の最小多項式です.あまり,こういう細かいことにはこだわらないことにしましょう. |
最小多項式に関連した定理として,次のものが重要です.
theorem
体  の代数的拡大体を
の代数的拡大体を 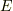 とし,
とし, 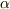 を
を  の元とします.
の元とします. 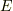 の部分体の中で,
の部分体の中で,  と
と  を含む最小の部分体を
を含む最小の部分体を 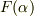 とします.
とします. 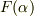 は
は  上のベクトル空間です.
上のベクトル空間です. 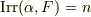 のとき,
のとき, 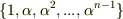 は
は 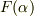 の基底になります.
の基底になります.
ここで 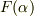 は,
は,  と
と 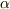 を単に合わせただけの集合ではありません.
を単に合わせただけの集合ではありません.  の元と
の元と 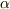 を四則演算することで出てくる新たな元を全て含みますから,もっと広がりが出てきます.『何と何を足したか』という観点で見るときりがないので,『
を四則演算することで出てくる新たな元を全て含みますから,もっと広がりが出てきます.『何と何を足したか』という観点で見るときりがないので,『 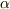 を含む
を含む 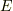 の部分体全ての共通部分』として,
の部分体全ての共通部分』として, 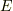 を削っていくようにして考えるのが良いでしょう.
を削っていくようにして考えるのが良いでしょう.
この定理の証明は大事なのですが,とても長いのでひとまず省略して先へ進ませて下さい.(読者の要望が多ければ,証明を書くことも検討しますのでご意見をお寄せ下さい.)
この定理によって, 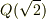 の元が
の元が  の形に書けること,
の形に書けること,  (
( 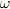 は
は 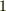 の三乗根)の元が
の三乗根)の元が 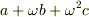 の形に書けること等が,よく納得できます.
の形に書けること等が,よく納得できます.
有限次拡大
体  の拡大体を
の拡大体を 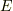 とします.
とします. 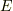 の
の  上の拡大次数
上の拡大次数 ![[E:F]](./8595ba70325b37f8f3b5c90cda4e5059.png) を考えましょう.いま
を考えましょう.いま ![[E:F]](./8595ba70325b37f8f3b5c90cda4e5059.png) が有限だとします.(
が有限だとします.( ![[E:F]](./8595ba70325b37f8f3b5c90cda4e5059.png) は
は 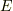 を
を  上のベクトル空間と考えたときのベクトル空間の次元でした.つまり,いま
上のベクトル空間と考えたときのベクトル空間の次元でした.つまり,いま 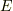 が有限ベクトル空間だと仮定したわけです.)
が有限ベクトル空間だと仮定したわけです.)
![[E:F]=n < \infty](./0127f19fca65f8b2bbcb4a79f4878ea1.png)
このとき, 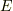 の元
の元  に対し
に対し 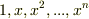 は
は 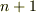 個の元ですので,
個の元ですので,  上一次従属になるはずです.つまり,零ではない
上一次従属になるはずです.つまり,零ではない  上の係数
上の係数 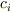 を使って,
を使って, 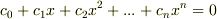 と表わすことが出来ます.これは代数方程式ですので,
と表わすことが出来ます.これは代数方程式ですので,  は
は  上代数的であり,
上代数的であり, 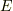 は
は  の代数的拡大体になっていることが分かりました.
の代数的拡大体になっていることが分かりました.
対偶をとって,もしも ![[E:F]=\infty](./deea8651d30495eb83a6532e0d0900ea.png) ならば,
ならば, 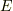 は
は  の代数的拡大体ではない,つまり超越的拡大体であることも示せます.
の代数的拡大体ではない,つまり超越的拡大体であることも示せます.
theorem
次数が有限の拡大体は代数的拡大体です.次数が無限の拡大体は超越的拡大体です.
この定理は非常に強力です.例えば,拡大体の列 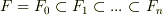 を考えるとき,
を考えるとき, 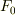 と
と 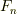 の中間体は全て有限次拡大ですので,代数的だと言えます.
の中間体は全て有限次拡大ですので,代数的だと言えます.
ここまでに出てきた定理を使う次の定理が証明できます.複素数の中には代数的数と超越数があるという主張です.
theorem
全ての代数的数を集めると,複素数の部分体になります.
証明は 数の階層 の記事で掲げます.この定理の重要な点は,複素数体の中に代数的数ではない部分があること,すなわち超越数の存在が暗示されていることです.