既約と可約
代数学の基本定理により,全ての代数方程式は複素解 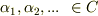 を使えば,次式のように一次式の積の形で表現できることが保証されました.
を使えば,次式のように一次式の積の形で表現できることが保証されました.
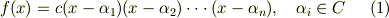
ここで, 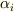 の中に同じものが含まれていても構いません( 重解 と呼ばれます).方程式を解くことは,多項式を一次式の積の形に因数分解することに他なりませんので,ある多項式が与えられたとき,まずその方程式が因数分解可能かどうかを知ることが重要です.
の中に同じものが含まれていても構いません( 重解 と呼ばれます).方程式を解くことは,多項式を一次式の積の形に因数分解することに他なりませんので,ある多項式が与えられたとき,まずその方程式が因数分解可能かどうかを知ることが重要です.
| [*] | 複素数体上で必ず一次式の積に分解できるのは,一変数の多項式に限ります.例えば, 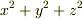 をこれ以上の因数分解することは複素数体上でも不可能です. をこれ以上の因数分解することは複素数体上でも不可能です. |
既約と可約
方程式を因数分解すると書きましたが,もちろんどの体上に方程式を考えているかによって因数分解の可能性は変わってきます.例えば 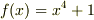 は有理数体上では因数分解不能ですが,拡大体
は有理数体上では因数分解不能ですが,拡大体 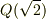 上の多項式を考えれば
上の多項式を考えれば 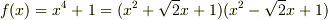 と,更なる因数分解が可能です.さらに複素数体上の多項式を考えれば
と,更なる因数分解が可能です.さらに複素数体上の多項式を考えれば 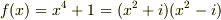 という因数分解も可能でしょう.
という因数分解も可能でしょう.
そこで,一口に因数分解と言っても,どの体上の多項式による因数分解を考えているのかを明示しなければ片手落ちです.多項式 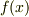 が体
が体 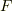 上のある多項式
上のある多項式 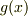 によって割り切れるとき『
によって割り切れるとき『 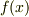 は
は 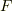 上 可約 である』と言います.
上 可約 である』と言います.
逆に, 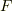 上の多項式で割ることのできない多項式を『
上の多項式で割ることのできない多項式を『 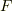 上 既約 である』と言います(ただし,どのような多項式も多項式自身と,
上 既約 である』と言います(ただし,どのような多項式も多項式自身と, 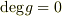 となる多項式(つまり定数)で割ることは出来ますので,これらで割る場合を除外します).
となる多項式(つまり定数)で割ることは出来ますので,これらで割る場合を除外します).
既約な多項式とは,その体上では,これ以上因数分解できない多項式です.
| [†] | 方程式の既約の定義は,素因数分解における素数の定義に少し似ています.少し意外な感じがするかも知れませんが,非常に次数の高い多項式でも既約なものがたくさんあります.素数も無限にあることが知られています.このあたりの事情も少し似ています. |
練習問題
体 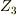 (
( 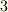 の剰余体)上の多項式で,次数
の剰余体)上の多項式で,次数 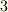 で既約なものを全て求めてみましょう.(ヒント:多項式の係数は
で既約なものを全て求めてみましょう.(ヒント:多項式の係数は ![[0],[1],[2]](./0b6f7176f189a4439c76147a8701f22a.png) のいずれかになります.)
のいずれかになります.)
幾つかの定理
重要な定理を幾つか紹介しておきます.
theorem
体 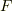 上で既約な方程式が
上で既約な方程式が 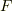 上に解を持つのは,次数が
上に解を持つのは,次数が 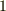 の場合に限ります.
の場合に限ります.
proof
次数が 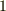 ということは,
ということは, 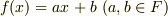 という形の方程式だということです.この解は
という形の方程式だということです.この解は 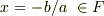 です.逆に,もし
です.逆に,もし 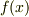 が
が 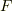 上に解
上に解 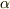 を持つとすれば
を持つとすれば 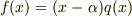 と因数分解できるはずですが,
と因数分解できるはずですが, 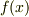 は既約ですので
は既約ですので 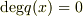 となります.すなわち
となります.すなわち 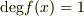 しかありえず,それは
しかありえず,それは 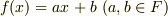 という形の方程式です.■
という形の方程式です.■
この定理と代数学の基本定理から,『複素数体上で既約な多項式は,次数が 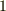 のものだけである』という定理も導けます.また,この定理により, 方程式を解くということは,方程式を一次式の積だけに因数分解することと同値である ことが確認できます.
のものだけである』という定理も導けます.また,この定理により, 方程式を解くということは,方程式を一次式の積だけに因数分解することと同値である ことが確認できます.
二つの整数が最大公約数を持つのと同様に,多項式の間にも 最大公約元 を定義できます.最大公約多項式と呼んでもいいでしょう.ただし,煩瑣なことですが,ある最大公約元と定数倍だけ異なる多項式はやはり最大公約元になります(例えば,ある二つの多項式の最大公約元が 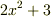 であったとすると,もとの二つの多項式を
であったとすると,もとの二つの多項式を  や
や 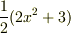 で割ることも出来ます).そこで,正確には最大公約元として定数倍だけ違った元を全てを含む集合を考えます.
で割ることも出来ます).そこで,正確には最大公約元として定数倍だけ違った元を全てを含む集合を考えます.
theorem
体 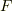 上の多項式
上の多項式 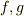 の最大公約元を
の最大公約元を 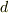 とするとき,ある多項式
とするとき,ある多項式  が
が 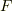 上に存在して,
上に存在して, 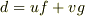 と書けます.
と書けます.
この定理の証明は省略します.整数の最大公約数に関して全く同じような定理がありますので,あまり目新しくは感じなかった人も多いでしょう.この定理を使うと,次の定理を示せます.
theorem
体 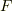 上で既約な多項式
上で既約な多項式 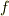 が,
が, 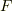 上の多項式
上の多項式 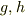 の積
の積 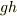 を割る場合,
を割る場合, 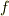 は
は 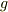 を割るか,
を割るか,  を割るか,またはその両方を割ります.
を割るか,またはその両方を割ります.
proof
もし 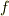 が
が 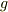 を割らないとすると,
を割らないとすると, 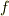 と
と 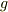 の最大公約倍数は定数だけになります.先ほどの定理より,
の最大公約倍数は定数だけになります.先ほどの定理より, 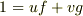 と書けるはずです.このとき両辺に
と書けるはずです.このとき両辺に  を掛ければ
を掛ければ 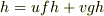 となりますので,
となりますので, 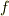 が
が 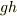 を割ることを思い出せば,右辺より
を割ることを思い出せば,右辺より 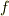 は
は  を割ることが示せます.■
を割ることが示せます.■
theorem
既約な代数方程式は,重解を持ちません.
proof
体 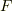 上既約な多項式
上既約な多項式 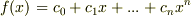 を考えます.もしも
を考えます.もしも 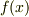 が
が 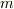 重解
重解 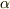 を持つとすると,
を持つとすると, 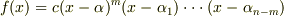 と書けるはずです.これは,
と書けるはずです.これは, 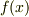 が
が  で可約だということを意味しますから,既約な多項式だという仮定に反します.■
で可約だということを意味しますから,既約な多項式だという仮定に反します.■
重解があると,『一次式の積だけ』ではなくなってしまうわけです.
| [‡] | ただし,後述しますが,体には 標数 という概念があり,標数が零でない体では,既約な代数方程式が重解を持つ場合があります.このあたりの説明が前後してしまうのは心苦しいのですが,最初から標数の話をすると難しいので,後回しにした次第です.しかも,標数が零でない体はしばらく考えませんので,標数の重要度は低いと考えました.有理数体,実数体,複素数体などの標数は零ですので,正確を期したい人は『有理数体,実数体,複素数体など,標数が零の体上で既約である⇔重根を持たない』と覚えておいて下さい(>_<). |