標数
体の拡大に関連して,幾つか重要な概念や用語を紹介します.この記事の内容は,基本的には 素体 の続きです.
標数が零でない体ではちょっと不思議な計算が行われますから,体をより深く理解するには重要な概念だと思います.しかし,標数が零でない体を考えるのは,この記事と次の 分離拡大体 だけで,それ以降は基本的に標数が 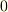 の体ばかりを扱います.ですから,少し難しい部分もあると思いますが,ここで
の体ばかりを扱います.ですから,少し難しい部分もあると思いますが,ここで  %分からなくても大丈夫です.
%分からなくても大丈夫です.
先を急ぐ読者の人は,この記事と分離拡大体は読み飛ばしても大丈夫でしょう.
標数
体 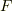 に,正の整数
に,正の整数 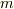 があり,任意の元
があり,任意の元 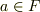 に対して
に対して  がなりたつとします.このような
がなりたつとします.このような 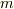 で最小のものを 体の標数 と呼びます.
で最小のものを 体の標数 と呼びます.
有理数体,実数体,複素数体では,このような 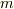 は
は  だけですから,これらの体の標数は
だけですから,これらの体の標数は 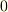 です.この定義だけでは,標数が
です.この定義だけでは,標数が 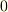 ではない体がどんなものか想像しにくいと思いますが,例えば 体 の例7で取り上げたブール体では,
ではない体がどんなものか想像しにくいと思いますが,例えば 体 の例7で取り上げたブール体では, 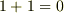 と演算を決めましたので標数は
と演算を決めましたので標数は 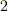 になります.このように,整数の剰余体や, 剰余体に同型な体* には,一般的に零でない標数があります.
になります.このように,整数の剰余体や, 剰余体に同型な体* には,一般的に零でない標数があります.
素数 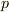 に対する整数の剰余体
に対する整数の剰余体 ![Z_{p}=\{ [0],[1],[2],....,[p-1] \}](./5bb01776694894a350c666dc9dec096e.png) の標数は
の標数は 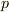 です.どの元に対しても,
です.どの元に対しても, 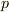 を掛ければ
を掛ければ ![p[k] = [0] \ (k=1,2,...,p-1)](./d81954931a841a8015308d15c76897e7.png) がなりたつからです.逆に言えば,任意の素数
がなりたつからです.逆に言えば,任意の素数 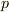 に対して,標数
に対して,標数 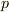 の体が一つ存在します.
の体が一つ存在します.
| [*] | 標数が零でない体上では,要するに 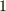 を幾つか足していくと, を幾つか足していくと, 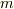 回足したところで 回足したところで 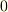 になってしまうわけです.これは,普通に知っている数の性質から言えば,極めて異常なことです.このあと 分離拡大体 では,このような算法規則が方程式論に与える影響を考えます.やはり,今まで慣れていた方程式の性質とは違うので,少し驚くことと思います.しかし,ガロア理論の章では基本的に標数 になってしまうわけです.これは,普通に知っている数の性質から言えば,極めて異常なことです.このあと 分離拡大体 では,このような算法規則が方程式論に与える影響を考えます.やはり,今まで慣れていた方程式の性質とは違うので,少し驚くことと思います.しかし,ガロア理論の章では基本的に標数 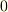 の体しか考えません.標数を考え出すと話が全てややこしくなりますから,初学者の間は抽象的な理解を深めるための頭の体操程度に思って読む程度で良いと思います. の体しか考えません.標数を考え出すと話が全てややこしくなりますから,初学者の間は抽象的な理解を深めるための頭の体操程度に思って読む程度で良いと思います. |
体の含む素体で決まる標数
体 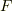 が素体
が素体 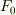 を含むとします. 素体 の記事の最後で『任意の体は唯一つだけ素体を含む』という定理を証明しました.つまり,ある体に対して,素体が一つ決まります.
を含むとします. 素体 の記事の最後で『任意の体は唯一つだけ素体を含む』という定理を証明しました.つまり,ある体に対して,素体が一つ決まります.
さて,もう一つ『任意の素体は,有理数体 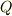 (標数
(標数 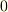 )か,剰余体
)か,剰余体 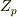 (標数
(標数 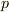 )に同型である』という定理がありました.これらを使うと, 任意の体の標数は,素体の標数で表せる ことになります.
)に同型である』という定理がありました.これらを使うと, 任意の体の標数は,素体の標数で表せる ことになります.
| [†] | 素体は,体の部分群の中で最小のものです.また,前節で標数の定義として,体の元  にたいし, にたいし,  を満たす「最小のものを」標数とすると定義しました.この定義を『素体の標数を体の標数とする』と定義する立場だと読み換えることも出来ます. を満たす「最小のものを」標数とすると定義しました.この定義を『素体の標数を体の標数とする』と定義する立場だと読み換えることも出来ます. |
体の構造に関して,素体,標数など新しい概念が急に色々と出てきましたが,次に紹介する定理によって,これらの概念が組み合わさり,素体や標数が体の構造を特徴付けるのに重要な概念であることが見えてきます.繰り返しになりますが,体の拡大をベクトル空間だと見ると定理の意味が直観的に少し分かりやすくなると思います.
有限体の位数
元の数が有限である体を 有限体 と呼びます.有理数体,実数体,複素数体などはどれも 無限体 ですので,いままで有限体はあまり出てきませんでした.有限体になりたつ美しい定理を二つ紹介します.どちらも重要な定理です.
theorem
有限体 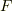 の位数を
の位数を 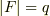 ,標数を
,標数を 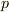 , 素体を
, 素体を 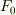 とします.
とします. ![[F:F_{0}]=n](./ce57aaeab5e44b034f5ef53dad4a8e0c.png) のとき,
のとき, 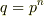 がなりたちます.
がなりたちます.
proof
素体は有理数体か剰余類体に同型ということでしたが,有理数体は無限体ですので有限体の素体になるはずがなく,素体は剰余類体に同型 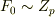 ということになります.
ということになります. 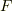 を
を 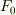 上のベクトル空間と見ることも出来ますので,
上のベクトル空間と見ることも出来ますので, 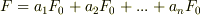 のように表すと(これが
のように表すと(これが ![[F:F_{0}]=n](./ce57aaeab5e44b034f5ef53dad4a8e0c.png) の意味することなので当然ですが),
の意味することなので当然ですが), 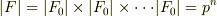 が言えます.■
が言えます.■
有限体 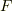 の標数を
の標数を 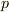 とします.ここで
とします.ここで 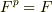 が成り立つ場合,
が成り立つ場合, 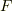 を 完全体 と呼びます.標数が
を 完全体 と呼びます.標数が 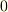 の体も完全体だとします.
の体も完全体だとします.
theorem
有限体は完全体です.
proof
写像 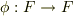 を
を 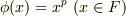 と定めると,これは単射の準同型写像となります.単射であることに注意すると,位数に関して
と定めると,これは単射の準同型写像となります.単射であることに注意すると,位数に関して 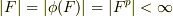 がなりたちますので,
がなりたちますので, 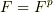 が言えます.■
が言えます.■
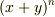 を展開すると,二項定理を使って次のように書けるのは大丈夫ですね.
を展開すると,二項定理を使って次のように書けるのは大丈夫ですね.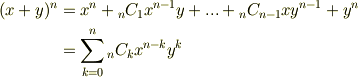
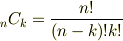
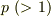 の体上で
の体上で 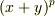 を展開すると,二項係数
を展開すると,二項係数 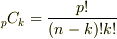 は,
は, 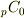 と
と 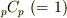 を除いて,分子に現れた
を除いて,分子に現れた 