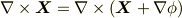管状ベクトル場
ベクトル場 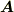 をポテンシャル関数で表わせる場合,一般にはスカラーポテンシャル
をポテンシャル関数で表わせる場合,一般にはスカラーポテンシャル 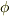 とベクトルポテンシャル
とベクトルポテンシャル 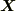 を用いて,次のように表現されます.これを ヘルムホルツの定理 と呼ぶのでした.
を用いて,次のように表現されます.これを ヘルムホルツの定理 と呼ぶのでした.

特に 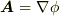 と書ける場合を 層状ベクトル場 と呼びました.この記事では,逆に
と書ける場合を 層状ベクトル場 と呼びました.この記事では,逆に 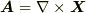 と書ける場合を考えます.
と書ける場合を考えます.
管状ベクトル場
ベクトル場 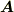 が,ベクトルポテンシャルを用いて
が,ベクトルポテンシャルを用いて 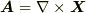 と表わせるとき,これを 管状ベクトル場
と表わせるとき,これを 管状ベクトル場 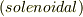 と呼びます.管状ベクトル場では, divrot=0 の関係式より,至るところ
と呼びます.管状ベクトル場では, divrot=0 の関係式より,至るところ 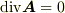 が成り立っています.発散が無いということは『流量が途中で増えたり減ったりすることが無い』ということですから,場の中に任意にとった流管内の流量は一定になります.恐らくこれが,『ホースの中の流れ』というイメージを喚起するので,管状ベクトル場と呼ぶのでしょう.(このイメージについては, ベクトル場の流束と流管 も参照してみて下さい.)
が成り立っています.発散が無いということは『流量が途中で増えたり減ったりすることが無い』ということですから,場の中に任意にとった流管内の流量は一定になります.恐らくこれが,『ホースの中の流れ』というイメージを喚起するので,管状ベクトル場と呼ぶのでしょう.(このイメージについては, ベクトル場の流束と流管 も参照してみて下さい.)
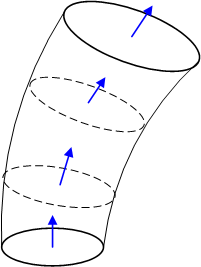
流管内は,どの断面を取っても流量が一定.
管状を,別名 回転的 と呼ぶ場合もあります.それは,場が 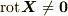 で表わされる流れによるからで,
で表わされる流れによるからで, 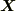 も一つのベクトル場ですから,空間内の至るところに,色々な向きや強さの回転が存在するということです.(回転の意味やイメージについては, rot と ベクトル奮闘記3 を参照下さい.)層状ベクトル場の定理と同様,管状ベクトル場には次の定理が成り立ちます.
も一つのベクトル場ですから,空間内の至るところに,色々な向きや強さの回転が存在するということです.(回転の意味やイメージについては, rot と ベクトル奮闘記3 を参照下さい.)層状ベクトル場の定理と同様,管状ベクトル場には次の定理が成り立ちます.
theorem
ベクトル場 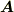 が管状であるための必要十分条件は,
が管状であるための必要十分条件は, 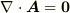 となることです.
となることです.
証明の中で, 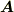 の成分
の成分 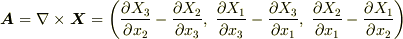 を使います.
を使います.
proof
必要条件は 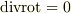 より明らかです.十分条件を証明します.
より明らかです.十分条件を証明します. 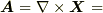 で,まず
で,まず 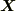 の第一成分
の第一成分 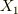 を任意の関数
を任意の関数 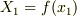 とします.また,
とします.また, 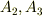 をそれぞれ
をそれぞれ 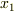 で積分して
で積分して 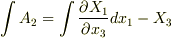 ,
, 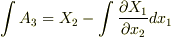 を得ます.
を得ます. 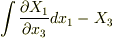 と
と 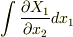 は何か適当な,
は何か適当な, 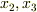 を変数とする関数と置き,
を変数とする関数と置き, 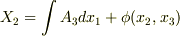 ,
, 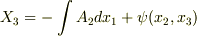 を得ます.ただし,
を得ます.ただし, 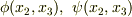 には,
には, 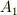 の表式
の表式 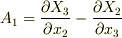 を満たす,という条件が付きます.(この条件を満たす限りで
を満たす,という条件が付きます.(この条件を満たす限りで  は任意です.)このように定めた
は任意です.)このように定めた  を使って,
を使って, 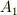 を表わすと次のようになります.
を表わすと次のようになります. 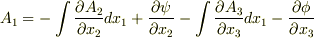
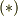 .一方,
.一方, 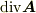 より,
より, 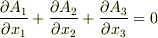 ですから,
ですから, 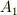 だけ移項して両辺を積分すると,
だけ移項して両辺を積分すると, 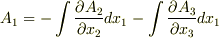 を得ます.
を得ます. 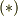 と見比べて,結局
と見比べて,結局 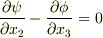 が要請されます
が要請されます 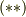 .ここまでの結果を使うと,
.ここまでの結果を使うと, 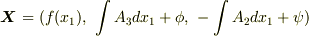 と書けます.(ただし,
と書けます.(ただし, 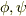 は
は 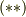 を満たすとします.)この
を満たすとします.)この 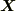 は確かに
は確かに 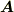 のベクトルポテンシャルになっており,定理が満たされます.■
のベクトルポテンシャルになっており,定理が満たされます.■
演習問題
ベクトル場 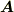 が層状のとき,
が層状のとき, 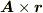 は管状になることを示して下さい.
は管状になることを示して下さい.
ベクトルポテンシャルの求め方
ベクトル場 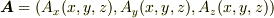 を
を 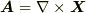 と表現できるとします.このとき,
と表現できるとします.このとき, 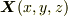 は次のように表わすことが可能です.
は次のように表わすことが可能です.
![\bm{X} = \bm{e_{x}} \left[ \int_{z_{0}}^{z} A_{2} dz \right] +\bm{e_{y}}\left[\int_{x_{0}}^{x}A_{3} dx- \int_{z_{0}}^{z}A_{1} dz \right] \tag{2}](./ff96434736d1577dac19879210ae5e36.png)
式 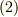 の右辺の回転を実際に取り,この形が
の右辺の回転を実際に取り,この形が 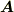 のベクトルポテンシャルになっていることを確認してみて下さい.
のベクトルポテンシャルになっていることを確認してみて下さい.
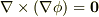 が成り立つことを考えると,ベクトルポテンシャルには,
が成り立つことを考えると,ベクトルポテンシャルには, 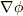 の形の差は許されることになります.
の形の差は許されることになります.