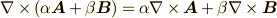rot
ここまでに,ナブラ 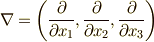 をスカラーに作用させる場合(勾配:
をスカラーに作用させる場合(勾配:  )と,ベクトルに内積を取る形で作用させる場合(発散:
)と,ベクトルに内積を取る形で作用させる場合(発散: 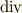 )を考えました.三次元ベクトルの場合,ナブラを 外積を取る形で作用させる ことも可能です.これを 回転 と呼び,
)を考えました.三次元ベクトルの場合,ナブラを 外積を取る形で作用させる ことも可能です.これを 回転 と呼び, 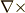 ,
, 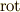 もしくは
もしくは 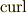 という記号で表現します.この記事では,回転について基本的な意味や性質を考えます.
という記号で表現します.この記事では,回転について基本的な意味や性質を考えます.
回転の定義
ベクトル場 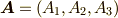 に対し,回転は次のように定義されます.
に対し,回転は次のように定義されます.
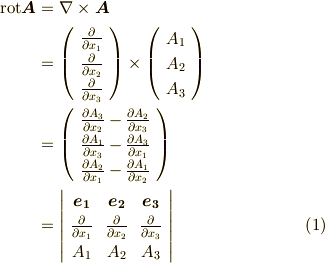
最後の行列式表示については,実際に展開して確認してみて下さい.これはあくまでも定義ですから,これで終わりです.ベクトルの外積の計算を知っている人にとって,計算自体は何も難しくないのではないでしょうか.しかし,『回転』という名前からは,何かが回転している様子を連想しますが,式 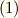 の定義式からだけでは,いったい何の回転なんだかよく分からないと思います.微分演算子とベクトル場の外積は,いったい何の回転を意味しているのでしょうか?実は,著者も,初めて勉強したときには意味がよく分かりませんでした.この記事では,次の二つのセクションで簡単説明を行います.より直観的なイメージは, ベクトル解析奮闘記 に分かりやすい絵と説明がありますので,そちらも併せて御覧ください.
の定義式からだけでは,いったい何の回転なんだかよく分からないと思います.微分演算子とベクトル場の外積は,いったい何の回転を意味しているのでしょうか?実は,著者も,初めて勉強したときには意味がよく分かりませんでした.この記事では,次の二つのセクションで簡単説明を行います.より直観的なイメージは, ベクトル解析奮闘記 に分かりやすい絵と説明がありますので,そちらも併せて御覧ください.
回転のイメージ
このセクションでは,回転の意味を直観的に理解するため,ベクトル場を水の流れの場 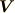 とします. ベクトル解析奮闘記 の解説によれば,回転とは『渦』を表わすということでした.では,渦が有るとか無いというのは,どういう状態なのか,もう一歩進んで考えてみましょう.紅葉が散り,川に浮かぶと,その葉の動きによって水の動きを見ることが出来ます.そんな紅葉が流されていく様子を想像してください.
とします. ベクトル解析奮闘記 の解説によれば,回転とは『渦』を表わすということでした.では,渦が有るとか無いというのは,どういう状態なのか,もう一歩進んで考えてみましょう.紅葉が散り,川に浮かぶと,その葉の動きによって水の動きを見ることが出来ます.そんな紅葉が流されていく様子を想像してください.

ちはやぶる神代もきかず竜田川からくれなゐに水くぐるとは(在原業平朝臣)
左上図のように,真っ直ぐ流れていく場合,流れに渦は無いと言います.一方,右上図のように,流れに浮かべた物がクルクル回ってしまう場合,渦があると言います.渦があるとか無いという状況は,イメージできましたか?ここで忘れてはいけないことは, 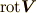 は微分形で表現されるベクトルだということです.ある点で
は微分形で表現されるベクトルだということです.ある点で 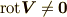 とすると,その点で渦度がある,という意味で,どんなに小さな葉っぱを浮かべようと(これが微分の考え方ですね),その点ではクルクル回ってしまうことになります.(ガウスの定理を用いて,回転を積分形で表現すると,この意味はもう少し分かりやすいと思います. divとrotの積分形による表現 を参照してください.)流れに乗って動いている葉っぱが回転してしまうという事は,葉っぱの上の方と下の方で流速に差があるということです.もしくは,本当に渦巻きのように流れが渦巻いてる場合,浮かべた葉っぱは流れては行きませんが,その場でクルクル回ることでしょう.流れの向きや強さが一様でない場合,何か
とすると,その点で渦度がある,という意味で,どんなに小さな葉っぱを浮かべようと(これが微分の考え方ですね),その点ではクルクル回ってしまうことになります.(ガウスの定理を用いて,回転を積分形で表現すると,この意味はもう少し分かりやすいと思います. divとrotの積分形による表現 を参照してください.)流れに乗って動いている葉っぱが回転してしまうという事は,葉っぱの上の方と下の方で流速に差があるということです.もしくは,本当に渦巻きのように流れが渦巻いてる場合,浮かべた葉っぱは流れては行きませんが,その場でクルクル回ることでしょう.流れの向きや強さが一様でない場合,何か 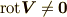 となるようです.
となるようです.

こんな流れに葉っぱを浮かべれば,クルクル回ってしまう.
渦の強さ
次図のように, 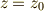 平面内に,点
平面内に,点 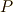 を中心に縦横の長さ
を中心に縦横の長さ 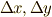 の長方形領域を考え,頂点を
の長方形領域を考え,頂点を 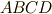 とし,頂点間の中点を
とし,頂点間の中点を 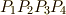 とします.
とします.
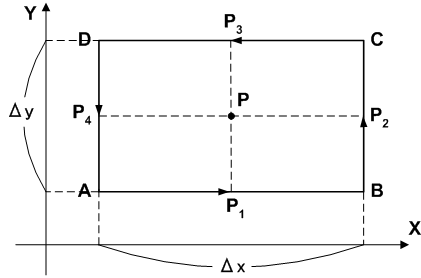
点 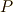 における流れを
における流れを 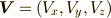 とすると,
とすると, 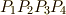 における流れは次のように表わされるでしょう.
における流れは次のように表わされるでしょう. 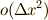 や
や  というのは,
というのは, 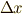 や
や 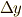 の二次以上の項という意味です.
の二次以上の項という意味です.
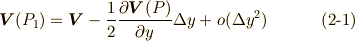


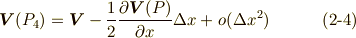
ただし,ここで 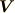 は滑らかで,必要なだけ微分可能な関数だとしています.この結果を使って,閉曲線
は滑らかで,必要なだけ微分可能な関数だとしています.この結果を使って,閉曲線 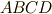 に沿った流れ成分の総和(一周)を考えます.途中で,式
に沿った流れ成分の総和(一周)を考えます.途中で,式 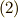 を使いますので注意していて下さい.
を使いますので注意していて下さい.

式 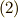 の両辺を
の両辺を 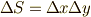 で割り,
で割り, 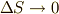 と極限を取ることで,
と極限を取ることで, 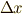 や
や 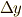 の高次項を落として次式を得ます.
の高次項を落として次式を得ます.
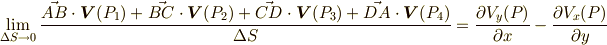
式 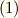 と見比べれば,これが
と見比べれば,これが 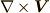 の
の  成分に等しいことが分かると思います.この結果から分かるのは,『
成分に等しいことが分かると思います.この結果から分かるのは,『 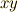 平面内で点
平面内で点 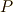 まわりに,流れの大きさを一周足し合わせたものが,
まわりに,流れの大きさを一周足し合わせたものが, 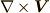 の
の  成分で表わされる』ということです.流体力学では
成分で表わされる』ということです.流体力学では  を 渦度ベクトル と呼びます.渦度ベクトルの大きさが大きければ,その分,点
を 渦度ベクトル と呼びます.渦度ベクトルの大きさが大きければ,その分,点 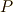 に浮かべた物は強烈にクルクル回るということになります.
に浮かべた物は強烈にクルクル回るということになります.
| [*] | 渦度の強さが,微分係数で表わされることの意味をもう一度よく考えて下さい.流れの絶対値がどんなに大きく強烈な流れであっても,それが一方向の一様な流れなら,何かをクルクル回す力はありません.単に押し流すだけです.何かを強烈にクルクル回すには,流れに浮かべた物体の上端と下端(もしくは右端と左端)といった反対の位置での流れが,『どれほど強烈に逆向きになっているか』が重要なのです.流れが連続ならば,このことは,位置によって流れが猛烈に向きを変える,ということですから,変化率(つまり微分係数)が回転の強さの指標になるというのはもっともな定義に思えます. |
回転のイメージが,少し固まってきましたか?理解を深めるには,実際に色々考えながら計算をしてみるのが一番良いと思います. 渦度ベクトルと循環 では,応用編として流体力学の分野の話題になりますが,ベクトルの回転と関連する話題を取り上げてみたいと思います.
歴史
回転の記号を文字で書く場合,日本では 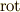 と書く人が多いようですが,これはドイツ系の数学者達が始めた記法のようです.(本当はローテーションではなくて,ロタツィオーンと読むべきなのかも知れません.)英米では
と書く人が多いようですが,これはドイツ系の数学者達が始めた記法のようです.(本当はローテーションではなくて,ロタツィオーンと読むべきなのかも知れません.)英米では 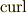 を使う人が多いです.この記法は電磁気学の マックスウェル(
を使う人が多いです.この記法は電磁気学の マックスウェル(  )が考え出したものです.マックスウェルは,テイト(
)が考え出したものです.マックスウェルは,テイト(  )と交わした往復書簡の中で,嬉しそうに次のように語っています.
)と交わした往復書簡の中で,嬉しそうに次のように語っています.
`` ... the vector part I would call the Twist of the vector function. Here the word twist has nothing to do with a screw or helix. If the word turn or version would do they would be better than twist, for twist suggests a screw. Twirld is free from the screw notion and is sufficiently racy. Perhaps it is too dynamical for pure mathematicians, so for Cayley's sake I might say Curl (after the fashion of Scroll)..."
『...(四元数の積の)ベクトル部分は「ひねり」と呼ぼうと思う.ここで言う「ひねり」という言葉は,ネジや螺旋とは一切関係ない.しかし,「ひねり」と言うとどうしてもネジを連想してしまうから,「方向転換」「偏向」といった単語の方が良いかも知れないね.「グルグル」と言えば,ネジも連想しないし,なかなか味のある名前だけど,純粋数学者にとっては,少し動的に響きすぎるかも知れない.ケーリーのためにも(スクロールの流儀にならって)「クルクル」と呼ぼうか.』(  訳)
訳)
訳の部分は,「回転」という単語を避けたため,苦労した割に訳のわからないことになってしまいました(涙).マックスウェルが類語辞典にでも出ていそうな単語を並べて命名を楽しんでいる様子が想像できますね.最後のスクロールという部分ですが,ケーリー(  )は新しい専門用語を一般的な日常用語から作る方法を取っており,代数幾何に出て来る概念に,渦巻きという意味の日常語であるスクロールを当てました.この流儀を踏襲して,という意味のようです.ケーリーが巻き毛だったとか,そういう意味ではありません.
)は新しい専門用語を一般的な日常用語から作る方法を取っており,代数幾何に出て来る概念に,渦巻きという意味の日常語であるスクロールを当てました.この流儀を踏襲して,という意味のようです.ケーリーが巻き毛だったとか,そういう意味ではありません.

弦楽器の頭部もスクロールと呼ぶ.