ベクトル解析奮闘記3
大学に入ると”ベクトル解析”を習うのですが,高校でやる”ベクトル”よりも ちょっと手ごわそうです.黒板に先生が書いた式も,難しそうだし・・・. もしよろしかったら私と一緒にベクトル解析の基本,やってみませんか.
(続き物なので ベクトル解析奮闘記1 からお読みいただくと嬉しいです!)
自宅で復習(rotの巻)
いよいよ最後, 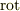 .読みは”ローテーション”(
.読みは”ローテーション”( 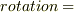 回転).
先生が黒板に書いた式は・・・,う〜ん,
これは
回転).
先生が黒板に書いた式は・・・,う〜ん,
これは 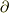 ばっかりで,
ばっかりで,  よりも
よりも 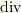 よりも,一層難しそうな顔をしている・・・.眺めていてもわからないので,先生が言われた”渦(うず)の事ですよ!”をヒントに,考えてみる事にしました.
よりも,一層難しそうな顔をしている・・・.眺めていてもわからないので,先生が言われた”渦(うず)の事ですよ!”をヒントに,考えてみる事にしました.
小川の流れをヒントに
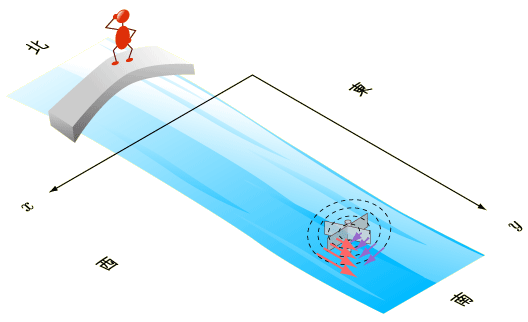
北から南に流れている小川があったとして,私が橋の上から南(下流)を見ていたとしましょう(下図参照).
普通のイメージでは,さらさらと渦など作らずに,東の岸付近の水も,西の岸付近の水も,平行に流れて行きますよね(もうすでに頭の中で渦が巻いている方もいらっしゃるでしょうか・・・).さて平行なはずの水流が,一体どうなれば渦を巻くのでしょう?まず東から西の方向・向きを  軸, 北から南(水流と平行)に行く方向・向きを
軸, 北から南(水流と平行)に行く方向・向きを 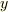 軸とします.もし東から西に行くほど(
軸とします.もし東から西に行くほど(  軸を正に行けば行くほど) 小川の流れが速いとすると,なんだか反時計回りに回り込んで,渦を巻きそうです.これは
軸を正に行けば行くほど) 小川の流れが速いとすると,なんだか反時計回りに回り込んで,渦を巻きそうです.これは  の増加に対応する
の増加に対応する 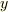 方向速度成分(
方向速度成分( 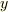 方向の矢印の長さ.速度を長さで表しているだけで,長さの分,南に動くとは限らないし,もちろん
方向の矢印の長さ.速度を長さで表しているだけで,長さの分,南に動くとは限らないし,もちろん 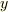 の値ではない.)の変化率が正という事です.水流の速度を表すベクトル関数を
の値ではない.)の変化率が正という事です.水流の速度を表すベクトル関数を
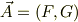
とすると, 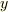 方向成分は,スカラー関数
方向成分は,スカラー関数 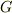 で表されるから,
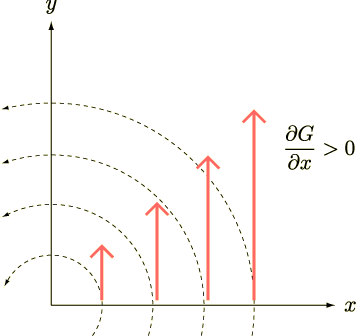
で表されるから,
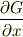
が正で,なおかつこの値が大きければ大きいほど渦は強そうですね(下図参照).
でもそれだけでいいんでしょうか?
まてよ,もしかしたら,下流の方が上流より,東から西方向(小川の流れに直交する方向)への速度があるかもしれません.もしそうなら,さっきとは丁度逆に,時計回りの渦を作りそうです.これは,”下流に行く( 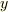 が増加する) ”ほど,”東西方向の流れが速くなる(
が増加する) ”ほど,”東西方向の流れが速くなる( 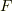 が増加する)”わけですから,同様に数式で表すと
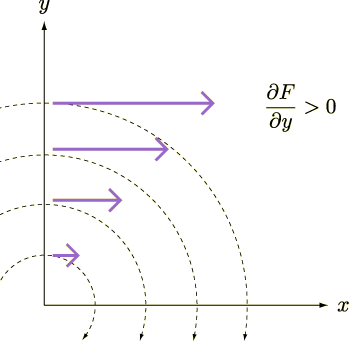
が増加する)”わけですから,同様に数式で表すと
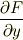
となります(下図参照).
従って,反時計回り方向の渦は,それを差し引いた分,
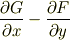
が正で,値が大きければ大きいほど,強くおこりそうです.
渦の方向・向き
ところでこの渦,どの方向に向いていると表現したらいいのでしょうか?  軸方向?それとも
軸方向?それとも 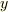 軸方向でしょうか?
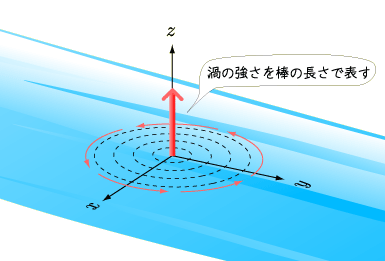
でも,見る間にぐるぐる回っているので,いずれの方向で表すのも難しそうです.むしろ渦の真中に,水面と垂直に棒を立てて目印とし,”棒を軸とした周りの渦である”とした方がわかりやすそうですね.渦の強さは棒の長さで表せば,遠目に見ても一目瞭然です(下図参照).
軸方向でしょうか?
でも,見る間にぐるぐる回っているので,いずれの方向で表すのも難しそうです.むしろ渦の真中に,水面と垂直に棒を立てて目印とし,”棒を軸とした周りの渦である”とした方がわかりやすそうですね.渦の強さは棒の長さで表せば,遠目に見ても一目瞭然です(下図参照).
 ,
, 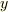 と来たので,棒の方向は
と来たので,棒の方向は  軸になります.つまり
軸になります.つまり  軸方向の渦(これ以降,回転)はさきほどの式
軸方向の渦(これ以降,回転)はさきほどの式
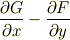
と考えられます.ここで小川のイメージから離れますが,ベクトル関数を2次元(平面)から3次元(空間)に拡張して 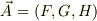 と置き,
と置き,  軸方向の回転についても,順に変数を入れ替えて,
軸方向の回転についても,順に変数を入れ替えて,
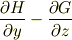
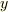 軸方向の回転についても,順に変数を入れ替えて,
軸方向の回転についても,順に変数を入れ替えて,
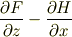
とできます.これらはそれぞれ方向の違う量なので,単純に足し算はできず,それぞれ回転の  方向成分,
方向成分, 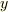 方向成分,
方向成分,  方向成分として下記のように列記するしかありません.
方向成分として下記のように列記するしかありません.
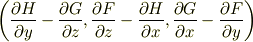
これはスカラー関数の三つ組みとも言えますが,それぞれを 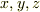 成分に持つ,3次元ベクトルとも考えられますね.このベクトルの事を
成分に持つ,3次元ベクトルとも考えられますね.このベクトルの事を 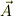 の回転(またはローテーション),記号では,
の回転(またはローテーション),記号では, 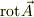 と呼ぶようです.つまり回転軸は,より回転の強い軸方向に近く向いているわけです.なお普通は,
と呼ぶようです.つまり回転軸は,より回転の強い軸方向に近く向いているわけです.なお普通は, 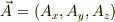 という風に表記するので
という風に表記するので
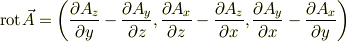
という形になります(目が回りそう・・・).
一体,何の役に?
さて,この”回転”,何に使うのでしょうか?ベクトル解析全体が,電磁気学っぽいですが,棒の周りの”回転”というと,例えば,電線に電流を流した際に,周りにできる磁界ベクトルなどを表すのに使えるそうです.磁界ベクトルを 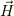 , 電流密度ベクトルを
, 電流密度ベクトルを 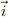 とすると,
とすると,
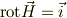
となる・・・,そうですよ.
みなさん,これからもベクトル解析,電磁気学頑張って下さいね.応援してます!(^-^) (私も頑張ります(>_<))
(続き物なので ベクトル解析奮闘記1 , ベクトル解析奮闘記2 もお読みいただくと嬉しいです!)