ヘルムホルツの定理
ベクトル場には,スカラーポテンシャルとベクトルポテンシャルという二種類の(本質的に異なる)ポテンシャル関数があるということでしたが,『どんなベクトル場も,スカラーポテンシャル場とベクトルポテンシャル場の和として表わせる』というのが ヘルムホルツの定理 と呼ばれる定理です.この定理は,電磁気学で大活躍しますので,しっかり覚えておいて下さい.ときには ベクトル解析の基本定理 とも呼ばれる大事なものです.
theorem
【ヘルムホルツの定理】連続なベクトル場 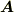 を考えます.無限遠で
を考えます.無限遠で 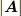 が
が 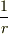 より遅くはなく
より遅くはなく 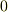 に収束し,
に収束し, 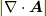 と
と 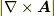 が無限遠で
が無限遠で 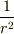 より遅くはなく
より遅くはなく 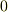 に収束する場合,
に収束する場合, 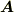 はスカラーポテンシャル場とベクトルポテンシャル場の和の形に(定数と定ベクトルを除いて)一意的に表現することが出来ます.
はスカラーポテンシャル場とベクトルポテンシャル場の和の形に(定数と定ベクトルを除いて)一意的に表現することが出来ます.

スカラーポテンシャルにマイナスをつけて 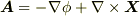 と書く人もいると思います.その方が物理的な応用には便利でしょう.しかし,数学的に,この符号には本質的な違いはありません.(詳しくは スカラーポテンシャル を参照ください.)証明はやや面倒なので後回しにし,次のように,天下り的に定理が満たされていることをとりあえずは確認しておいて下さい.
と書く人もいると思います.その方が物理的な応用には便利でしょう.しかし,数学的に,この符号には本質的な違いはありません.(詳しくは スカラーポテンシャル を参照ください.)証明はやや面倒なので後回しにし,次のように,天下り的に定理が満たされていることをとりあえずは確認しておいて下さい.
いきなりですが, 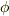 と
と 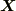 を次のようにおきます.
を次のようにおきます.
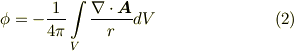
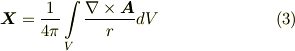
これを式 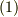 に代入すれば定理が満たされることが示されます.つまり,式
に代入すれば定理が満たされることが示されます.つまり,式 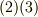 の
の 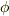 と
と 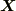 が
が 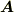 のスカラーポテンシャルとベクトルポテンシャルになります.ただし,式
のスカラーポテンシャルとベクトルポテンシャルになります.ただし,式 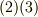 の
の 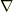 は極座標表示にしなければなりませんので,極座標における
は極座標表示にしなければなりませんので,極座標における 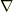 を知らない人は, ベクトルの公式2 を参照して下さい.
を知らない人は, ベクトルの公式2 を参照して下さい.
| [*] | ここで示したのは,少なくとも一つはスカラーポテンシャルやベクトルポテンシャルが存在する,という十分条件だけです.必要条件については,次のセクションで証明します.証明が面倒な人も,とりあえずこの結果だけは覚えておくようにして下さい. |
| [†] | 定理の中で,『(定数と定ベクトルを除いて)一意的に』と書いたのは,ベクトルポテンシャルに対し,任意の関数 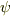 を使って を使って 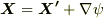 としても としても 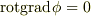 より結果は変わりませんし,スカラーポテンシャルに より結果は変わりませんし,スカラーポテンシャルに 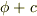 のように定数を足しても結果は変わらないという意味です. のように定数を足しても結果は変わらないという意味です. |
| [‡] | 定理の中に,『無限遠で収束云々・・・』という条件が述べられています.これは定理の成立に必要な条件なのですが,例えば電場,磁場などのベクトル場に対してヘルムホルツの定理を使おうという場合,物理的直観として,たとえこれらの場の数学的表現を知らなくても,これらの場が無限遠で十分な大きさを持つとは到底考えられません.(例えば,私達は何光年も先の星にある磁石の影響など,まったく気にせず暮らしています.)ですから,何だかややこしいことを言っているように思うかも知れませんが,実際に物理学的な状況に定理を適用する場合に,そんなに厳しい条件ではありません. |
証明
まず, rotgrad=0,divrot=0 の関係式を使うと,命題は,次の二式を満たすスカラーポテンシャル 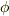 とベクトルポテンシャル
とベクトルポテンシャル 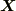 の存在を示すことに置き換えられます.
の存在を示すことに置き換えられます.

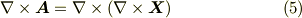
ここで,ベクトルポテンシャルには 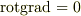 の関係より,スカラー関数の勾配に相当する差が許されます.実際,
の関係より,スカラー関数の勾配に相当する差が許されます.実際, 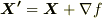 と置いても,
と置いても, 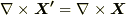 は満たされることが確認できます.このスカラー関数
は満たされることが確認できます.このスカラー関数 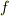 は任意ですので,
は任意ですので, 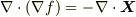 を満たす
を満たす 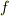 を選ぶことも可能です.言い換えれば,
を選ぶことも可能です.言い換えれば, 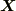 に対して,次の条件式を新たに付け加えても,定理の一般性を失いません.
に対して,次の条件式を新たに付け加えても,定理の一般性を失いません.

このような条件を付けることで,式 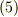 は更に次のように変形できます.
は更に次のように変形できます.
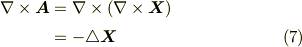
ただし,一般に成り立つ関係式 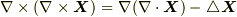 と式
と式 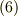 を用いて変形しました.証明の十分条件は,式
を用いて変形しました.証明の十分条件は,式 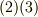 を式
を式 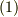 に代入することで既に示されていますので,以下では式
に代入することで既に示されていますので,以下では式 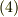 を満たすスカラーポテンシャルと,と式
を満たすスカラーポテンシャルと,と式 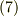 を満たすベクトルポテンシャルが存在することを個別に示すだけとします.
を満たすベクトルポテンシャルが存在することを個別に示すだけとします.
proof
【式 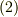 を満たすポテンシャルの存在】式
を満たすポテンシャルの存在】式 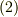 を満たす
を満たす 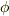 を求めるには, グリーンの定理 の系として導いた公式
を求めるには, グリーンの定理 の系として導いた公式 ![\phi (M) = -\frac{1}{4\pi} \int \int \int \limits _{V} \frac{1}{r}\triangle \phi dV -\frac{1}{4\pi}\int \int \int \limits _{S} \left[ \phi \frac{\partial }{\partial n} \left( \frac{1}{r} \right ) - \frac{1}{r} \frac{\partial \phi}{\partial n} \right] dS](./4be3a8b29c776a4e63cdfb4da3d7e2b8.png) を使います.この公式で
を使います.この公式で 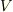 は全空間を意味し,
は全空間を意味し, 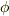 は無限遠で
は無限遠で 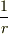 よりも早く
よりも早く 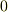 に収束するとします.このとき,
に収束するとします.このとき, 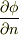 も
も 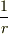 よりも早く
よりも早く 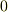 に収束し,『全空間の表面
に収束し,『全空間の表面 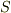 』とは無限遠のことですから(この言い方は少し数学的にいい加減ですがここでは深入りしません),第二項の面積分は
』とは無限遠のことですから(この言い方は少し数学的にいい加減ですがここでは深入りしません),第二項の面積分は 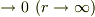 となります.よって,このようなスカラー関数
となります.よって,このようなスカラー関数 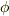 は
は 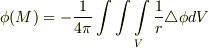 を満たすと言えます.この
を満たすと言えます.この 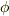 は確かに式
は確かに式 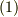 を満たし,スカラーポテンシャルになっています.(
を満たし,スカラーポテンシャルになっています.( 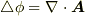 を使えば,式
を使えば,式 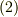 と同じです.)■
と同じです.)■
proof
【式 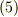 を満たすポテンシャルの存在】スカラーポテンシャルの証明と同様に, グリーンの定理 の系として導いた公式
を満たすポテンシャルの存在】スカラーポテンシャルの証明と同様に, グリーンの定理 の系として導いた公式 ![\bm{X} (M) = -\frac{1}{4\pi} \int \int \int \limits _{V} \frac{1}{r}\triangle \bm{X} dV -\frac{1}{4\pi}\int \int \limits _{S} \left[ \bm{X} \frac{\partial }{\partial n} \left( \frac{1}{r} \right ) - \frac{1}{r} (\bm{n} \cdot \nabla ) \bm{X} \right] dS](./f5418dec5482d7ca615acf503fbfdcc3.png) を使います.
を使います. 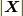 が無限遠で
が無限遠で 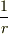 よりも早く
よりも早く 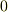 に収束すると仮定すると,この第二項は,先ほどと同じ理由で落ちるので,
に収束すると仮定すると,この第二項は,先ほどと同じ理由で落ちるので, 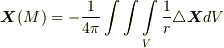 を得ます.これは確かに式
を得ます.これは確かに式 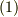 を満たし,ベクトルポテンシャルになっています.(式
を満たし,ベクトルポテンシャルになっています.(式 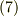 を使って
を使って 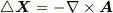 とすれば,式
とすれば,式 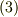 と同じです.)■
と同じです.)■
ヘルムホルツ
ヘルムホルツ(  )は,ベルリン近郊の都市ポツダムで生まれました.ヘルムホルツの父はギムナジウムの先生でしたが,一家の経済状態は苦しく,大学進学には奨学金が必要でした.当時,プロイセン政府から,卒業後
)は,ベルリン近郊の都市ポツダムで生まれました.ヘルムホルツの父はギムナジウムの先生でしたが,一家の経済状態は苦しく,大学進学には奨学金が必要でした.当時,プロイセン政府から,卒業後  年間プロイセン陸軍に軍医として勤務することを条件に医学部への奨学金制度があり,ヘルムホルツは奨学金のために,興味のあった物理ではなく,医学部へ進学しました.大学で物理や数学を勉強した形跡がないため,恐らく独学していたと思われますが,卒業後まもなく,生理学にエネルギー保存の法則を適用し,『筋肉の運動で熱が出ること』などを物理的に説明する論文を発表しました.当時,生理学に物理学的視点を持ち込むことは大変に新鮮でインパクトも大きく,これがきっかけで,プロシア陸軍を辞めて大学に戻ることが許されます.その後も,大学では生理学と解剖学を教えつつ,独自の検眼装置を発明したり,色彩や眼球の光学理論を進歩させるなど,独自の視点で研究を続けました.
年間プロイセン陸軍に軍医として勤務することを条件に医学部への奨学金制度があり,ヘルムホルツは奨学金のために,興味のあった物理ではなく,医学部へ進学しました.大学で物理や数学を勉強した形跡がないため,恐らく独学していたと思われますが,卒業後まもなく,生理学にエネルギー保存の法則を適用し,『筋肉の運動で熱が出ること』などを物理的に説明する論文を発表しました.当時,生理学に物理学的視点を持ち込むことは大変に新鮮でインパクトも大きく,これがきっかけで,プロシア陸軍を辞めて大学に戻ることが許されます.その後も,大学では生理学と解剖学を教えつつ,独自の検眼装置を発明したり,色彩や眼球の光学理論を進歩させるなど,独自の視点で研究を続けました.

ヘルムホルツは音楽と絵画と哲学を愛した.
また,流体力学や音響学の研究も重要ですが,ヘルムホルツのこの頃の研究は,何か生理学と関係がある(例えば音響学は聴覚)という点も興味深いです.音楽の理論的研究は,音楽愛好家でもあったヘルムホルツの趣味も関係していたことでしょう.  年,ベルリンの大学で念願の物理学のポストを手にし,ようやく生理学を離れて大好きな物理と数学に打ち込めるようになりました.その後のヘルムホルツは,電磁気学,熱力学などを幅広く研究しました.ヘルムホルツは幅広い教養を持ち,また,『世界は究極的に単純で美しい物理法則によって記述できるはずだ』という信念を持っていました.こうしたパラダイムは,
年,ベルリンの大学で念願の物理学のポストを手にし,ようやく生理学を離れて大好きな物理と数学に打ち込めるようになりました.その後のヘルムホルツは,電磁気学,熱力学などを幅広く研究しました.ヘルムホルツは幅広い教養を持ち,また,『世界は究極的に単純で美しい物理法則によって記述できるはずだ』という信念を持っていました.こうしたパラダイムは,  世紀に入ると量子力学の登場によって崩れます.(量子力学も美しい理論ですが,不確定性という概念が入ってきます.)この意味で,ヘルムホルツは典型的な
世紀に入ると量子力学の登場によって崩れます.(量子力学も美しい理論ですが,不確定性という概念が入ってきます.)この意味で,ヘルムホルツは典型的な  世紀の知識人でした.
世紀の知識人でした.