ガウスの発散定理の応用
この記事では, ガウスの発散定理 から導ける応用的な定理を考えます.ガウスの発散定理がよく分かってない人は,先によく復習しておいて下さい.
【ガウスの発散定理】

派生する定理1
まず,特殊な場合として,ベクトル場 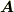 があるスカラー関数
があるスカラー関数 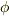 と適当な定ベクトル
と適当な定ベクトル  を使って
を使って 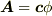 と表わせる場合を考えます.このとき,式
と表わせる場合を考えます.このとき,式 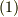 に
に 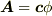 を代入すると次式を得ます.
を代入すると次式を得ます. 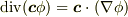 となることに注意して下さい.
となることに注意して下さい.
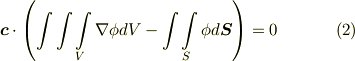
ここで  は任意のベクトルでしたので,括弧の部分
は任意のベクトルでしたので,括弧の部分 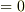 が要請されて次式を得ます.これは 面積分と体積分 で考えた公式に他なりません.(面積分と体積分の記事中では,微分の方向を
が要請されて次式を得ます.これは 面積分と体積分 で考えた公式に他なりません.(面積分と体積分の記事中では,微分の方向を 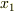 と仮定していましたが,式
と仮定していましたが,式 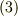 はそれが
はそれが 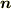 方向に一般化されています.)
方向に一般化されています.)
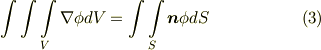
右辺で 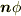 と,少し変な書き方をしましたが,これは狙いがあってのことなので後で説明します.
と,少し変な書き方をしましたが,これは狙いがあってのことなので後で説明します.
派生する定理2
次に 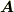 があるベクトル関数
があるベクトル関数 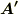 と適当なベクトル
と適当なベクトル  を使って
を使って 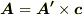 と表わせる場合を考えます.このとき,式
と表わせる場合を考えます.このとき,式 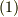 は次式のように変形できます.
は次式のように変形できます. 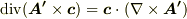 となることと,
となることと, 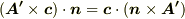 に注意して下さい.(よく分からない人は ベクトルの公式2 を参考にして下さい.)
に注意して下さい.(よく分からない人は ベクトルの公式2 を参考にして下さい.)
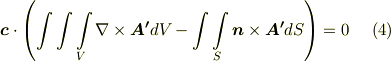
ここでも  は任意のベクトルでしたので,括弧の部分
は任意のベクトルでしたので,括弧の部分 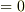 が要請されて次式を得ます.
が要請されて次式を得ます.
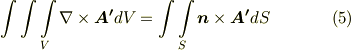
派生する定理3
ベクトル場 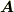 が,ある適当なベクトル
が,ある適当なベクトル  とテンソル
とテンソル 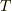 を使って次のように表現できる場合を考えます.
を使って次のように表現できる場合を考えます.

これを式  に代入し,前の二つの定理と同様の議論を用いると,
に代入し,前の二つの定理と同様の議論を用いると,  が任意のベクトルであることから次式を得ます.
が任意のベクトルであることから次式を得ます.
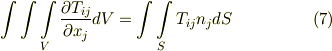
ここまで読んで,式 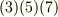 が全て似たような形をしていることに気がつくと思います.
が全て似たような形をしていることに気がつくと思います. 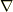 の作用の仕方が,
の作用の仕方が,  か
か 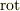 か,はたまた二階のテンソルの微分なのかという違いはありますが,全て次のような形をしています.(作用の仕方が分からないので,
か,はたまた二階のテンソルの微分なのかという違いはありますが,全て次のような形をしています.(作用の仕方が分からないので, 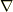 の右側は
の右側は 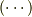 としておきます.作用の仕方は,ここに入る関数次第だということにしておきます.)
としておきます.作用の仕方は,ここに入る関数次第だということにしておきます.)
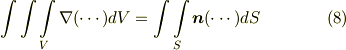
| [*] | 式 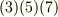 が同じ形にまとめられるのは,もちろん偶然ではありません.これらが同じ公式であることは, 微分形式の理論 を勉強するとより包括的に理解できると思います.また,この記事の兄弟版とも言える ストークスの定理の応用 も併せてご覧下さい. が同じ形にまとめられるのは,もちろん偶然ではありません.これらが同じ公式であることは, 微分形式の理論 を勉強するとより包括的に理解できると思います.また,この記事の兄弟版とも言える ストークスの定理の応用 も併せてご覧下さい. |