面積分と体積分
この記事では,体積分を面積分に直せるような特別な場合を考えます.面積分と体積分を関係付けるものとしては ガウスの発散定理 が有名で,この次に勉強しますが,この記事の内容はガウスの発散定理の準備編とも言うべきものです.特別な知識は必要としないので,気楽に読んでください.
体積分を面積分に直す
体積分の積分変数は,もちろん座標系の取り方によりますが,仮に被積分関数が,次式のように『一つの積分変数による偏微分の形』になっている場合を考えましょう.
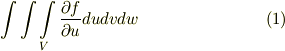
このとき,  が言えますので,実質的に積分変数を二つに減らせます.このようにして,体積分を面積分に直せるわけです.
が言えますので,実質的に積分変数を二つに減らせます.このようにして,体積分を面積分に直せるわけです.
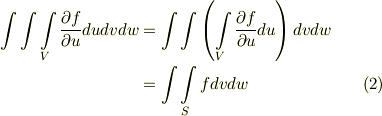
逆に言えば,被積分関数が上手く積分変数の偏微分の形にさえなっていれば,積分の次元を下げられるということです.式 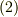 のようにして困ることは,右辺が面積分にも関わらず,面の表裏(具体的には法線ベクトルが正となる向き)に関する情報が入っていないことです.( 面積素に関して補足 参照.)無いのなら自分で決めてやらねばなりません.面積素
のようにして困ることは,右辺が面積分にも関わらず,面の表裏(具体的には法線ベクトルが正となる向き)に関する情報が入っていないことです.( 面積素に関して補足 参照.)無いのなら自分で決めてやらねばなりません.面積素 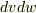 が
が 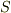 の法線となす角を
の法線となす角を 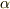 として,
として, 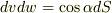 と置くしかないでしょう.
と置くしかないでしょう.
| [*] | 法線ベクトルの絶対値を取ってスカラーにしてしまうのは簡単ですが,逆に,スカラーからベクトルの向きを決めることは出来ません.向きを後付けで考えるには,適切な向きを付けられるように,図形的な考察を別途行う必要があります.これは手間ですし,もっと複雑な図形になると無理になってきます.線積分の積分経路には向きがあり,周回積分にも回る方向がありました.二次元の積分とも言うべき面積分でこの向きに相当するのが,曲面の表・裏です.曲面の表・裏を決めずして面積分は出来ません.では,体積分にはどんな向きがあるのでしょうか?体積分には,積分の方向と言うようなものはありませんが,体積素 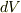 の符号は,右手系なら の符号は,右手系なら 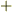 ,左手系なら ,左手系なら  というように決めます.これが体積分の向きとも言うべきものです.(これは積分の向きと言うよりは,空間の向きというべきものですね.)積分の際に,いつも向きを気にするのは面倒なことですが,積分変数( というように決めます.これが体積分の向きとも言うべきものです.(これは積分の向きと言うよりは,空間の向きというべきものですね.)積分の際に,いつも向きを気にするのは面倒なことですが,積分変数( 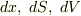 )そのものに,積分の向きを織り込んでしまったのが 微分形式 と言う形式になります.単に向き付き積分を考えるだけでなく,積分の向き,空間の向き,座標変換とは何か,といった問題について深い見通しを与えてくれる美しい理論です.ベクトル解析が終わったら,ぜひ微分形式も勉強してみて下さい. )そのものに,積分の向きを織り込んでしまったのが 微分形式 と言う形式になります.単に向き付き積分を考えるだけでなく,積分の向き,空間の向き,座標変換とは何か,といった問題について深い見通しを与えてくれる美しい理論です.ベクトル解析が終わったら,ぜひ微分形式も勉強してみて下さい. |