面積素に関して補足
面積分に出て来る微小面積要素のベクトル形 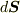 を ベクトル面積素 と呼びます.実際に面積分を計算する場合,ベクトル面積素の扱いで注意すべき点に触れます.この記事には,微分形式,曲面の第一基本量など,少し発展的な話題も出てきますが,初めてそんな言葉を聞く人は無視して先に進むようにして下さい.自分に関係ありそうな部分だけを読んで頂ければ良いと思います.
を ベクトル面積素 と呼びます.実際に面積分を計算する場合,ベクトル面積素の扱いで注意すべき点に触れます.この記事には,微分形式,曲面の第一基本量など,少し発展的な話題も出てきますが,初めてそんな言葉を聞く人は無視して先に進むようにして下さい.自分に関係ありそうな部分だけを読んで頂ければ良いと思います.
デカルト座標系の場合
面積分の積分領域 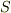 が,デカルト座標系
が,デカルト座標系 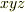 で記述されている場合,ベクトル面積素は単純に次のような微小線素
で記述されている場合,ベクトル面積素は単純に次のような微小線素 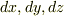 の積になります.
の積になります.
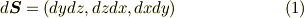
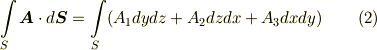
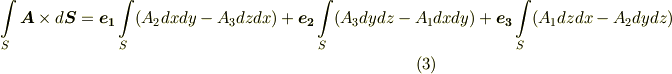
一般に,曲面の方程式が陰関数 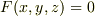 の形で与えられる場合,曲面の単位法線ベクトルは勾配を使って次のように表現できます.
の形で与えられる場合,曲面の単位法線ベクトルは勾配を使って次のように表現できます.

また, 微分形式 を知っている読者の人は,ベクトル面積素が次のように書けることも勉強されたことでしょう.この表現には,微小面積の大きさだけでなく,『曲面の向き(表・裏)』が含められています.
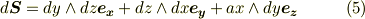
曲面がパラメーター表示されている場合
曲面 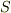 が次のように二変数ベクトル関数によってパラメーター表示されている場合を考えます.
が次のように二変数ベクトル関数によってパラメーター表示されている場合を考えます.
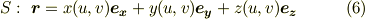
このとき, 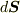 はスカラー形もしくはベクトル形で次のように表わされます.
はスカラー形もしくはベクトル形で次のように表わされます.
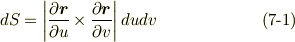
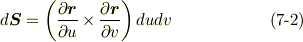
ここで,微小面積は 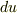 と
と 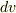 の張る平行四辺形で近似されていることに注意して下さい.また,法線ベクトル
の張る平行四辺形で近似されていることに注意して下さい.また,法線ベクトル 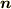 は
は 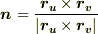 と表わせることを確認して下さい.(ただし
と表わせることを確認して下さい.(ただし 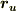 などは,
などは,  の
の  による偏微分という意味の略記とします.)もとの
による偏微分という意味の略記とします.)もとの 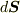 成分が
成分が 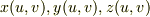 の関数として表現されていた場合,ヤコビアンを用いて次のように表現されます.
の関数として表現されていた場合,ヤコビアンを用いて次のように表現されます.
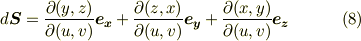
さらに,少し発展的な話題になりますが,微分幾何を勉強したことがある人は,パラメーター表示された曲面の面積素を次のように表現できることを覚えているかも知れません.
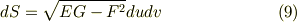
ここで, 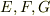 は曲面の第一基本量と呼ばれる量で,式
は曲面の第一基本量と呼ばれる量で,式 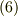 で表現される曲面に対し,次のように定義される量です.
で表現される曲面に対し,次のように定義される量です.



第一基本量を使えば,曲線の弧長要素 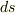 は次のように表現できます.
は次のように表現できます.
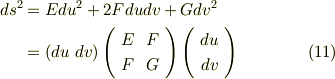
このように,面積分は一般に二変数の積分になりますから,急に色々と注意する点が出てきます.基本的に注意すべき点は,次の事柄です.
- 表と裏を区別できる曲面なのか?
- 法線ベクトルの向き(どちらを表と取るか)
- 曲面全体の形(穴が空いているか等)
線積分には始点と終点があり,積分に『向き』がありました.(周回積分でも同様に,右回りか左回りかという『向き』がありました.)面積分で曲面の表裏が重要なのは,積分領域の表裏が,積分の『向き』に相当するものだからです.三番目の,曲面の形という問題は, 積分領域について補足 で取り上げます.