ストークスの定理の応用
この記事では, ストークスの定理 から導ける応用的な定理を考えます.ストークスの定理がよく分かってない人は,まずストークスの定理をよく復習しておいて下さい.
【ストークスの定理】

ただし式中, 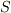 は,閉曲線
は,閉曲線 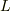 を境界とする,表裏を区別できる単連結な曲面だとし,
を境界とする,表裏を区別できる単連結な曲面だとし, 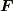 の各成分は
の各成分は 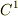 級の関数とします.また この記事の内容は"ガウスの発散定理の応用"に酷似しています (正直言えば,コピーペーストして原稿を書いた部分がたくさんあります.)全く共通な部分は,少し省いてあります.もし, ガウスの発散定理の応用 をまだ読んでない人は,そちらも併読して,比べてみるといいかも知れません.
級の関数とします.また この記事の内容は"ガウスの発散定理の応用"に酷似しています (正直言えば,コピーペーストして原稿を書いた部分がたくさんあります.)全く共通な部分は,少し省いてあります.もし, ガウスの発散定理の応用 をまだ読んでない人は,そちらも併読して,比べてみるといいかも知れません.
派生する定理1
まず,ベクトル場 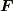 が,あるスカラー関数
が,あるスカラー関数 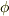 と適当な定ベクトル
と適当な定ベクトル  を使って
を使って 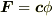 と表わせる場合を考えます.このとき,式
と表わせる場合を考えます.このとき,式 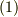 に
に 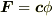 を代入すると次式を得ます.
を代入すると次式を得ます.  となることに注意して下さい.
となることに注意して下さい.
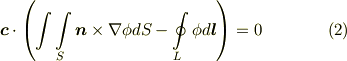
ここで  は任意のベクトルでしたので,括弧の部分
は任意のベクトルでしたので,括弧の部分 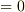 が要請されて次式を得ます.
が要請されて次式を得ます.
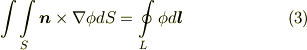
ここで 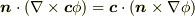 と変形しました.(よく分からない人は, ベクトルの公式2 を参考に考えてみて下さい.)
と変形しました.(よく分からない人は, ベクトルの公式2 を参考に考えてみて下さい.)
派生する定理2
次に, 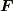 があるベクトル関数
があるベクトル関数  と適当なベクトル
と適当なベクトル  を使って
を使って 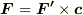 と表わせる場合を考えます.このとき,前セクションと同様の議論により,式
と表わせる場合を考えます.このとき,前セクションと同様の議論により,式 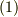 から次式を得ます.
から次式を得ます.
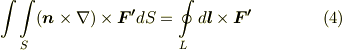
ここまで読んで,式  が似た形をしていることに気がつくと思います.
が似た形をしていることに気がつくと思います. 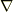 の作用の仕方が,
の作用の仕方が,  か
か 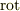 かという違いはありますが,両方とも次のような形をしています.(作用の仕方が分からないので,
かという違いはありますが,両方とも次のような形をしています.(作用の仕方が分からないので, 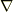 の右側は
の右側は  としておきます.作用の仕方は,ここに入る関数次第だということにしておきます.)
としておきます.作用の仕方は,ここに入る関数次第だということにしておきます.)
| [*] | この記事を読んで『「ガウスの発散定理の応用」とほとんど同じ内容じゃないか!本文も,ほとんどコピーペーストだし!この著者は何と手抜きなんだ!!』と憤激している人がいるかも知れません.いや,少し待ってください(手抜きの言い訳をします).数学の記事で,違う定理に対して同一の記述を使えるということは,これらの定理を支配している何かより根源的な原理が同一だということが示唆されていると考えられます.つまり,『何かがほとんど同じだ』ということに気がついたら,その背後に何か共通する数学的構造を予想できるわけです.ガウスの発散定理とストークスの定理という,別々に考えていた定理に明らかに共通な構造がありそうだと思いませんか? この予想は正しく, 微分形式 の理論を勉強すると,この定理が同じ定理の違った切り口に過ぎないことが分かります.そんなことを,面白く感じて頂ければ幸いです. |