変分法1
変分法という数学の分野があります.これは他の数学の分野と少し毛色の違った分野です.変分法はそれ自体で大変興味深い分野なのですが,『変分法』という独立した題目の講義がある大学は大変少ないようで,大抵は解析力学の授業で少し触れられるだけのようです.
この記事は,変分法入門という位置づけですので,読者の方々に,変分法とは何なのかを理解して頂くことを当面の目標とします.物理学の中で変分法がどのように利用されるのか,というような話題には触れません.変分問題を解くためによく使うオイラー方程式という方程式を導くところまでを,この記事でカバーします.
微分法に関する初等的な知識があると,読みやすいと思います.
変分法って何だろう?
関数 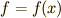 の最大・最小問題を考えるとき,一つの方法は,関数を微分し,その導関数
の最大・最小問題を考えるとき,一つの方法は,関数を微分し,その導関数 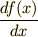 の値を調べるというものです.導関数を零にするような値
の値を調べるというものです.導関数を零にするような値  に対して,関数は最大値・最小値・変曲点のいずれかになります.このような
に対して,関数は最大値・最小値・変曲点のいずれかになります.このような  の値が分かれば,最大・最小問題は解決です.これは,微分法の話です.(ここまで読んで,なんだか難しいと感じる人は,先に微分の復習をして,頭を整理してみて下さい.)
の値が分かれば,最大・最小問題は解決です.これは,微分法の話です.(ここまで読んで,なんだか難しいと感じる人は,先に微分の復習をして,頭を整理してみて下さい.)

これと大変似たような問題なのですが,何か関数 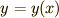 の 形 によって決まる量(関数の値ではないことに注意!)
の 形 によって決まる量(関数の値ではないことに注意!) 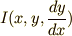 (つまり関数形の関数です.これを汎関数と呼びます)の最大・最小問題を考えるのが変分法と言われる計算です.汎関数
(つまり関数形の関数です.これを汎関数と呼びます)の最大・最小問題を考えるのが変分法と言われる計算です.汎関数 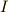 の微小な変化を零にするような関数形に対して,その汎関数は最大値・最小値・停留値のいずれかを取ることになります.求めたいのは,このような関数形
の微小な変化を零にするような関数形に対して,その汎関数は最大値・最小値・停留値のいずれかを取ることになります.求めたいのは,このような関数形  です.
です.
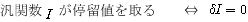
なんだか,微分と変分って,すごく似てると思いませんでしたか?言葉がごちゃごちゃしますので,表を使って,そのアナロジーを確認してみます.
| 微分 | 変分 | |
|---|---|---|
| 扱う問題 | 極値問題 | 極値問題 |
| 何の極値? | 関数 | 汎関数 |
| 変化するもの | 変数 | 関数形そのもの |
| 極値では・・・ | 微分が零になる | 変分が零になる |
いわば,変分法は『関数による関数の微分』というようなものなのです.変分法の歴史については 最速降下曲線 の記事の中にエピソードが触れてありますので,興味のある人は読んで見てください.
変分問題の解き方概論
前のセクションで,変分法は微分法に大変似ているということを見ました.微分法がよくわかっている人にとって,変分法の原理自体はそれほど難しいものではないと思います.しかし,変分法と微分法の違う部分も,しっかりと理解することが大事です.もう少し考察を深めてみます.
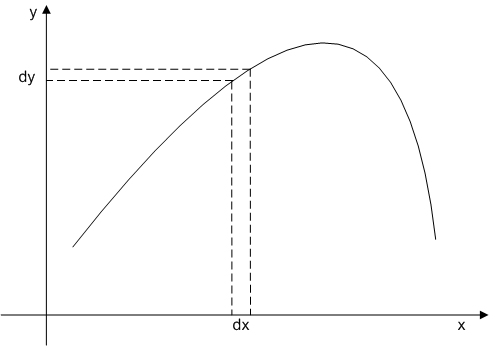
上の図は,微分法の計算をするときのイメージを絵にしてみたものです.図中に曲線として表されている関数 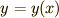 があります.点線で表してあるように,変数
があります.点線で表してあるように,変数  をほんの少し変化させると,それに応じて,関数値
をほんの少し変化させると,それに応じて,関数値 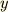 もほんの少しだけ変わっています.曲線の形自体は変わっていません.
もほんの少しだけ変わっています.曲線の形自体は変わっていません.

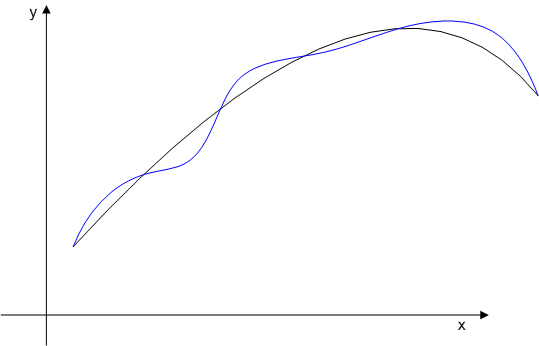
今度は,変分問題のイメージです.変化したのは,変数ではなくて,関数形そのものです.もっとぐにゃぐにゃに変わったっていいのですが,一応,形の変化は連続的で滑らかな変化だということにします.微分法との違いは,はっきり分かったでしょうか.イメージを持つことが大切です.
もっとも,この記事で私達が考える変分法は,汎関数が ![I[y]\equiv \int _{a}^{b}f(x,y,y')dx](./26d978851963de88325d8681d335da87.png) のように,積分の形で表されるものですので,条件はもっと緩いのですが,変分問題とは何かというイメージとしては,上の図のようなものを考えたらいいと思います. [*]
のように,積分の形で表されるものですので,条件はもっと緩いのですが,変分問題とは何かというイメージとしては,上の図のようなものを考えたらいいと思います. [*]
| [*] | 微分が『微小部分の変化率』を意味したのに対し,積分は『全体の合計』を意味しています.例えば,年間の売り上げを計算する場合,微分原理に従うというのは,毎分毎秒の収入と支出を時々刻々計算するようなものです.それに対し,積分原理に従うというのは,一年を通じての全体の収支だけを見るようなものなのです.積分の方が,少し条件が緩そうだということが想像できましたか?どこかで帳尻が合っていれば,少しぐらい途中で何か起こっていても,積分原理では気にしないのですね. |
変分問題を解くには次の二つの方法があります.
- オイラー方程式を解く.
- 直接法で解く.
汎関数が ![I[y]\equiv \int _{a}^{b}f(x,y,y')dx](./26d978851963de88325d8681d335da87.png) のように,関数
のように,関数 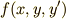 の積分として定義されているとき,オイラー方程式というものを解けば,汎関数に極値を与える
の積分として定義されているとき,オイラー方程式というものを解けば,汎関数に極値を与える 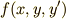 の関数形が求まってしまいます.詳しくは,次のセクションで勉強します.また,関数が
の関数形が求まってしまいます.詳しくは,次のセクションで勉強します.また,関数が 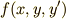 という形でない場合(もっとたくさん変数を含む場合,さらに高次の導関数を含む場合等々)については, 変分法2 で扱います. [†]
という形でない場合(もっとたくさん変数を含む場合,さらに高次の導関数を含む場合等々)については, 変分法2 で扱います. [†]
| [†] | 慣れてしまえば何でもないのですが,最初,汎関数が積分の形で表現されていることに困惑する人が多いようです.変分法を物理で使うとなると,力学の最小作用の原理,光学のスネルの法則などが代表的なものですが,それらの法則を勉強してみると,積分によって物理量が表現されるというのがごく自然なことだということが感じられると思います.今は,ピンと来なくても,そんなもんかな,と思っておいて下さい.前の註にも書いたように,大雑把な言い方ですが,積分方程式の条件は微分方程式の条件よりも緩く,結果オーライなところがあります.式の形はよく分からないけれども,とりあえず結果はこれこれこうあって欲しいな,という場合に,まず積分方程式が出てくるのは,自然な成り行きです. |
オイラー方程式を使う方法は非常に強力なので,変分法の解法といえば,オイラー方程式を解くだけだと思ってしまいがちですが,コンピューターで数値計算する場合に,大体の関数形が分かっているならば,実際に関数形を少しだけいじってみて,汎関数の値の増減を調べるという方法があります.これを 直接法 と呼びます.数値計算を将来専門にする人は,これも頭のどこかに覚えておくといいかも知れません.これについては,この記事では触れません.
オイラー方程式を求める
ここからは数学的に考えます. 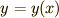 という関数があり,関数
という関数があり,関数 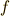 は
は 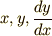 によって決まる関数とします.以後
によって決まる関数とします.以後 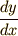 を
を 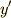 と書きます.この段階では,まだ
と書きます.この段階では,まだ 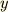 がどんな関数かわかりません..
がどんな関数かわかりません..
この 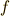 の積分によって汎関数
の積分によって汎関数 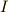 が次のように積分の形で与えられます.(ここがポイント!)
が次のように積分の形で与えられます.(ここがポイント!)
![\displaystyle I[y]\equiv \int _{a}^{b}f(x,y,y')dx \tag{1}](./b539c14a88fdc8cfab99a9ead95078bc.png)
この 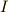 が停留値をもつ(極大か極小か変曲点である)ように関数
が停留値をもつ(極大か極小か変曲点である)ように関数 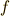 の関数形を求めるというのが変分問題です.基本的な考え方は微分と同じで,停留値の近くでは,関数形を少し変えたときの汎関数の変化
の関数形を求めるというのが変分問題です.基本的な考え方は微分と同じで,停留値の近くでは,関数形を少し変えたときの汎関数の変化 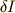 (これを 第一変分 と呼ぶ)が非常に小さいということを利用します.
(これを 第一変分 と呼ぶ)が非常に小さいということを利用します.
関数  が最初
が最初 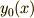 という関数だったとし,これに対して任意の関数
という関数だったとし,これに対して任意の関数 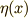 と,ある微小な量
と,ある微小な量  を導入し,次のように
を導入し,次のように  をほんの少しだけ変形させます.(関数の形そのものを変形させるという点が重要です.)積分区間の両端では,変形が無いように,
をほんの少しだけ変形させます.(関数の形そのものを変形させるという点が重要です.)積分区間の両端では,変形が無いように, 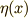 には,式(3)のような境界条件も与えておきます.
には,式(3)のような境界条件も与えておきます.

ここで導入した  は,『関数形を変形させる変数』とでも考えたらいいでしょう.汎関数Iに停留値を与える関数形に対しては,ホンの少し関数形が変化しても汎関数の変化は非常に小さいはずです.(微分の考え方と比べてみてください.関数
は,『関数形を変形させる変数』とでも考えたらいいでしょう.汎関数Iに停留値を与える関数形に対しては,ホンの少し関数形が変化しても汎関数の変化は非常に小さいはずです.(微分の考え方と比べてみてください.関数  変数,関数形
変数,関数形  変数の値,汎関数
変数の値,汎関数  関数,とそれぞれ言い換えれば,やっていることは微分の計算と同じようなものだと分かります.)
関数,とそれぞれ言い換えれば,やっていることは微分の計算と同じようなものだと分かります.)
したがって, 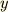 が停留値を与えるという条件は,次が成り立つことだと言えそうです.これは普通の微分です.
が停留値を与えるという条件は,次が成り立つことだと言えそうです.これは普通の微分です.
![\displaystyle {dI[y]\over d\varepsilon }\Big\arrowvert _{\varepsilon =0}=0 \tag{4}](./c521c44ad4df77704de03a5f38c267a8.png)
そこで,式(1)から,汎関数を微分してみます.一気に4行ほど式変形します.式変形の説明は,すぐ下に日本語で書きます.
![\displaystyle {dI\over d\varepsilon }&={d \over d\varepsilon} \int _{a}^{b} f(x,y,y')dx \\ &=\int _{a}^{b}\Big({\partial f\over \partial y}\cdot {\partial y\over \partial \varepsilon }+{\partial f\over \partial y'}\cdot {\partial y'\over \partial \varepsilon }\Big)dx \\&=\int _{a}^{b}\Big({\partial f\over \partial y}\eta (x)+{\partial f\over \partial y'}\eta '(x)\Big)dx \\&=\bigg[{\partial f\over \partial y'}\eta (x)\bigg]_{a}^{b}+\int _{a}^{b}\eta (x)\biggl\{ {\partial f\over \partial y}-{d\over dx}\Big({\partial f\over \partial y'}\Big)\biggr\} dx \tag{5}](./d40a23b500ea12466ac1d8242995c5b8.png)
一行目から二行目では,微分のチェーンルールを使いました.二行目から三行目では,式(2)より 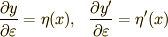 が成り立つことを使っています.そして,三行目から四行目では,右辺の第二項だけを 部分積分 しました.
が成り立つことを使っています.そして,三行目から四行目では,右辺の第二項だけを 部分積分 しました.
さて,部分積分して前に出した項は, 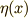 の境界条件である式(3)より零になってしまいますので,結局,積分の部分しか残りません. [‡]
の境界条件である式(3)より零になってしまいますので,結局,積分の部分しか残りません. [‡]
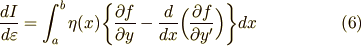
ここで 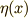 は任意の関数だということでしたから,右辺が恒等的に零になるには,中括弧でくくってある部分が恒等的に零になる他ありません.
は任意の関数だということでしたから,右辺が恒等的に零になるには,中括弧でくくってある部分が恒等的に零になる他ありません.
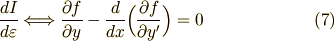
これを オイラー方程式 と呼びます.
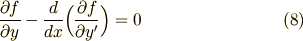
| [‡] | 任意の関数 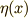 と言っておきながら,なんだか境界条件だけは,課すというのは,すっきりしないと感じた人がいるかも知れません.部分積分の後, 前に出した と言っておきながら,なんだか境界条件だけは,課すというのは,すっきりしないと感じた人がいるかも知れません.部分積分の後, 前に出した 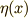 の項が境界条件(3)によってうまく消える仕組みになっていますが,逆に言えば,ここで の項が境界条件(3)によってうまく消える仕組みになっていますが,逆に言えば,ここで 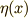 が消えてくれなければ困るので,最初に無理矢理に境界条件をこじつけたというが正直なところです.部分積分で前に出した部分さえ消えてくれれば良いので,境界条件として固定端条件 が消えてくれなければ困るので,最初に無理矢理に境界条件をこじつけたというが正直なところです.部分積分で前に出した部分さえ消えてくれれば良いので,境界条件として固定端条件 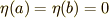 が常に必要なわけではなく,(5)式の最後の行を見れば分かるように, が常に必要なわけではなく,(5)式の最後の行を見れば分かるように, 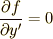 が成り立っている場合には,(3)式の境界条件は必ずしも必要ではないのです.この形の境界条件を 自由端条件 と呼びます.物理の問題に出てくる境界条件の多くは,固定端条件か自由端条件でなんとかなるものが多いので,まずはこの二つを覚えておけば大丈夫です.今は,一気に覚えようとすると混乱すると思いますので,本文に書いた 固定端条件 をしっかりと理解するようにしてください. が成り立っている場合には,(3)式の境界条件は必ずしも必要ではないのです.この形の境界条件を 自由端条件 と呼びます.物理の問題に出てくる境界条件の多くは,固定端条件か自由端条件でなんとかなるものが多いので,まずはこの二つを覚えておけば大丈夫です.今は,一気に覚えようとすると混乱すると思いますので,本文に書いた 固定端条件 をしっかりと理解するようにしてください. |
部分積分が出てきたりして少し面倒だったかも知れませんが,オイラー方程式の導出は大変重要です.一人で導けるようになるまで,何度も練習してみて下さい.この記事では,汎関数を与える関数として, 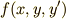 という形のものしか扱いませんでしたが,もっと変数が多い場合や,高階導関数を含むような場合については 変分法2 で,演習問題と併せて触れます.
という形のものしか扱いませんでしたが,もっと変数が多い場合や,高階導関数を含むような場合については 変分法2 で,演習問題と併せて触れます.