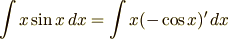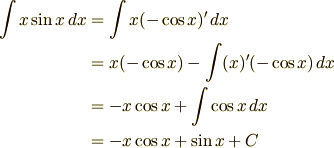部分積分
積分公式を一番よく覚えているのは大学入試直前ではないでしょうか. 大学生以上になると授業での演習量が減るのでどんどん忘れて行きます. 授業の最後にたまに演習問題があることがあるんですが, 部分積分がさっぱり分からなくなっていて問題が解けなかったので復習しました.
部分積分の公式
つぎの積分公式
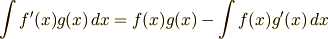
を部分積分といいます.2つの関数のかけ算になっている被積分関数の1つ(この場合は 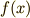 )
だけを部分的に積分するので部分積分といいます.定積分の場合は
)
だけを部分的に積分するので部分積分といいます.定積分の場合は
![\int_a^b f'(x)g(x)\,dx=\left[f(x)g(x)\right]_a^b-\int_a^b f(x)g'(x)\,dx](./7f85bf75ca3331f34449e150a974939c.png)
となります.それぞれの公式の証明は教科書に書いてあると思いますが,部分積分の公式は覚えておくべきです. これだけではよく分からないので例題をみて行きましょう.
例題3. log x の積分
つぎの積分を実行せよ.
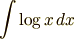
解
これは被積分関数が掛け算になっていません.一見簡単そうにみえますが,
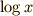 の積分公式はないのですぐには解けません.そこで部分積分の公式をつかうために,
の積分公式はないのですぐには解けません.そこで部分積分の公式をつかうために,
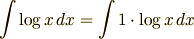
というふうに無理矢理掛け算にしておきます.  で微分して1になるのは
で微分して1になるのは  ですから,
部分積分の公式からつぎのように積分計算ができます.
ですから,
部分積分の公式からつぎのように積分計算ができます.
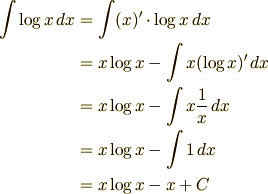
例題4. 少し複雑な積分
1種類の単原子分子からなる気体のマクスウェルの速度分布関数は次式で表される.
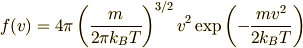
この気体分子の速度の平均値 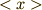 は,速度に上式を掛け,
は,速度に上式を掛け,
 空間で積分することで求められる.
空間で積分することで求められる. 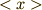 を計算せよ.
を計算せよ.
解
この問題が例の,崎間が授業中解けなかったってやつです(他の人たちは解けてた).まず,問題文の通りにやると
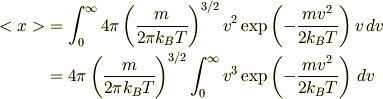
となります.このままではやりにくいので 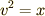 と置いて積分変数を置換します.
と置いて積分変数を置換します.
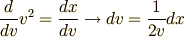
より
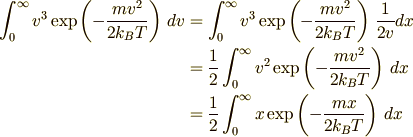
です.ここで部分積分を行います,ってうわーなんだこれは.メゲずに黙々とやりましょう.
![\frac{1}{2}\int_0^{\infty}&x\exp\left(-\frac{mx}{2k_BT}\right)\,dx\\ &= \frac{1}{2}\int_0^{\infty}x\left(-\frac{2k_BT}{m} \exp\left(-\frac{mx}{2k_BT}\right)\right)'\,dx\\ &= \frac{1}{2}\left[x\left(-\frac{2k_BT}{m}\exp\left(-\frac{mx}{2k_BT}\right)\right)\right]_0^{\infty} -\frac{1}{2}\int_0^{\infty}(x)'\left(-\frac{2k_BT}{m}\exp\left(-\frac{mx}{2k_BT}\right)\right)\,dx\\ &= -\frac{k_BT}{m}\left[x\exp\left(-\frac{mx}{2k_BT}\right)\right]_0^{\infty} +\frac{k_BT}{m}\int_0^{\infty}\exp\left(-\frac{mx}{2k_BT}\right)\,dx\\ &= 0+\frac{k_BT}{m}\left[-\frac{2k_BT}{m} \exp\left(-\frac{mx}{2k_BT}\right)\right]_0^{\infty}\\ &= -\frac{2{k_B}^2T^2}{m^2}(0-1)\\ &= \frac{2{k_B}^2T^2}{m^2}](./51bc0fbca29e9fbd47f99c86b0fd8687.png)
なんとかスッキリしました.  になるのはいいですよね.
になるのはいいですよね.
これでやっと,求めるべき平均速度 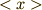 が
が
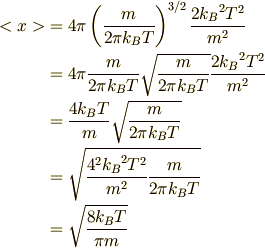
と求まります.やたらと繁雑でしたが,計算間違いをしないようにしましょう (この記事を書くとき僕は何回も計算を間違えてました).
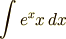
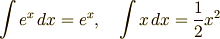
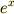 と
と 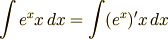
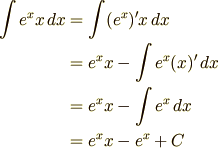
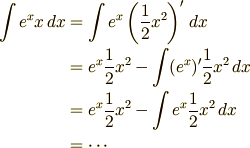
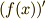 の形にすればいいかは,
何度か部分積分の問題を解いていったら自然に分かると思います
の形にすればいいかは,
何度か部分積分の問題を解いていったら自然に分かると思います 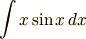
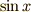 になるのは
になるのは 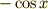 ですから,
ですから,