最速降下曲線
最速降下曲線というのは,曲線に沿って物を転がしたときに,物が一番速く転がり落ちる曲線のことです.このカーブで滑り台を作れば,一番スピードが出るということです.私は小さい頃,ものすごく大きな滑り台を物凄く高いところから滑ったらどんなに気持ち良いだろう,とよく夢想していました.箱根の遊園地に山の斜面を利用した数百メートルという滑り台があるときき,ある日親に連れて行ってもらったのですが,途中に砂利や落ち葉が詰まっていたりして,想像していたものとは程遠いものでした.読者の中から,本稿を読んで,世界最速滑り台を作ってみる人が現れることを切に願います.さて,途中で 変分法1 の知識が必要になります.また サイクロイド振り子 の項も参照してみてください.
歴史的背景
この問題はなかなか由緒正しい問題です.古代ギリシャの数学者や,ガリレオも取り組んだようですが,1696年にスイスの数学者ヨハン・ベルヌーイ(1667-1748)によって提起されたものを嚆矢とすることが多いようです.ベルヌーイ家は元々ベルギー出身ですが,ヨハンの祖父の代に宗教的迫害を逃れてスイスに移住してきました.息子や孫を含めて8人もの高名な数学者・物理学者を輩出している数学一家です.(ベルヌーイ一家の家系図に興味のある方は ここ を参照して下さい.)ヨハンは人間関係で衝突の多かった人のようで,ロピタルの定理に名前の残っているフランスのロピタル公爵や,確率論で有名な兄のヤコブ・ベルヌーイと深刻な論争をしています.(ヨハンが家庭教師をしていたときのノートを,ロピタル公爵が自著として出版してしまった,とヨハンは主張しました.ヤコブとの論争はヤコブが自分より先に大学の教授職に就いたことに対する単なるやっかみだという噂ですが,真相はわかりません.)流体力学で有名な息子のダニエールがパリ科学学会の賞を取ったときには,怒って勘当してしまっています.怒ってしまった理由は不明ですが,とにかく,人との争いが耐えない人だったようです.ニュートンとライプニッツが微積分法のアイデアを巡って大論争を続けていたときには,友人だったライプニッツの側に立って自ら他人の喧嘩に参加したりしています.自分の知り合いにこんな人がいたらさぞ厄介でしょう.
ベルヌーイの話が長くなりました.最速降下曲線問題の話に戻ります.ベルヌーイの提起した問題というのは『決まった二点の間を,始点から終点まで玉が一番速く転がることが出来るような曲線を求める』というものです.もちろん,終点は始点よりもちょっと低くなっていて,少し離れているものとします.公開後しばらくして,ライプニッツの提案により,ベルヌーイはこの問題を海外の数学者にも公開することにしました.もちろんニュートンの鼻を明かしてやるつもりだったのです.ところがこの問題を受け取ったニュートンは大変疲れていたにも関わらず一晩で解いてしまったそうで,ベルヌーイとライプニッツは大変に悔しがりました.ニュートンの日記にはその日のことを次のように記してあります.
... in the midst of the hurry of the great recoinage, did not come home till four (in the afternoon) from the Tower very much tired, but did not sleep till he had solved it, which was by four in the morning. (わしは,王立造幣局の仕事が大忙しで,午後四時までは家にも帰れず,くたくたに疲れていたのじゃが,その問題を解くまでは寝なかったんじゃ.といっても,朝の四時までには解けてしまったんじゃが.(訳注:ニュートンは当時,王立造幣局の監督に任命され,金と銀の価値比率を決める仕事や,贋金犯の処罰に精力的に取り組んでいました.Joh訳)
しかしニュートンも名誉欲や権勢欲の大変強い人で,自分の日記が死後出版されるまで想定していたという話もあるくらいなので,これが本当の話なのか,単なる自慢話なのかは分かりません.結局,ベルヌーイの設定した期限内に回答を寄せてきたのは,ライプニッツ,兄のヤコブ・ベルヌーイ,ニュートン,ロピタルの4人だけでした.1697年に解答が発表されたとき,なぜかロピタルだけは無視され,他の4人の解答が発表されました.ロピタルの証明は1988年になってようやく発見され,正しいことが確認されました.
最速降下曲線を求める
前置きが大変長くなりましたが,計算に入ります. 変分法1 の基礎が分かっていることが前提になっています.またベルトラミの公式を使いますので忘れてしまった人は先に 変分法2 を復習して下さい.
最終的に求めたいのは関数形 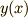 ですが,変分法の問題ではまず,極値もしくは停留値を取る汎関数
ですが,変分法の問題ではまず,極値もしくは停留値を取る汎関数 ![I[y]](./15ed8cca5742103c5bdb7f8e11f0dfb1.png) を,ある量
を,ある量 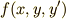 の積分で表現してやります.そして
の積分で表現してやります.そして ![I[y]](./15ed8cca5742103c5bdb7f8e11f0dfb1.png) が極値もしくは停留値を取るここと
が極値もしくは停留値を取るここと 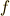 がオイラー方程式を満たすことは同値なので,次にオイラー方程式を解くという段取りで計算が進んで行きます.(
がオイラー方程式を満たすことは同値なので,次にオイラー方程式を解くという段取りで計算が進んで行きます.(  は
は 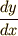 を表しています.)
を表しています.)
![\displaystyle I[y]\equiv \int _{a}^{b}f(x,y,y')dx \tag{1}](./44b644d97432cca65cbbb8316389e44c.png)
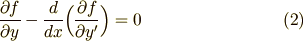
説明の中に 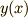 と
と 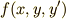 と
と ![I[y]](./15ed8cca5742103c5bdb7f8e11f0dfb1.png) が一度に出てくるので,慣れていないと何を言っているのかちょっと混乱しそうですね.変分法の問題は,式(1)のような汎関数をうまく表現するということと,(2)オイラー方程式を解く,という二段階構造になっていると思ってください.
が一度に出てくるので,慣れていないと何を言っているのかちょっと混乱しそうですね.変分法の問題は,式(1)のような汎関数をうまく表現するということと,(2)オイラー方程式を解く,という二段階構造になっていると思ってください.
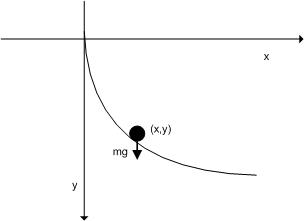
具体的にこの問題では,求めたい曲線の関数形を 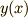 とします.座標は次の図のように
とします.座標は次の図のように 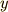 軸を下向きに取って
軸を下向きに取って 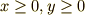 の範囲を考えます.この段階では図に描いてある曲線はいい加減なものだということに注意して下さい.いま何を最小値にしたいかと言えば時間ですから,式(1)の
の範囲を考えます.この段階では図に描いてある曲線はいい加減なものだということに注意して下さい.いま何を最小値にしたいかと言えば時間ですから,式(1)の ![I[y]](./15ed8cca5742103c5bdb7f8e11f0dfb1.png) としては時間
としては時間 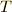 を置きます.そして,時間を上手く式(1)の形で表現する
を置きます.そして,時間を上手く式(1)の形で表現する 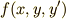 を求めます.この
を求めます.この 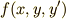 も今の段階ではどんな形なのかは見当もつきません.とりあえず,玉が転がるのにかかる時間を,曲線の関数形で表現するところから始めましょう.
も今の段階ではどんな形なのかは見当もつきません.とりあえず,玉が転がるのにかかる時間を,曲線の関数形で表現するところから始めましょう.
汎関数をうまく表現する
玉が転がるのにかかる時間 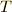 を積分の形で表すことから始めます.玉の速度は一定ではありませんので,次のような,瞬間瞬間の速度の積分として表現されるはずです.添字の
を積分の形で表すことから始めます.玉の速度は一定ではありませんので,次のような,瞬間瞬間の速度の積分として表現されるはずです.添字の  ,
,  は,スタート地点と到達地点をそれぞれ表しています.
は,スタート地点と到達地点をそれぞれ表しています.

この 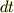 を上手く
を上手く  ,
, 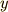 ,
, 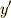 で表したいですね.すこしそのための道具を揃えましょう.曲線の微小要素を
で表したいですね.すこしそのための道具を揃えましょう.曲線の微小要素を 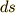 とするとき,ピタゴラスの定理から次の関係が成り立ちます.
とするとき,ピタゴラスの定理から次の関係が成り立ちます.
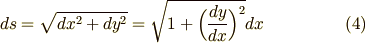
それから,玉の速度  は曲線の上で距離を時間で微分すればいいのですから,次のように書けます.
は曲線の上で距離を時間で微分すればいいのですから,次のように書けます.
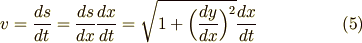
なんだか 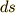 とか
とか 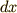 とかがたくさん出てきましたが,式(3)の右辺の
とかがたくさん出てきましたが,式(3)の右辺の 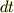 を
を 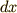 に変換したいので,チェーンルールで変数変換することを目論んでいたのです.式(4)(5)を使うと,式(3)は次のように書き換えられます.
に変換したいので,チェーンルールで変数変換することを目論んでいたのです.式(4)(5)を使うと,式(3)は次のように書き換えられます.
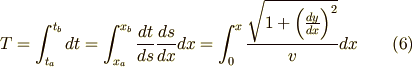
だんだん右辺がそれらしくなってきました.ところで玉には重力以外の外力はかかっていないので,落ちた距離 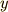 と速度
と速度  の間にはエネルギー保存則
の間にはエネルギー保存則 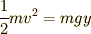 が成り立つはずです.(ようやく物理が出てきました!!)これを変形して,
が成り立つはずです.(ようやく物理が出てきました!!)これを変形して, 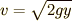 と書けます.これを式(6)に代入すれば次のようになります.
と書けます.これを式(6)に代入すれば次のようになります.
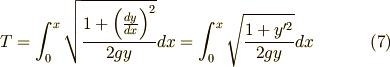
積分の中身は 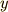 と
と 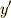 だけの関数になっていますから,見事に汎関数を表現することが出来ました.式(1)と見比べてみれば,この問題では
だけの関数になっていますから,見事に汎関数を表現することが出来ました.式(1)と見比べてみれば,この問題では 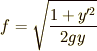 となっていることが分かります.
となっていることが分かります.
オイラー方程式を解く
この問題の汎関数が式(7)のように求まったので,次にいよいよオイラー方程式を解きます. 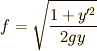 をオイラー方程式
をオイラー方程式 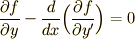 に代入すれば良いのです.ここからは一本道ですから,このままぐいぐいと計算を進めても問題はありませんが,よく見ると
に代入すれば良いのです.ここからは一本道ですから,このままぐいぐいと計算を進めても問題はありませんが,よく見ると 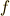 には
には  が陽に含まれていません.つまり
が陽に含まれていません.つまり 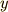 と
と 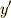 だけの関数になっています.これはオイラー方程式の代わりにベルトラミの公式が使える形でした.こういう場合にはベルトラミの公式(式(8))から出発した方が,後で計算がずっと楽になります.(これはオイラー方程式の特別な場合に過ぎません.ここから先の計算を(2)式のオイラー方程式から初めても,途中の計算が面倒臭いだけで同じ結果を得られます.詳しくは 変分法2 を参照して下さい.)式中,
だけの関数になっています.これはオイラー方程式の代わりにベルトラミの公式が使える形でした.こういう場合にはベルトラミの公式(式(8))から出発した方が,後で計算がずっと楽になります.(これはオイラー方程式の特別な場合に過ぎません.ここから先の計算を(2)式のオイラー方程式から初めても,途中の計算が面倒臭いだけで同じ結果を得られます.詳しくは 変分法2 を参照して下さい.)式中, 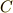 は定数です.
は定数です.

ここに先ほどの 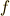 を代入します.
を代入します.
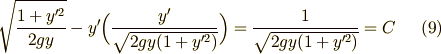
両辺を二乗すると次の形に整理できます.右辺は定数なので, 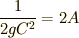 と置き直しました.
と置き直しました.
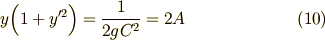
式(10)を次のように変形します.

いま,曲線の定義域としては 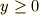 を考えています.また
を考えています.また 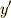 は実数でないと困りますので,これより
は実数でないと困りますので,これより 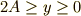 という条件が必要です.もう一つ,初期条件として
という条件が必要です.もう一つ,初期条件として 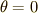 のとき,
のとき, 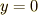 という条件も必要です.このとき
という条件も必要です.このとき 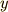 を次のようにパラメーター表示することができます.まずは
を次のようにパラメーター表示することができます.まずは 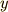 をパラメーター表示してしまって,
をパラメーター表示してしまって,  は後からうまく決めようという方針で行きます.
は後からうまく決めようという方針で行きます.

また,式(12)を両辺微分すれば次のようになります.これはちょっと後で使います.
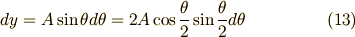
さて,この 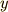 のパラメーター表示を使うと,式(11)は次のように書き直すことが出来ます.
のパラメーター表示を使うと,式(11)は次のように書き直すことが出来ます.
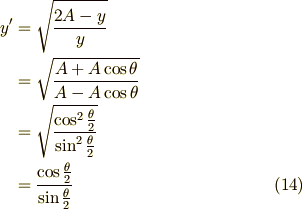
両辺に 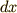 を掛けて,次のように書いておきます.
を掛けて,次のように書いておきます.

方針が見えてきましたでしょうか?式(13)と式(15)を連立して, 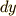 を消去すれば
を消去すれば  と
と 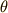 の関係式を求めることが出来るわけです.
の関係式を求めることが出来るわけです.
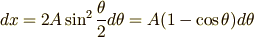
両辺積分を積分して,  のパラメーター表示も無事に出てきました.
のパラメーター表示も無事に出てきました.
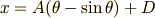
ここで 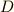 は積分定数ですが,いま初期条件として
は積分定数ですが,いま初期条件として 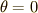 のとき
のとき 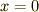 を考えていますので,
を考えていますので, 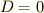 が決まります.結局,最速降下曲線の方程式はパラメーター表示で次のように求まりました.
が決まります.結局,最速降下曲線の方程式はパラメーター表示で次のように求まりました.


この表式を見て,曲線の様子が想像できますか?実は,この  ,
, 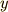 によって表されるのは,次のようなサイクロイドとなります.
によって表されるのは,次のようなサイクロイドとなります.
以上で,最速降下曲線はサイクロイドだということが分かりました.
最速降下曲線の例
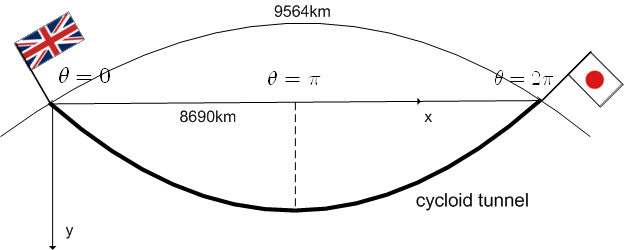
例として,ロンドンと東京を最速降下曲線でできたトンネルでつなげたらどれくらいで行き来できるようになるか計算してみましょう.トンネル中の空気抵抗や摩擦抵抗は考えないことにします.
地球を平らだと見なすのは幾らなんでもあんまりなので,地面の中を結んだ直線距離を求めましょう.ロンドンと東京の距離は地表で ![9564 {\rm [km]}](./c3cfcfae9c21f0e5d8b3dec75b3c6141.png) だということですので,直線で結ぶと約
だということですので,直線で結ぶと約 ![8690 {\rm [km]}](./c85c9e69bd748ff4a255ea3c60bfa3f4.png) になります.(地球を円周
になります.(地球を円周 ![40000 {\rm [km]}](./611665217964c193afb14a6123783559.png) の球として計算しました.)
の球として計算しました.)
式(7)から時間 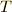 を求めます.ここで
を求めます.ここで 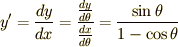 に注意してください.
に注意してください.
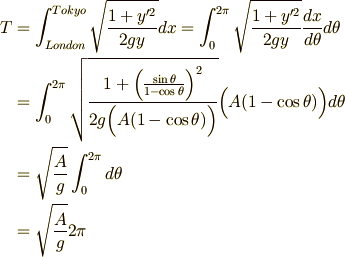
図を見れば 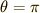 のとき
のとき ![x= 2A \pi =8690 {\rm [km]}](./9be8727a2b893d3cd4a3107c2ada5278.png) ですので,ここではおおよそ
ですので,ここではおおよそ ![A=1383.576 {\rm [km]}](./584a4513bcd4a00048c06e93c6d803ed.png) とわかります.
とわかります. ![g=9.8 {\rm [m/s^2]}](./4c0a380b282622db34ace5125bc09696.png) として,約
として,約 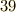 分という結果を得ます.トンネルを掘っておいてロンドンで何か落とせば,エンジンとか何にもなくても
分という結果を得ます.トンネルを掘っておいてロンドンで何か落とせば,エンジンとか何にもなくても 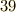 分後には東京に着いているということです.早すぎます!!
分後には東京に着いているということです.早すぎます!!
等時性について
補足ですが,このサイクロイドトンネルには,斜面のどこから玉を転がしても,最下点に到達するまでにかかる時間が同じだという特徴があります.上の例で言えば,トンネル内のどこか途中から玉を転がし始めても,ちょうど反対側まで行くのには 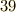 分かかるということです.何だか少し不思議な感じのする話です.これについては サイクロイド振り子 のページに少し説明がありますので,そちらも是非読んでみてください.
分かかるということです.何だか少し不思議な感じのする話です.これについては サイクロイド振り子 のページに少し説明がありますので,そちらも是非読んでみてください.
英語で何というか
より詳しく洋書や海外のサイトで勉強する人のために,キーワードを英語で何というか紹介しておきます.最速降下曲線問題は 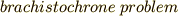 といいます.この
といいます.この 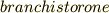 というのはギリシャ語で「最短時間」を意味する言葉で,ヨハン・ベルヌーイによって作られた単語です.他で使っているのを見たことはありません.変分法は
というのはギリシャ語で「最短時間」を意味する言葉で,ヨハン・ベルヌーイによって作られた単語です.他で使っているのを見たことはありません.変分法は 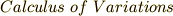 といいます.なぜか日本語には変分法の詳しい教科書があまりありません.意欲のある人は英語の教科書で勉強するのが一番良さそうです.ヨハン・ベルヌーイの名前は英語風に
といいます.なぜか日本語には変分法の詳しい教科書があまりありません.意欲のある人は英語の教科書で勉強するのが一番良さそうです.ヨハン・ベルヌーイの名前は英語風に 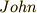 ,ドイツ語で
,ドイツ語で  もしくは
もしくは  ,フランス語で
,フランス語で  などと,色々に書かれることがありますが,どれも同じです.息子や孫にもヨハンというのがいるので,区別のためにI(一世)がつくこともあります.苗字の綴りは
などと,色々に書かれることがありますが,どれも同じです.息子や孫にもヨハンというのがいるので,区別のためにI(一世)がつくこともあります.苗字の綴りは  です.
です.