サイクロイド振り子
ここではサイクロイド振り子について紹介します. サイクロイド振り子がどのような特徴を持つのか,その周期はどのような形で表されるのかについて解説します. そして,類似の物理をもつサイクロイド軌道上の運動についても触れます.
サイクロイド振り子とは
図のように,二つのサイクロイドのあいだに挟まれた振り子を考えます.
サイクロイドを描いた円の半径を  とするとき,振り子のヒモの長さを
とするとき,振り子のヒモの長さを 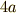 にとると,振り子自身が描く軌跡もサイクロイドになります.
図でいうと青い線が振り子の軌道です.
にとると,振り子自身が描く軌跡もサイクロイドになります.
図でいうと青い線が振り子の軌道です.
このとき,この振り子をサイクロイド振り子と呼びます.
この振り子を研究した研究者の名前をとって,「ホイヘンス振り子」と呼ばれることもあります.
サイクロイド振り子の等時性
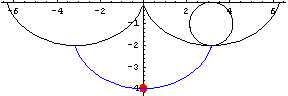
単振り子の場合には,その周期は 楕円積分 で表されました.つまり振幅が大きくなった場合に単振り子の周期は,次式のように振幅 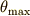 に依存し,一定ではなくなるということでした.
に依存し,一定ではなくなるということでした.
![T(\theta_{\text{max}}) = 2\pi \sqrt {l\over g} \ \Bigl\{ \sum \limits _{n=0}^{\infty }\Big[{(2n-1)!!\over (2n)!!}\Big]^{2}\sin ^{2n}{\theta _\mathrm{max}\over 2}\Bigr\}](./653e6db254714a9ea8c8b597c415091b.png)
振り子を時計代わりに使う場合,徐々に振幅は減衰していきますので,単振り子の場合のようにその周期が振幅に依存しては困ります. サイクロイド振り子はこの点で優れています.振り子の周期が振幅に依らないのです.
実際に触れる様子はつぎの Java Applet のようになります. サイクロイド振り子の周期はその振幅によらないことが確認できるでしょう.
サイクロイド振り子の周期
本当にサイクロイド振り子の周期は振幅に依らないのか,その周期の値はいくらなのかを求めてみましょう.
解析力学を使う
ここでは解析力学から得られる結果を使います. その方が計算が簡単になるのと,周期が振幅によらないことが明確に示せるからです. 力学から周期を求めることも可能で,あとで示します.
まず,系のラグランジアンを求めます.ここではラグランジアン 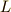 というのは運動エネルギー
というのは運動エネルギー  からポテンシャルエネルギー
からポテンシャルエネルギー 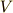 を引いたものだと考えておいてください.
を引いたものだと考えておいてください.
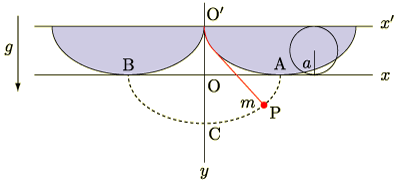
上図の振り子がとるサイクロイド軌道は, サイクロイド の(1),(2)式から
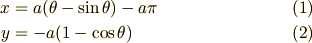
と表されます.ただし 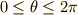 です. [*]
です. [*]
| [*] | 上の図に合わせるために,  軸対称に反転し, 軸対称に反転し,  軸方向に 軸方向に 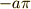 だけ平行移動しました. だけ平行移動しました. |
それぞれを時間微分すると

となります.
運動エネルギー 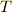 は (3),(4)式より
は (3),(4)式より
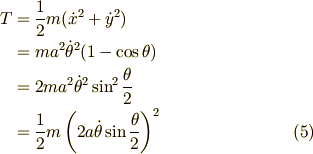
です.2行目から3行目の変形には三角関数の半角の公式 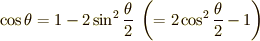 を用いました.
を用いました.
ポテンシャルエネルギー 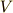 は
は
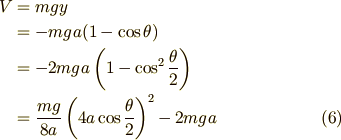
となります.ここでも先ほど用いた半角の公式を使用しました.
ここで 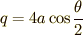 という変数変換をします.
すると
という変数変換をします.
すると 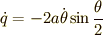 ですから,ラグランジアン
ですから,ラグランジアン 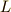 は次のように書けます.
は次のように書けます.
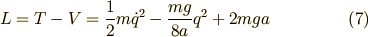
これより,オイラー・ラグランジュの方程式から,ニュートンの運動方程式を計算すると
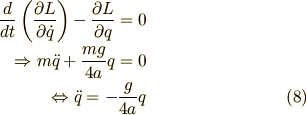
となります.(8)式は 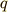 に関する単振動の方程式です.つまり,系は周期
に関する単振動の方程式です.つまり,系は周期
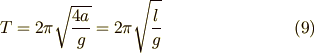
の運動をすることになります.
ここでサイクロイド振り子のヒモの長さ 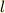 が
が 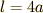 であることを使いました.
であることを使いました.
注意してほしいのは (9)式に初期位置に関する情報が含まれていないことです. つまりこの結果はサイクロイド振り子の周期が振幅によらないということを表しています.
力学から計算する
解析力学からの周期の求め方は,なんだか狐につままれたような気分になるかもしれません. なので,道筋としてはいたってシンプルな力学からの計算法も示しておきましょう.
まずエネルギー保存則を考えます.
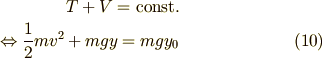
ここで 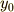 は振り子の初期位置の
は振り子の初期位置の 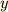 座標です.
座標です. 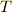 ,
, 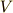 は解析力学の項で考えたものと同じですので,
は解析力学の項で考えたものと同じですので,
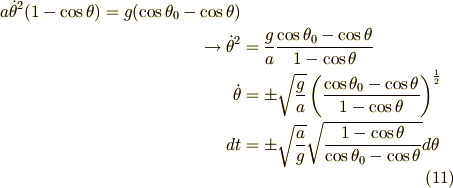
となります.これを積分すれば1周期にかかる時間が求まります.
楕円積分 のところでもやったように, 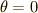 から
から 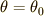 までにかかる時間は1周期の
までにかかる時間は1周期の 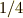 であることが直感的にわかります.
したがって,周期
であることが直感的にわかります.
したがって,周期 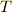 は (11) 式より次のように書かれます.
は (11) 式より次のように書かれます.
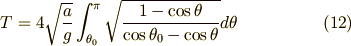
ここで三角関数の半角の公式, 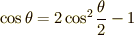 と
と
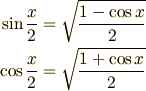
を用いて (12)式を整理すると
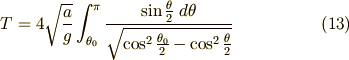
となります.
ここで変数変換 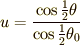 を施すと,
を施すと,
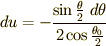 となるので(13)式は
となるので(13)式は
![T & = - 8 \sqrt{ \frac{a}{g}} \int_1^0 \frac{du}{\sqrt{1-u^2}}\\ & = 8 \sqrt{ \frac{a}{g}} \left[ \arcsin u \right]_0^1\\ & = 4 \pi \sqrt{ \frac{a}{g}}\\ & = 2 \pi \sqrt{ \frac{l}{g}} \tag{14}](./3d547f6bc37d4da9703080bc0402274c.png)
となります.これは 解析力学から求めた値 (9)式と一致しています.
(14)式は 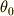 に依らないので,やはり振幅に依存しないことが分かります.
に依らないので,やはり振幅に依存しないことが分かります.
サイクロイド軌道
サイクロイド振り子に似た物理をもつものに一定重力下でのサイクロイド軌道があります. サイクロイド軌道をつくるとどのような特徴が現れるかを見てみましょう.
等時性ふたたび
一定の重力が働く環境でサイクロイド軌道をつくります.その軌道上の異なる高さから,二つの小球を静かに同時に離すとどうなるでしょうか. 次の Java Applet のように,かならず最下点でぶつかることになります.
その理由を考えてみましょう.サイクロイド振り子も,サイクロイド軌道上の運動も,同じ軌道に同じ力で束縛されているという点では一緒です.
「サイクロイド振り子の周期」の解析力学のところの計算は,じつは振り子でなくとも,一定重力下でサイクロイド軌道に沿って運動するのであれば成り立ちます. したがってサイクロイド軌道でもサイクロイド振り子と同じ結論「周期は振幅によらない」がわかります.