楕円積分 〜 振り子の周期を求める
最初に楕円の周の長さを求めてみます.すると楕円積分というものが出てくるので,楕円積分について少し勉強します.最後に,楕円積分のもう一つの例として,有限振幅の単振子の周期を求める計算をします.これが本稿の目標です.途中で テイラー展開 の知識が必要になります.楕円積分とは何なのかを全く知らない人は「はじめに」を読んで下さい.
はじめに
物理の計算をしていて,楕円積分というものに出くわしたことはないでしょうか?例えば,有限振幅の振り子の周期を求める計算や,コマの運動を考えるときに楕円積分という計算が出てきます.普通の教科書では,楕円積分が出てきた時点で「これは楕円積分と言われる計算で初等的には解けない.」と書いてあって,そこで計算が終わっているものがたくさんあります.私はそういうとき,難しくてもいいから最後まで計算が見たい,と思ったものです.きっと他にも最後まで計算の続きが見たい人もいると思い,ここで楕円積分の計算を紹介することにしました.
楕円積分からは楕円関数という関数が定義されます.この分野が難しいと思われているのは,一つには楕円関数の性質が複雑で,計算も面倒だということが言えるでしょう.楕円関数は周期関数なので周期性のある現象を記述するのに適しているのですが,三角関数よりも複雑な二重周期性というものを持っています.そして楕円関数を勉強するには複素関数論が必要になります.物理の計算で少し使いたいだけでも,ここで挫折してしまう人が多いのではないかと思います.楕円関数論というような題名の本を見てみると,大抵は難しい数学ばかりが書いてあって,一筋縄ではいきません.(有名なフェルマーの定理の証明や,最新の暗号理論などにも関係してくるようなので,これはこれで面白そうです.しかしこちらは純粋に数学の世界の話です.)
本稿の立場は,数学的な説明をほとんど無視して,とにかく「有限振幅の振り子の周期を計算してみよう」ということに最終目標を置き,最低限の楕円積分の計算を紹介することだけです.それでも計算はそんなに楽ではありませんが,数学的な内容を思い切って省略すれば,なんとか振り子の周期を求めるところまでは行かれると思います.今後きちんと楕円積分や楕円関数を勉強する第一歩になればと思います.(もっと楕円関数を知りたいという声が多ければ,続編も書きます.)
楕円の周の長さを求める
まず 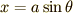 ,
,  で表される楕円の周の長さを求めてみましょう.
で表される楕円の周の長さを求めてみましょう.
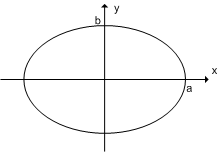
計算は第一象限の弧だけを求めて4倍することにします.
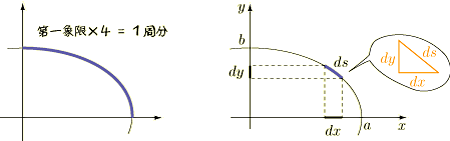
曲線の微小要素の長さ  は,ピタゴラスの定理を使って次のように表せるというのは大丈夫ですね.
は,ピタゴラスの定理を使って次のように表せるというのは大丈夫ですね.
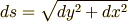
弧の長さはこれを全体に渡って積分すれば求められるはずです. 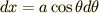 ,
, 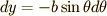 に注意してください.
に注意してください.
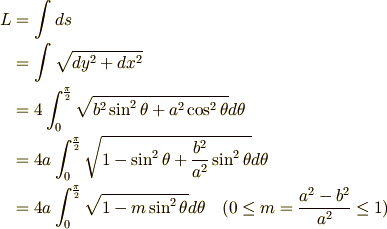
最後の行で 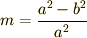 と置きました.(※今,図のように
と置きました.(※今,図のように 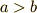 と仮定していますが,もし
と仮定していますが,もし 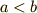 ならば
ならば  と置けば同じ議論が出来ます.)ここまでは,特に難しいことはなかったと思います.さて,この積分をどうやるかが問題です.三角関数が根号の中に入っています.一見,そんなに難しくはなさそうなんですが,やってみるとどうしても積分できません.
と置けば同じ議論が出来ます.)ここまでは,特に難しいことはなかったと思います.さて,この積分をどうやるかが問題です.三角関数が根号の中に入っています.一見,そんなに難しくはなさそうなんですが,やってみるとどうしても積分できません.
そこで,解析的な積分はあきらめて,級数展開してしまいましょう.よく分からない人は,先に テイラー展開 のページを復習してください.(式の中に出てくる!!という記号は『一つおきに階乗を取る』という意味です.例えば 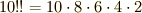 こんな具合です.覚えておくと便利です.)
こんな具合です.覚えておくと便利です.)
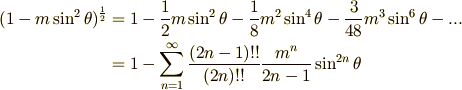
この級数は 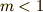 の範囲で一様収束しますので(証明は省きます),和と積分の順序を変えることが許されます.ですから,この級数を使って次のように変形できます.
の範囲で一様収束しますので(証明は省きます),和と積分の順序を変えることが許されます.ですから,この級数を使って次のように変形できます.
![\displaystyle L &=4a\int _{0}^{\pi \over 2}\sqrt {1-m\sin ^{2}\theta }d\theta \\&= 4a\int _{0}^{\pi \over 2}\Bigl\{1-\sum _{n=1}^{\infty }{(2n-1)!!\over (2n)!!}{m^{n} \over 2n-1}\sin ^{2n}\theta d\theta \Bigr\} \\&= 4a\int _{0}^{\pi \over 2}d\theta-\sum _{n=1}^{\infty }{(2n-1)!!\over (2n)!!}{m^{n}\over 2n-1}4a\int _{0}^{\pi \over 2}\sin ^{2n}\theta d\theta \\&= {2a\pi}\Bigl\{ 1-\sum \limits _{n=1}^{\infty }\Big[{(2n-1)!!\over (2n)!!}\Big]^{2}{m^{n}\over 2n-1}\Bigr\}](./4c7dab18b87fa300090cfd0a56cdd76b.png)
最後の行の 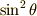 の積分では次の公式を使ってしまいました.話がそれてしまうので,今回はこの公式の証明は省きます.
の積分では次の公式を使ってしまいました.話がそれてしまうので,今回はこの公式の証明は省きます.
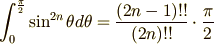
随分と駆け足でしたが,楕円の周の長さを級数表示することができました..ふぅ(汗). 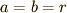 とすると,円周の長さの式
とすると,円周の長さの式 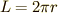 にちゃんと帰着することを確かめて下さい.
にちゃんと帰着することを確かめて下さい.
楕円積分
楕円の周を求める過程で,厄介な積分が出てきました.実は,さっき出てきた積分は『第二標準形の完全楕円積分』と呼ばれる積分なのです.この積分を関数 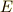 と名付けます.もうみなさんは,第二標準形の完全楕円積分を級数展開で表すとどうなるか知っています.
と名付けます.もうみなさんは,第二標準形の完全楕円積分を級数展開で表すとどうなるか知っています.
![E(m)&=\int _{0}^{\pi \over 2}\displaystyle \sqrt {1-m\sin ^{2}\theta }d\theta \\&= {\pi \over 2}\Bigl\{ 1-\sum \limits _{n=1}^{\infty }\Big[{(2n-1)!!\over (2n)!!}\Big]^{2}{m^{n}\over 2n-1}\Bigr\}](./71fd51c848046b7f96433191243e1285.png)
楕円積分にはこの他に第一標準形と第三標準形というものがあります.これから振り子の周期を求めるのに使うのは,第一標準形の完全楕円積分です.第一標準形の完全楕円積分は次のように表わされる積分で,通例 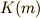 のように書かれます.
のように書かれます.
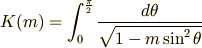
この積分も普通には解けないので,さきほどと同じように級数展開してしまいます.
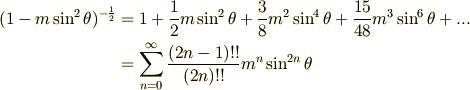
この級数もやはり  の範囲で一様収束するので,次のようにシグマの中を項別に積分することができます.
の範囲で一様収束するので,次のようにシグマの中を項別に積分することができます.
![\displaystyle \int _{0}^{\pi \over 2}\displaystyle (1-m\sin ^{2}\theta )^{-{1\over 2}}d\theta &=\int _{0}^{\pi \over 2}\sum _{n=0}^{\infty }{(2n-1)!!\over (2n)!!}m^{n}\sin ^{2n}\theta d\theta \\&=\sum _{n=0}^{\infty }{(2n-1)!!\over (2n)!!}m^{n}\int _{0}^{\pi \over 2}\sin ^{2n}\theta d\theta \\&={\pi \over 2}\Bigl\{ \sum \limits _{n=0}^{\infty }\Big[{(2n-1)!!\over (2n)!!}\Big]^{2}m^{n}\Bigr\}](./83bf1c7400eebbf00a3f370576317ab8.png)
最後の  の積分では,ふたたび先ほどの公式を使いました.これで,第一標準形の楕円積分も級数表示することができました.
の積分では,ふたたび先ほどの公式を使いました.これで,第一標準形の楕円積分も級数表示することができました.
ここで出てきた 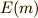 や
や 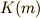 から楕円関数というものが定義されます.前書きで触れたように,そちらの世界に足を踏み入れると大変ですので,今日のところは「難しい積分を無理やり級数展開して,わざわざ名前をつけた」と思っておいて下さい.
から楕円関数というものが定義されます.前書きで触れたように,そちらの世界に足を踏み入れると大変ですので,今日のところは「難しい積分を無理やり級数展開して,わざわざ名前をつけた」と思っておいて下さい.
単振子の周期を求めてみる
振幅が微小な場合(つまり図の 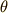 が十分小さい)には,
が十分小さい)には, 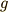 を重力加速度,
を重力加速度, 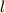 を紐の長さとして,単振子の周期
を紐の長さとして,単振子の周期 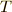 は次の式で表されます.これは本稿では詳しく解説しません.
は次の式で表されます.これは本稿では詳しく解説しません.

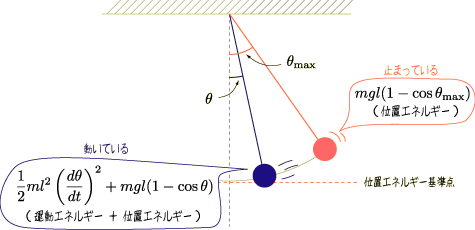
ここからは近似を一切使わず,振幅が小さくない場合を考えます.系のエネルギーとして振り子の運動エネルギーと位置エネルギーの和を考え,エネルギー保存則を議論の出発点にします.

振り子の持つ位置エネルギーは,振り子の一番下から測ることにしましょう.図より,振り子の位置エネルギーは  だということがわかりますね.
だということがわかりますね.
一方,振り子の運動エネルギーは,回転運動であることに注意して,角速度を 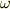 と書けば,
と書けば,
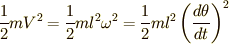 と書けます.
と書けます. 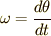 となるのは大丈夫でしょうか.
となるのは大丈夫でしょうか.
さて,振り子が一番大きく振れたときは振り子の速度は零になるので,振り子の持つエネルギーは位置エネルギー  だけになります.その他の角度にあるときの振り子のエネルギーは,位置エネルギーと運動エネルギーの和
だけになります.その他の角度にあるときの振り子のエネルギーは,位置エネルギーと運動エネルギーの和 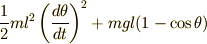 になります.
になります.
この両者が等しいはずなので次の式が成り立ちます.(  は両辺から引いてしまってあります.)
は両辺から引いてしまってあります.)
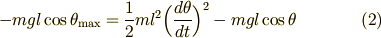
これを  について解くと次のようになります.
について解くと次のようになります.

これは 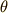 に関する非線形微分方程式ですが,よく見ると変数分離形です.ですから,とりあえず
に関する非線形微分方程式ですが,よく見ると変数分離形です.ですから,とりあえず 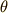 に関する積分と
に関する積分と  に関する積分とに分け,積分します.積分区間なんですが,
に関する積分とに分け,積分します.積分区間なんですが, 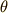 が
が 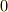 から
から 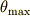 まで振れるのに要する時間は,四分の一周期だということが直感的に分かるので,次のように書いてしまうことにします.
まで振れるのに要する時間は,四分の一周期だということが直感的に分かるので,次のように書いてしまうことにします.
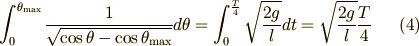
左辺の積分さえうまく求められれば 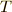 が求められるわけです.ちょっと楕円積分に似ている形ですね.実は,これは第一標準形の完全楕円積分なんですが,分かりやすい形にするために,次のように変数
が求められるわけです.ちょっと楕円積分に似ている形ですね.実は,これは第一標準形の完全楕円積分なんですが,分かりやすい形にするために,次のように変数 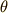 を
を 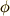 に変数変換してしまいます.こんな変数変換をどうして思いついたんだ!という気がしている読者の方が多いと思います.私もよくわかりませんが,こうすると上手く行くのです.昔の偉い人が思いついてくれたのです.
に変数変換してしまいます.こんな変数変換をどうして思いついたんだ!という気がしている読者の方が多いと思います.私もよくわかりませんが,こうすると上手く行くのです.昔の偉い人が思いついてくれたのです.
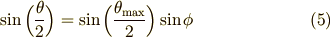
こうすると,(4)式の分母の中は次のようになります.三角関数の半角の公式を使っています.
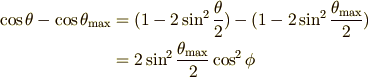
また 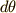 は(5)式の両辺を微分すれば次のようになります.
は(5)式の両辺を微分すれば次のようになります.
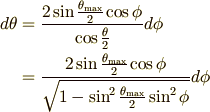
これらを用いて,(4)式を次のように変形します.
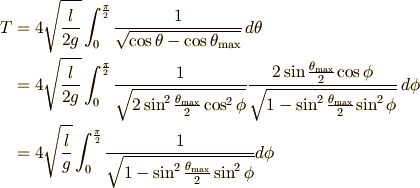
これはどこかで見た形ですね.そうです,第一標準形の楕円積分です.前節で求めた結果を使って一気に最後まで計算してしまいましょう.
![T&=4\sqrt {l\over g}\int _{0}^{\pi \over 2}{1\over \sqrt {1-\sin ^{2}{\theta _\mathrm{max}\over 2}\sin ^{2}\phi }}d\phi \\&=4\sqrt {l\over g}K(\sin ^{2}{\theta _\mathrm{max}\over 2}) \\&=2\pi \sqrt {l\over g}\Bigl\{ \sum \limits _{n=0}^{\infty }\Big[{(2n-1)!!\over (2n)!!}\Big]^{2}\sin ^{2n}{\theta _\mathrm{max}\over 2}\Bigr\} \tag{6}](./739fd7964575bc3e0bcee4963403d529.png)
かくして,振幅が微小ではない場合の振り子の周期が求まりました. 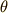 を十分に小さいと近似すると(1)式に帰着することを確認してみて下さい.
を十分に小さいと近似すると(1)式に帰着することを確認してみて下さい.
誤差を考えてみよう
(1)式と(6)式で実際にどれくらいの違いが出てくるのか,大雑把に計算してみることにします.(6)式の級数を次のように最初の三項だけ取ります.これも近似は近似ですが,  の関係する項を全部無視してしまうよりかは,だいぶましなはずです.
の関係する項を全部無視してしまうよりかは,だいぶましなはずです.
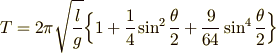
この表式による周期が,(1)式の周期より3%程度大きくなるのは,何度くらいかを求めてみましょう.
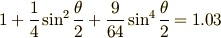
と置くと,これは  に関する二次方程式ですから普通に解けて,
に関する二次方程式ですから普通に解けて, 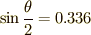 という値を得ます.手元の三角関数表によると,
という値を得ます.手元の三角関数表によると, 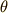 は約38度くらいと求められます.意外と大きな角度なので,
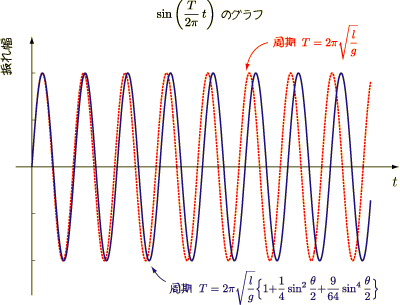
は約38度くらいと求められます.意外と大きな角度なので,  が小さい分には(1)式の精度もひどく悪くはなさそうに思えるかも知れません.しかし一周期分振れる毎に3%の誤差で出るというのは振り子にとっては大きな誤差です.10周期振れたら,30%の誤差が出てくるのです.次の図は振り子にとって3%の誤差がどれくらい大きくなっていくかを示したものです.何周期か振れただけで,目に見えるくらいのずれになっています.楕円積分を求めた甲斐がありました.
が小さい分には(1)式の精度もひどく悪くはなさそうに思えるかも知れません.しかし一周期分振れる毎に3%の誤差で出るというのは振り子にとっては大きな誤差です.10周期振れたら,30%の誤差が出てくるのです.次の図は振り子にとって3%の誤差がどれくらい大きくなっていくかを示したものです.何周期か振れただけで,目に見えるくらいのずれになっています.楕円積分を求めた甲斐がありました.
実際に,どのようにずれるかを視覚的に表したのが次の Java Applet です.左側の青い玉は  の近似を行う前のもの.
右側の赤い玉は
の近似を行う前のもの.
右側の赤い玉は  の近似を行ったものです [1] .小さい角度で振らせていると大した差は出ませんが,大きな角度で振らせているとだんだんズレが大きくなっていくのが確認できます.
の近似を行ったものです [1] .小さい角度で振らせていると大した差は出ませんが,大きな角度で振らせているとだんだんズレが大きくなっていくのが確認できます.
| [1] | 左側の玉はルンゲクッタ法を用いてシミュレーションしています. |
また,振れ角が異なるときの様子を確かめるために次の Java Applet も用意しました.こちらは両方とも 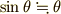 の近似を適用していません [2] .
つまりその周期は楕円積分で表されます.
の近似を適用していません [2] .
つまりその周期は楕円積分で表されます.
| [2] | 両方の玉ともルンゲクッタ法を用いてシミュレーションしています. |