線形微分方程式
つぎの形の微分方程式を線形微分方程式という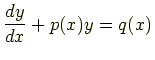 |
(6.10) |
同次線形微分方程式
線形微分方程式で 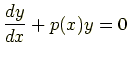 |
(6.11) |
を同次方程式という (斉次方程式ともいう).これは変数分離形であるので,
| (6.12) | ||
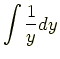 |
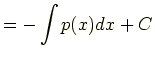 |
(6.13) |
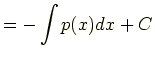 |
(6.14) | |
| (6.15) |
と一般解が求まる. 変数分離形なのにわざわざ同次方程式と別の名前を付けているのは, つぎの非同次方程式を解くときに同次方程式の考えが必要だから.
非同次線形微分方程式
線形微分方程式で
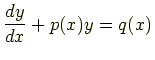 |
(6.16) |
を非同次方程式という (非斉次方程式ともいう).非同次方程式は
| (6.17) |
という形になる. あとは
例
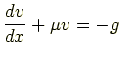 |
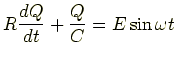 |
物理のかぎプロジェクト / 平成19年1月14日