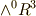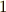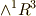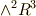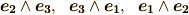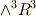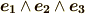軸性ベクトルと擬スカラーの秘密

三次元ユークリッド空間上の外積代数は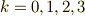， k=0,1,2,3 の４つのベクトル空間 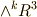$\land ^{k}R^{3}$ の直和になっているということでした．

$R^{3}$ 上の外積代数
外積空間	基底	次元
$\land^{0} R^{3}$
$\land^{1} R^{3}$	$\bm{e_{1}},\bm{e_{2}},\bm{e_{3}}$
$\land^{2} R^{3}$	$\bm{e_{2}}\land \bm{e_{3}}, \ \ \bm{e_{3}}\land \bm{e_{1}}, \ \ \bm{e_{1}}\land \bm{e_{2}}$
$\land^{3} R^{3}$	$\bm{e_{1}}\land \bm{e_{2}}\land \bm{e_{3}}$

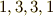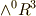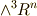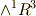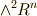そして，各空間の次元は二項係数で表わされるため， 1,3,3,1 と，対称な並びになっています．このため，次元の等しい $\land^{0}R^{3}$ と $\land^{3}R^{n}$ ，そして $\land^{1}R^{3}$ と $\land^{2}R^{n}$ をそれぞれ関係付ける同型写像が存在し，それをホッジ作用素と呼びました．同型写像が存在するということは，数学的に非常に乱暴な言い方をすれば，『同じ次元の外積空間を同じだと見なせる』ということです．（でも，本当は同じではないのです．）この辺りの事情を，この記事では少し考えてみます．

ベクトルの外積と軸性ベクトル

本当のベクトルとは，ベクトルの座標成分は座標系の取り方によるものの，そのベクトルの存在そのものとでも言う実在は座標系にはよらない，実体のある存在なのでした．（このことはベクトル解析分野で何度も強調してきました．例えばベクトルことはじめ（数学）や基底の座標変換を参照下さい．）

ところが，ベクトルにはもう一種類，座標系の取り方に応じて向きを変える変な奴がいました．このため，前者を 極性ベクトル ，後者を 軸性ベクトル と呼んで区別しました．軸性ベクトルには 擬ベクトル という別名もあって，名前からして，なんだかアヤシイ奴だと思った人が多いと思います．擬は難しい漢字ですが，例えば，虫が木の葉そっくりの姿をして敵に見つかりにくくするような工夫を擬態と言うように，字面からは，なんだか『ニセモノが上手に化けている』という意味が嗅ぎ取れます．

バイオリン虫はバイオリンに化けているんじゃない．葉っぱに化けている．でも，上手な擬態だ．（本文の内容とは全く関係ありません．）

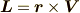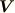軸性ベクトル（擬ベクトル）とは外積の形で与えられるベクトルで，例えば角運動量 $\bm{L}=\bm{r} \times \bm{V}$ は軸性ベクトルでした． $\bm{r}$ や $\bm{V}$ が定義されている空間を 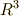$R^{3}$ とし，その基底を 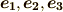$\bm{e_{1}},\bm{e_{2}},\bm{e_{3}}$ とします．そして，ボリューム・フォームを 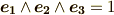$\bm{e_{1}} \land \bm{e_{2}} \land \bm{e_{3}}=1$ と決めます．これで空間の向きを決めましたので，ホッジ作用素が使えます．では，ホッジ作用素の最後の『具体例』で見たことの繰り返しになりますが，もう一度外積代数の視点から角運動量を考えてみましょう．ホッジ作用素をきちんと理解できているかの確認にもなると思います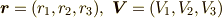． $\bm{r}=(r_{1},r_{2},r_{3}), \ \bm{V}=(V_{1},V_{2},V_{3})$ として，ベクトルの外積 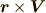$\bm{r} \times \bm{V}$ を求めてみます．

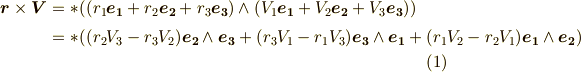
$\bm{r} \times \bm{V} & = *((r_{1}\bm{e_{1}}+r_{2}\bm{e_{2}}+r_{3} \bm{e_{3}})\land (V_{1}\bm{e_{1}}+V_{2}\bm{e_{2}}+V_{3}\bm{e_{3}}) ) \\ &= *((r_{2}V_{3}-r_{3}V_{2})\bm{e_{2}}\land \bm{e_{3}} + (r_{3}V_{1}-r_{1}V_{3})\bm{e_{3}} \land \bm{e_{1}} + (r_{1}V_{2}-r_{2}V_{1}) \bm{e_{1}} \land \bm{e_{2}}) \tag{1}$

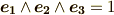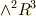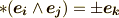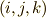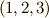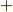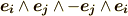最初の行は，ベクトルの外積の定義になっています．そして，二行目への変形は，ウェッジ積の演算なので，大丈夫だと思います．さて，ホッジ作用素の作用ですが，いま空間の向きを $\bm{e_{1}} \land \bm{e_{2}} \land \bm{e_{3}}=1$ と取っているので，例えば $\land^{2}R^{3}$ の基底への作用 $*(\bm{e_{i}} \land \bm{e_{j}}) = \pm \bm{e_{k}}$ を考えるとき， (i,j,k) の並びが (1,2,3) の偶置換なら，奇置換ならを取るのでした．（もっとも $\bm{e_{i}} \land \bm{e_{j}} \land - \bm{e_{j}} \land \bm{e_{i}}$ が成り立つので，奇置換のものは考えなくて済みます．とにかく，添字の順列に注意して下さい．）基底へのホッジ作用素の作用は，次のようになります．

$*(\bm{e_{1}} \land \bm{e_{2}} ) = \bm{e_{3}} \tag{2-1}$

$*(\bm{e_{2}} \land \bm{e_{3}} ) = \bm{e_{1}} \tag{2-2}$

$*(\bm{e_{3}} \land \bm{e_{1}} ) = \bm{e_{2}} \tag{2-3}$

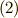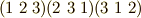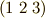式 (2) に現われている添字の順列 $(1 \ 2 \ 3)(2 \ 3 \ 1)(3 \ 1 \ 2)$ が，どれも $(1 \ 2 \ 3)$ の偶置換であることを確認して下さい．これらを式 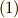(1) に代入することで，次式を得ます．

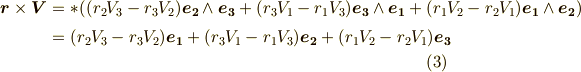
$\bm{r} \times \bm{V}&= *((r_{2}V_{3}-r_{3}V_{2})\bm{e_{2}}\land \bm{e_{3}} + (r_{3}V_{1}-r_{1}V_{3})\bm{e_{3}} \land \bm{e_{1}} + (r_{1}V_{2}-r_{2}V_{1}) \bm{e_{1}} \land \bm{e_{2}}) \\&= (r_{2}V_{3}-r_{3}V_{2})\bm{e_{1}}+ (r_{3}V_{1}-r_{1}V_{3})\bm{e_{2}} + (r_{1}V_{2}-r_{2}V_{1}) \bm{e_{3}} \tag{3}$

私達のよく知っている角運動量の形になりました．ここまでの議論で，最初に決めたボリューム・フォームの向き 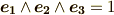$\bm{e_{1}} \land \bm{e_{2}} \land \bm{e_{3}}=1$ は，実は私達が勝手に決めたものでした．（しかし，何の話をするにせよ，一番最初の基準になる部分は，勝手に決めないと始まらないですよね．）これを，例えば 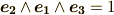$\bm{e_{2}} \land \bm{e_{1}} \land \bm{e_{3}}=1$ と決めたって良いのです．すると，式 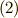(2) は次のようになります．

$*(\bm{e_{1}} \land \bm{e_{2}} ) = - \bm{e_{3}} \tag{2-1}$

$*(\bm{e_{2}} \land \bm{e_{3}} ) = - \bm{e_{1}} \tag{2-2}$

$*(\bm{e_{3}} \land \bm{e_{1}} ) = - \bm{e_{2}} \tag{2-3}$

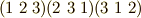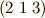添字の順列 $(1 \ 2 \ 3)(2 \ 3 \ 1)(3 \ 1 \ 2)$ が，どれも $(2 \ 1 \ 3)$ の奇置換なので，右辺にはマイナスがつく訳です．このとき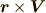， $\bm{r} \times \bm{V}$ は次式のようになりますね．

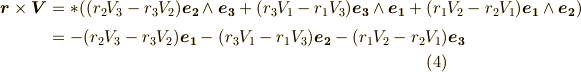
$\bm{r} \times \bm{V}&= *((r_{2}V_{3}-r_{3}V_{2})\bm{e_{2}}\land \bm{e_{3}} + (r_{3}V_{1}-r_{1}V_{3})\bm{e_{3}} \land \bm{e_{1}} + (r_{1}V_{2}-r_{2}V_{1}) \bm{e_{1}} \land \bm{e_{2}}) \\&= -(r_{2}V_{3}-r_{3}V_{2})\bm{e_{1}}- (r_{3}V_{1}-r_{1}V_{3})\bm{e_{2}} - (r_{1}V_{2}-r_{2}V_{1}) \bm{e_{3}} \tag{4}$

式 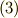(3) で得た結果と符合が逆になってしまいました．もう，カラクリが分かってきたと思いますが，頭を整理するために，内容を整理しておきます．

最初の空間の向き（基底の並べ方）の決め方には任意性がある．
ホッジ作用素が基底に作用するとき，基底の並びが空間の向きに対して偶順列か奇順列かによって，符号が変わる．
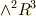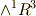ベクトルの外積 $\times$ とは， $\land^{2}R^{3}$ から $\land^{1}R^{3}$ へのホッジ作用素による写像であった．
だから，ボリュームフォームの符号を変えるような座標変換を行うと，ベクトルの外積（軸性ベクトル）も，それに応じて符号を変えてしまう．

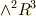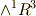軸性ベクトルの符号の問題は， $\land^{2}R^{3}$ の元を $\land^{1}R^{3}$ へ写像する際のホッジ作用素の符号が原因だったのです．

Important

軸性ベクトルとは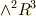， $\land^{2}R^{3}$ の元をホッジ作用素によって 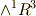$\land^{1}R^{3}$ へ写像したものです．（基底の取り方を変えると，この写像の際に符号が逆になってしまいます．）極性ベクトルとは，もとから 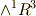$\land^{1}R^{3}$ の元であるベクトルのことです．

高校数学の段階では，外積代数の話は難しすぎますから，極性ベクトルも軸性ベクトルもおなじ 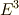$E^{3}$ の元で，なんだか性質が違うんだ，というようにお茶を濁して置くしかなかったわけですが，ここまで読んだ読者のみなさんは，もう秘密が分かったと思います．極性ベクトルとは，最初からら 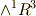$\land^{1}R^{3}$ の元であるベクトル，軸性ベクトルとは本来は 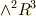$\land^{2}R^{3}$ の元であると見る方が自然なベクトルのことだったのです．

[*]	『写像して二つの空間を同じだと見る』という操作は，『二つの空間を重ね合わせて見てしまう』と表現しても良いでしょう．例えばセル画や写真のネガ（←最近ではあまり見なくなりましたね）を二枚重ねて見てみる場合，まっすぐ重ねる重ね方と，表裏を逆にして，全てアベコベにするような重ね方とがあることが想像つくと思います．この比喩は，あまり正確なものではないかも知れませんが，イメージとしてはこんな感じです．元々違うものを，重ねて一つに見ているんだ，という構造を理解して下さい．

擬スカラー

擬スカラーも同じように考えることが出来ます．擬スカラーとは座標系の取り方を右手系⇔左手系と変えると，その符号を変えるスカラーのことでした．ベクトルの三重積によって定義される体積がその例です．擬スカラーの正体は，本来は 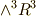$\land ^{3}R^{3}$ の元だと考えるのが自然な元を，ホッジ作用素によって 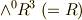$\land^{0}R^{3} \ (=R)$ へ写像したものです．

Important

擬スカラーとは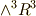， $\land^{3}R^{3}$ の元をホッジ作用素によって 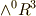$\land^{0}R^{3}$ へ写像したものです．（基底の取り方を変えると，この写像の際に符号が逆になってしまいます．）本当のスカラーとは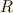，の本当の元のことです．

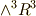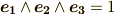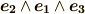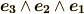スカラーが座標の取り方に応じて符号を変えると言われれば奇妙ですが（だって，スカラーは座標変換によらない量という定義でした），これが $\land^{3}R^{3}$ の元ならば，最初に決めたボリュームフォームに応じて， $\bm{e_{1}} \land \bm{e_{2}} \land \bm{e_{3}} =1$ が右手系ならば， $\bm{e_{2}} \land \bm{e_{1}} \land \bm{e_{3}}$ や $\bm{e_{3}} \land \bm{e_{2}} \land \bm{e_{1}}$ 等は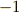となりますから，納得のいく話です．

[†]

軸性ベクトルや擬スカラーの怪しい挙動は，本当は違うベクトル空間の元を，次元が同じなのをいいことに，無理やり同じベクトル空間上の元だと見ようとしたことに原因があります．ホッジ作用素そのものは，別に怪しいものでも何でもありませんから，きちんと使えば良いのです．悪いのは，きちんとこの辺りの事情を説明しなかった学校の先生です．といっても，大抵の人はベクトルの外積は高校で習いますが，いきなり高校生に『本当は違うベクトル空間が云々・・・』と講釈しても混乱を拡大するだけでしょうから，『ベクトルには二種類ある云々』と教えるのもしょうがないことです．それでも，やはり理系の大学では大学一・二年生くらいできちんと外積代数を勉強して，この辺りの事情を明快にしておくべくだと思います．

[home] [微分形式] [ページの先頭]