基底の座標変換
ベクトルの成分は座標系の取り方によって変わります.

図はそれほど正確ではありませんが,青いベクトルは全く動いていないのに,点線(座標軸)に射影した長さは,座標系の取り方によって全く異なることが理解できると思います.
| [*] | ベクトルの座標変換と聞いたときに,『ベクトルを動かす』というイメージを持っている人がいるかも知れません.考え方として,これは逆なのですが,実際,観測者の気持ちになってみれば,ベクトルの見え方が変わったのですから,『ベクトルの方が動いた』と感じるのは当然です.しかし,ベクトルが数学的な対象物として,人間の意志とは別に厳然とそこに存在する物なのに対し,座標系は見る人が便利なようにどこに取っても良いものなのですから,ベクトルは動かず,見る人が視点を変えたと考えるのが正確です.この区別は観測者からだけでは分かりませんので,『本当にベクトルが動いた』場合と『座標の取り方が変わった』場合の計算結果は,観測者からだけでは区別できないと言わざるをえません.ちょうど天動説と地動説のようなものです.回転している人が遠心力を『本当の力』のように感じてしまうのも同じ事情によるものです.座標系にとらわれて視野がゆがむというのは恐ろしいことです. |
さて,ある座標系の基底ベクトル  を,
を, 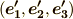 に変換することを考えます.一般に
に変換することを考えます.一般に 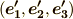 の各ベクトルは
の各ベクトルは  の関数となり,
の関数となり, 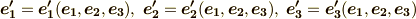 のように書けるはずですが,ここでは次式のように,それぞれ適当な係数を使って
のように書けるはずですが,ここでは次式のように,それぞれ適当な係数を使って 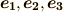 の線形結合で表現できるとします.ここで考えている座標変換とは暗に基底の向きを変えるだけの変換ですので,このように表現できると考えて問題はないでしょう.
の線形結合で表現できるとします.ここで考えている座標変換とは暗に基底の向きを変えるだけの変換ですので,このように表現できると考えて問題はないでしょう.
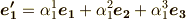
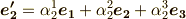
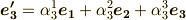
私達はこの係数 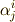 を具体的にはまだ知りませんが,何らかの
を具体的にはまだ知りませんが,何らかの 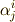 を用いれば,このような式形で座標変換を表現できることまでは諒解して頂きたいと思います.上の三式をまとめて行列表示にしても良いでしょう.
を用いれば,このような式形で座標変換を表現できることまでは諒解して頂きたいと思います.上の三式をまとめて行列表示にしても良いでしょう.
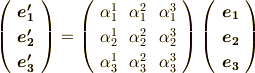
式の中に出てきた係数  を 変換係数 と呼びます.変換係数が,ダッシュの付いていない基底からダッシュの付いた基底への座標変換を決定しています.変換係数につけた添字は,上や下に分けてありますが,この書き方にはちゃんと意味があります.この記事の最後で説明しますので,今はこのように添字を振ることを了承して頂きたいと思います.上の三式をまとめて次のようにも書いても良いでしょう.
を 変換係数 と呼びます.変換係数が,ダッシュの付いていない基底からダッシュの付いた基底への座標変換を決定しています.変換係数につけた添字は,上や下に分けてありますが,この書き方にはちゃんと意味があります.この記事の最後で説明しますので,今はこのように添字を振ることを了承して頂きたいと思います.上の三式をまとめて次のようにも書いても良いでしょう.
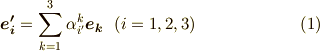
同様にして,ダッシュの付いた基底からダッシュの付いていない基底への変換を表すことも出来ます.
変換係数の性質
式 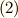 を式
を式  に代入すると次式を得ます.
に代入すると次式を得ます.
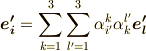
両辺を比べると,『右辺 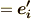 』となるはずですので,係数には次の関係が要請されます.
』となるはずですので,係数には次の関係が要請されます.
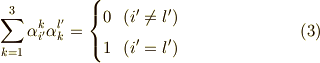
同様に,式  を式
を式 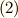 に代入することで,次の関係式を得ます.ダッシュのつく文字が逆になっているだけで,式
に代入することで,次の関係式を得ます.ダッシュのつく文字が逆になっているだけで,式 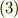 と同じです.
と同じです.
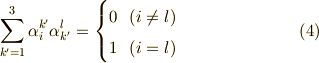
この結果は,何も驚くべきものではありません.変換と逆変換を連続して行えば,もとの座標系に戻るはずで,自分自身への座標変換,つまり全く動かない一次変換を表わす行列は単位行列のはずです.式 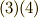 はそのことを表わしているに過ぎません.添字がごちゃごちゃして意味が分かりにくかった人がいるかも知れませんが,要するに次式の行列の成分を,
はそのことを表わしているに過ぎません.添字がごちゃごちゃして意味が分かりにくかった人がいるかも知れませんが,要するに次式の行列の成分を,  の条件式として表わしてみただけなのでした.
の条件式として表わしてみただけなのでした.
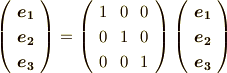
今後,テンソル解析という分野に入ると,もっと面倒な添字の計算がたくさん出てきますから,今のうちに少しずつ慣れていきましょう.
縮約
式 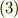 や式
や式 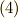 で
で  の記号が出てきましたが,これをいちいち書くのは面倒なので,次のように決めて
の記号が出てきましたが,これをいちいち書くのは面倒なので,次のように決めて  の記号を省略することにします.これを アインシュタインの縮約 と呼びます.
の記号を省略することにします.これを アインシュタインの縮約 と呼びます.
Important
上と下に同じ添字が出てきたら,その添字の総和を取ることとします.
基底  にかかる変換係数で,添字
にかかる変換係数で,添字 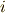 をわざわざ
をわざわざ  のように基底の添字の位置と逆にしたのは,この縮約を使いたかったからなのです.
例えば,式
のように基底の添字の位置と逆にしたのは,この縮約を使いたかったからなのです.
例えば,式 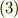 の左辺
の左辺 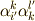 には,上下に分かれて
には,上下に分かれて 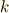 が出てきていますから,縮約に従って自動的に
が出てきていますから,縮約に従って自動的に 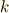 の和を取り,
の和を取り,  を書かなくても
を書かなくても 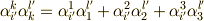 の意味だとします.慣れてくるととても便利です.
の意味だとします.慣れてくるととても便利です.
アインシュタインの縮約を使った例を二つ挙げておきます.添字の上下に気をつけてください.  とします.
とします.
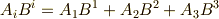
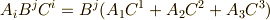
一番目の式はベクトル 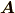 とベクトル
とベクトル 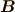 の内積
の内積  を,二番目の式は
を,二番目の式は 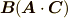 を表わしています.アインシュタインの縮約の規則自体は難しくないと思いますが,多くの人がきっと『添字を上につけたり下につけたりする意味は一体何なの!!?』という,憤懣やる方ない気持ちを抱いていると思います.
を表わしています.アインシュタインの縮約の規則自体は難しくないと思いますが,多くの人がきっと『添字を上につけたり下につけたりする意味は一体何なの!!?』という,憤懣やる方ない気持ちを抱いていると思います.
確かに,高校の数学にも添字は出てきましたが,上につけるか下につけるかには,あまりこだわりませんでした.特に, 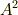 と書いたら『
と書いたら『 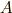 の二乗』と紛らわしいですから,添字は常に右下に書くことにしていた人が多いかも知れません.残念ながら,この記事で添字の上下に関する秘密を全て解説することは出来ません.この添字の仕組みに隠されたベクトルやテンソル(ベクトルの概念を拡張したようなものです)の構造を理解していくのがベクトル代数部門の目標の一つでもあり,時間をかけて解明していく予定だからです.勉強が進むにつれて,だんだんと霧が晴れていくと思いますので,まず今は,縮約の規則だけ覚えればよしとしましょう.
の二乗』と紛らわしいですから,添字は常に右下に書くことにしていた人が多いかも知れません.残念ながら,この記事で添字の上下に関する秘密を全て解説することは出来ません.この添字の仕組みに隠されたベクトルやテンソル(ベクトルの概念を拡張したようなものです)の構造を理解していくのがベクトル代数部門の目標の一つでもあり,時間をかけて解明していく予定だからです.勉強が進むにつれて,だんだんと霧が晴れていくと思いますので,まず今は,縮約の規則だけ覚えればよしとしましょう.
縮約について,もう一点だけ付け加えておくべきことがあります.さきほどの縮約の特別な場合です.
Important
各基底ベクトルが直交するように座標系を取っている場合(直交基底)に限って,上下に分かれてなくても,同じ添字が連続して出てきたら総和を取ることとします.
やはり,理由を全て説明するわけには行きませんが,なぜ直交基底の場合に,こんなことが許されるのかをという事情に簡単に触れておきましょう.これから勉強する内容をある程度俯瞰することにもなると思います.ベクトルにはズバリ,添字が上につく仲間と下につく仲間とがあり,それぞれは一卵性双生児のように対称な世界を形作っています.そして,『添字が上下に分かれた二つのベクトルの内積を取ると,座標変換に対して不変な量になってしまう』という性質があるのです.こんな話を初めて聞いた人はビックリしたかも知れませんが,この世界は実はそんな構造になっていたのです.この理論は,これからゆっくり勉強していきますから,今は何も焦らなくて大丈夫です.さて,直交座標系(基底ベクトルがそれぞれ直交する座標系)の場合に限って,添字が上のベクトルと添字が下のベクトルを区別しなくても良いという事情があり(両者が等しくなってしまうのです),上の規則はこの事情に基づいています.
理論を勉強する前に結果だけ先取りするのは気持ち悪いですが,和を取るたびに  を書くのは面倒ですから,縮約だけは最初に導入しておきたかったのです.
を書くのは面倒ですから,縮約だけは最初に導入しておきたかったのです.
アインシュタインの縮約によって,  を使わずに次式の左辺を右辺のように書いてしまえるのは,座標系を 直交座標系に取った場合だけ です.
を使わずに次式の左辺を右辺のように書いてしまえるのは,座標系を 直交座標系に取った場合だけ です.
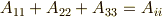
| [†] | 薄ぺったい教科書の中には,添字の上下には触れずに『同じ添字が二回出てきたら和を取る』とだけ書いている悪質なものがあります.確かに,私達が使う座標系のほとんどは直交座標系ですから,そのように覚えておいても実際の計算で困ることはあまり無いでしょう.かえって,急に添字の上下を言い始めると『添字ってそもそも何なの?』『上につく添字と,下につく添字はどう違うの?』『どうして座標変換に対して不変なの?』というような疑問が一挙に噴出して,収拾のつかないことになる可能性もあります.しかし,物理のかぎしっぽの読者諸兄姉は本格派ですから,そのようないい加減な定義には却って納得しないと思い,背後の事情もいきなり説明してみました.この添字の仕組みは非常によく出来ていて,添字の上下の違いにも,数学的・物理的な意味の違いがあることが徐々に分かってきます.テンソルという概念を勉強すると,添字の上と下の意味の違いが更にはっきり分かるでしょう.長い道のりです.次の 共変ベクトルと反変ベクトル で,添字の上下による違いがさっそく出てきます. |
クロネッカーのデルタ
式 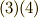 の右辺に『
の右辺に『 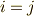 なら
なら 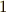 ,
,  なら
なら  』という場合分けが出てきましたが,これを次のような関数で書くと便利です.
』という場合分けが出てきましたが,これを次のような関数で書くと便利です.

これを クロネッカーのデルタ と呼びます.ベクトルやテンソルの計算でとても重宝するものです.添字の上下による区別は,今はあまり気にしないでください.
クロネッカーのデルタとアインシュタインの縮約を用いると,式 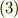 は次のように書けます.随分シンプルになりました!!
は次のように書けます.随分シンプルになりました!!

| [‡] | 急にアインシュタインの名前が出てきましたが,相対性理論で有名なあのアインシュタイン(  )です.相対性理論では座標変換の計算をたくさん行いますが,そこではベクトルを少し拡張したテンソルという概念を多用します.テンソルの計算は添字計算の嵐のようなものです.アインシュタインはテンソル解析の達人だったということですが,彼が )です.相対性理論では座標変換の計算をたくさん行いますが,そこではベクトルを少し拡張したテンソルという概念を多用します.テンソルの計算は添字計算の嵐のようなものです.アインシュタインはテンソル解析の達人だったということですが,彼が  の記号を省略する書き方を最初に始めたそうです.相対性理論は,平たく言えば,座標変換をすると物理量の見え方や物理法則がどう変わるかに関する理論です.時間や空間に関する相対性理論の結果が日常生活の常識からあまりに懸け離れているためか,相対性理論を非常に難解な不可思議な理論だと思っている人が多いようですが,空間と時間を併せた座標系において『座標変換とともに変わるものは何か,座標系によらずに一定なものは何か』を考える理論だと言えば,意外と単純な理論なのではないかとも思えてきます. の記号を省略する書き方を最初に始めたそうです.相対性理論は,平たく言えば,座標変換をすると物理量の見え方や物理法則がどう変わるかに関する理論です.時間や空間に関する相対性理論の結果が日常生活の常識からあまりに懸け離れているためか,相対性理論を非常に難解な不可思議な理論だと思っている人が多いようですが,空間と時間を併せた座標系において『座標変換とともに変わるものは何か,座標系によらずに一定なものは何か』を考える理論だと言えば,意外と単純な理論なのではないかとも思えてきます. |