ベクトルことはじめ（数学）

これからベクトルやテンソル（ベクトルの概念を拡張したようなものです）について勉強していきます．この記事は，この後どのような話題を勉強するのか，どのような点が大事になるのかといったことに関するガイダンスです．

[*]	記事の拡充もしくは執筆計画の変更に伴い，かならずしも，この記事の内容通りには行かないかも知れません．

ほとんどの人が既に高校でベクトルを習ったと思いますが，高校数学で習うベクトルのイメージといえば矢印でしょうか．

ベクトルが矢印かどうかは今は措いておくとして，ベクトルの後ろ，つまり図の真っ白な部分はどうなってるんでしょうか？『どうなってるもなにも，何にも無い！』というのは正しい答ですが，気になるのは，その『空間の構造そのもの』とでも言うものです．

こんな思考実験をしてみましょう．この世から，どんどん物を消していきます．人も消します．はい，地球も無くなりました．星も全部なくします．原子も素粒子も光も，全部取り去ってしまいます．何が残るでしょうか？完全な真空でしょうか？では『真空という概念』さえ取り去ってしまったら，どうなるでしょうか？単なる空っぽ？では，空っぽという概念も取り去ってしまいましょう．・・・・・難しいですね．これは数学というよりは哲学的な問題です．

完全に物理的対象を除いてしまったら，空っぽの空間だけが残ると考える人がいるかも知れません．しかし，その空間に「広がり」はあるのでしょうか？というのは，最低限二つの点がこの世に存在しなければ，距離という物を定義しようがないし，定義できなければ概念さえ存在しえないと考える立場もあるからです．

どうなんでしょうかね．「広がりという概念は，最低二つの物があって後に生まれる」と考えたのはドイツの哲学者・数学者ライプニッツ( $\text{Gottfried Wilhelm Leibniz (1646-1716)}$ )です．興味のある人は，例えば世界の名著を読んでみて下さい．

微積分学の創始者ライプニッツ．哲学者でもあった．ライプニッツのモナド論には，意外と現代物理学に通じるところがありそうだ．

ここでは，あまりこの話題に深入りはしません．どうやら「空間に広がりがある」ということも，それほど自明じゃないぞ！？ということに気がついていただければ十分です．

ユークリッド空間

数学では，よく分からないことは事前にきちんと約束をしておかなければなりません．そこで これから考える空間には『距離という概念』がある と決めておきます．

一個のベクトルさえ存在しないこの真っ白（空間に色はあるのか？？）な空間には，きちんと距離があります．距離があるということは 角度も測れます ．

[†]	しかし『距離をどのように定義するか』というのは，また別の難しい問題です．数学的に正確には，空間に計量が定義されていると言います．内積空間で少しこの話題に触れます．

かなり幾何学ができそうな雰囲気になってきました．もう一つ決めておくのは，この空間そのものは 一様で等方的 だということです．つまり，空間そのものに前後左右上下の区別はなく，どっちを向いても，どこに行っても，空間そのものは同じだということです．そうしておかないと，場所や向きによって図形の性質が変わって来てしまうからです．

それから，先ほど，距離の概念を入れましたから，空間には広がりがありますが，ではどのような広がり方をしているのでしょうか？ここには色々な議論がありそうですが，しばらくは空間を三次元だと考えることにします．つまり 空間内のどの点も，三つの数の組を選ぶことで一意的に示せる と約束するわけです．ここで使う数は実数とします．

ベクトルが一個もない「空っぽな」空間でも，既にこれぐらいのことを約束して決めておくわけです．

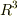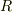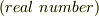『３つの実数でどの点も示せるよ』という意味で，この空間を $R^{3}$ と書くこともあります．は実数 $(real \ number)$ の意味です．空間の話が少し長くなりましたが，いよいよこの空間にベクトルを置いてみましょう．

うーん，やはり何か物があると良いですね．

[‡]	数学を専門にしている人は，もう少し厳密に空間について決め事をしておかなければならないようです．今は，あまり難しいことにこだわらずに先に進みましょう．

座標系

さて､空間にいよいよベクトルが登場してきました．『そもそも，なぜ，ベクトルはあるんだ？』『本当にそこにベクトルはあるのか？』という問いに対しては，『ベクトルはそこにあるのです』と答えることにしましょう．（ちょっと不本意ですが）神様がそこに置いた，とでも言うしかありません．とりあえず，私達の都合とは関係なく，"そこにベクトルは存在する"と考えます．

ここからは，私達サイドの問題です．ベクトルの長さを測ったり，位置を決めたりするのに，空間をどのように測ったら良いのでしょうか？とりあえず，３つの実数の組を，空間の任意の一点に割り当てるためのシステムが必要です．このシステムのことを 座標系 と呼びます．要点は，『うまく空間の一点に３つの実数の組を対応させられれば，座標系の取り方は自由だ』ということです．座標系の取り方は私達「観測者側の都合」ですから，ベクトルには何の関係も責任もない話なのです．

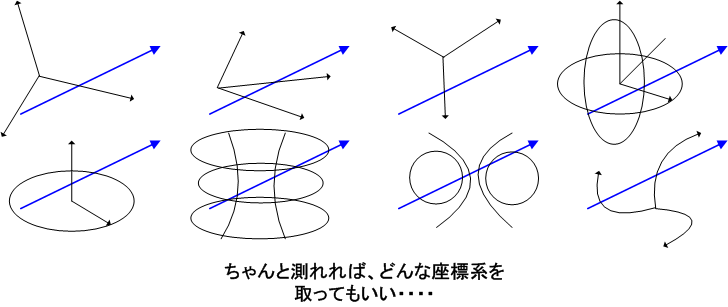
座標系とは，私たちが図形の上に勝手に押し付けた定規のようなものです．どこから見るか，どうやって見るか，どのように測るか，によってベクトルの「見え方」は変わってきます．特に，途中で座標系を変えた場合（座標変換と言います），いきなり見え方が変わります．しかし，『ベクトルそのもの』という数学的実体は，そのような観測者の都合とは無関係で，不変のはずです．もう少し突っ込んで言うと，ベクトルそのものは座標変換には無関係ですが，ベクトルの成分（見え方）は座標系によって変わります．

これは，今後のベクトルの勉強で，とても大事な問題です．

Important

座標変換したとき，何が変わるか，何が変わらないか．

基底を意識しよう

高校までは，座標系と言ったらほとんどの場合，次図のようなデカルト座標系のことでした．つまり，まっすぐな 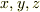x,y,z 軸が互いに直交するように交わっているものです．

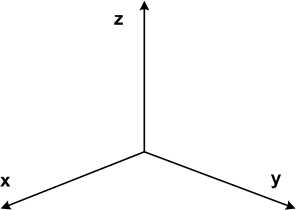
確かにデカルト座標系は便利ですが，『座標系は私達が勝手に選ぶもの』という視点から言えば，いつもいつもデカルト座標系に決まっていると考えるのは本末転倒です．私たちは，いつでも 一番便利な座標系を選んで良い のです．

ベクトルを 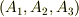$(A_{1},A_{2},A_{3})$ のように成分の組として計算することがありますが，一体どの座標系で測った場合の成分なのかを考えずに計算していたのでは，単に３つの数字の組を計算しているだけに過ぎません．一番大事なことは成分ではありません．座標系の選び方です．そこで高校数学のように 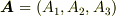$\bm{A}=(A_{1},A_{2},A_{3})$ とは書かず，座標の基底ベクトルが明示的に分かる，次のような書き方の方が便利な場合が多々あります．

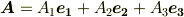
$\bm{A} = A_{1}\bm{e_{1}}+ A_{2}\bm{e_{2}}+ A_{3}\bm{e_{3}}$

使っている座標系がよほど明らかな場合には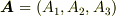， $\bm{A}=(A_{1},A_{2},A_{3})$ のように書いても構いませんが，それでは単に三つの数の組を計算しているのとあまり変わりませんし，エキサイティングじゃありません．

Important

いま，どんな座標系で考えているのかが大事．

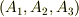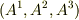[§]	もう一つ付け加えると，いまベクトル成分の添字を $(A_{1},A_{2},A_{3})$ のように下につけましたが，今後 $(A^{1},A^{2},A^{3})$ のように上につけることが多くなります．共変ベクトルと反変ベクトルでこのことの説明をします．

微分

ベクトルを微分したり積分したりすることがあります．いま，関数をある方向に空間微分することを考えてみましょう．微分の意味は『その方向に沿って関数がどう変化するか？』を調べることですから，言うまでも無く，微分する方向と導関数とは切っても切れない関係にあります．ベクトルの微積分をするときに，微分する向き，つまりどの方向の変化を調べるかを忘れてはいけません．

ベクトルの微積分にも色々な場合がありますが，例えば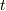の関数であるベクトル 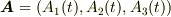$\bm{A}=(A_{1}(t),A_{2}(t),A_{3}(t))$ を微分する場合，計算自体は，成分毎に微分をすればいいので，関数を三つ微分するのと同じで特に難しいことはありません．しかし，ベクトルの微分を，単に「手間が三倍の微分計算」だと思ってしまっては，全く木を見て森を見ずです．

Important

微分は向きが命です．ここでも座標系（変数）をどう取るかが，とてもとても重要です．

このように，導関数の値は一般には座標系の取り方によりますが，中には座標系の取り方によらない導関数もあります．そんなものを考えるのも，ベクトル解析の醍醐味です．

Important

ベクトルを微積分するとき，座標系によるものは何か，座標系によらないものは何か．

代数構造

ベクトルには『足し算』『引き算』が定義できます．それから『内積』『外積』といった計算がありました．そのうちテンソル積という名前の掛け算も出てきます．

つまり，ベクトルを全部を集めて集合を作ると，この集合は単にそこら辺の物を寄せ集めてきて作った集合とは異なります．ちゃんと『集合の中で計算ができる』のです．少し違う言い方をすれば，ベクトル全体の集合とは『演算規則という構造を備えた集合』であると言えます．このような，集合に備わった計算規則の構造を 代数構造 と呼びます．

さらに，もしベクトルの集合と全く同じ計算構造を備えた集合があれば，集合の元が何であるかには関わらず，計算の仕方に関して全く同じ議論ができるはずですから，『演算規則という構造だけ』を抜き出して抽象的な議論をすることにも意味がありそうです．

こうなると，もう矢印でイメージしていたベクトルの話ではなく，完全に抽象的な集合の話になってしまいます．抽象的な数学が苦手な人も多いと思いますが，このような抽象的な議論の目的は，単にベクトルの計算結果を他の集合へ適用することだけではありません．

むしろ『集合そのもの』の性質を考えることで，より深遠な，世界のカラクリとも言うべき美しい構造が背後に見えて来たりします．また，『まるで関係ないと思われていた物の間に，実は数学的に密接な関係がある！』といった不思議なつながりが，抽象的な議論を通じて美しく炙り出されて来ることもあるのです．

いつまでも，ベクトルを矢印のイメージで捉えていると，そのうち想像力に限界が来て，抽象的な議論についていかれなくなります．ときには，分かりやすい矢印のイメージを潔く捨てることも大事です．

Important

ベクトルが，いつも矢印だとは限らない．

例えば，ベクトルの加法やスカラー積の概念を抽象化したベクトル空間という集合では，関数，多項式，演算子，行列など，色々なものが元になる可能性があります．とても，矢印のイメージで対応しきれるものではありません．

[¶]	ベクトル同士を足したり，ベクトルを定数倍してもベクトルですが，この性質を抽象化した集合をベクトル空間と呼びます．ベクトル空間とは，ベクトルの持つ演算の規則だけを抽象化した概念ですから，同じような演算を満たす物があれば，何だってベクトル空間を作ることが出来ます．上で述べたことは，一般のベクトル空間の元は矢印に似ているとは限らない，ということです．抽象数学は簡単ではありませんが，少しずつ慣れていきましょう．

その先の展望

ベクトルの分野で，ベクトルの計算そのものも非常に重要ですが，ここまで強調してきたように，ベクトルの計算を通じて，座標系，座標変換，座標変換で変わるもの，座標変換で変わらないもの，といった内容について理解を深められればさらに意義深いと思います．また，ベクトルの概念を拡張した，テンソルというものも勉強します．

座標変換で変わらないものを突き詰めて行くと，微分形式という理論に至ります．物理の法則では，保存量という考え方が非常に大事です．また，例えば相対性理論の枠組みでは，質量や時間は座標変換に応じて変化するのに対し，光速は座標変換によらないと主張されています．あらかじめ座標変換の達人になっておくと，そんなことがとても見通しよく理解できるようになります．

一方，そもそも座標変換って何なんだ？座標系って何なんだ？という疑問を突き詰めて行くと，多様体という概念に行き着きます．多様体とは，その上の一点で座標系を取れる（とても大きな）図形で，座標変換することは，多様体の上をちょこっと移動するのと同じことになります．これ以上，ここで乱暴な説明をするのは止しておきます．多様体はなかなか奥が深く，難しい概念ですが，現代の数学では，幾何学をするために無くてはならない重要な概念となっています．微分形式の理論にも多様体は必須になってきます．ベクトル解析の議論の延長で，なんとかそのあたりまで話が広がれば良いと思っています．

[home] [ベクトル解析] [ページの先頭]