可解群について補足
有限群 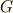 の部分群の組成列を考えるとき,隣り合う群の商群
の部分群の組成列を考えるとき,隣り合う群の商群 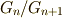 が全て可換群になるとき,
が全て可換群になるとき, 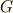 を 可解群 と呼ぶのでした.
を 可解群 と呼ぶのでした.
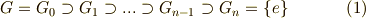
可解群の定義だけは 組成列と単純群 で紹介していますが,その役割については何も触れませんでした.名前から察せられるように,方程式の可解性を考えるときに重要な概念なのです.この記事では,後でガロア理論で使うために必要な,可解群に関する定理を導いておきます.二つ定理を紹介しますが,二番目の方が特に重要です.
theorem
群 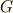 の正規部分群を
の正規部分群を 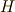 とします.
とします. 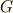 が可解群となるのは,
が可解群となるのは, 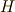 および
および 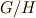 が可解群になる場合に限ります.
が可解群になる場合に限ります.
proof
式 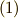 の組成列を考えて,
の組成列を考えて, 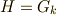 だと仮定します.すると
だと仮定します.すると 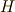 の組成列として
の組成列として 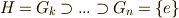 を考えることが出来ます.また,商群
を考えることが出来ます.また,商群 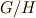 の組成列は
の組成列は 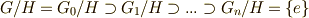 で与えられます.ここで 第三同型定理 を使うと
で与えられます.ここで 第三同型定理 を使うと 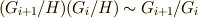 が言えますので,結局
が言えますので,結局 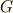 の組成列の要素である各
の組成列の要素である各 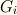 は,
は, 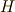 や
や 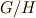 の組成列でも全く共通だということが示されます.これより定理が成り立つの明らかです.■
の組成列でも全く共通だということが示されます.これより定理が成り立つの明らかです.■
次の記事, ガロア群と可解群 の定理の証明では,次の定理を活用します.
theorem
有限巡回群は可解群です.
proof
証明は数学的帰納法によります.巡回群が一般に可換群であることより,位数が 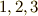 までの有限巡回群は,正規部分群として
までの有限巡回群は,正規部分群として 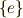 しか含まないので,可解群になることは自明です.一般に,位数が
しか含まないので,可解群になることは自明です.一般に,位数が 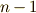 までの巡回群が可解群になると仮定しましょう.このとき,位数
までの巡回群が可解群になると仮定しましょう.このとき,位数 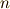 の有限巡回群
の有限巡回群 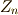 に対し,もし
に対し,もし 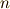 が素数ならば,
が素数ならば, 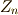 の正規部分群は
の正規部分群は 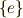 だけとなり,定理は自明です.
だけとなり,定理は自明です. 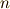 が素数ではないとして,
が素数ではないとして, 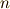 が素数
が素数 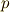 で割り切れるとすると, シローの定理 により,
で割り切れるとすると, シローの定理 により, 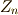 は位数
は位数 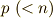 の部分群
の部分群 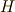 を持ちます.特に
を持ちます.特に 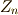 は可換群ですから,
は可換群ですから, 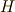 は正規部分群で,このとき仮定より
は正規部分群で,このとき仮定より 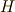 は可解群となり,
は可解群となり, 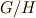 も可換群になります.■
も可換群になります.■
まだ,この段階では定理の使い方がピンと来ないと思いますが,ゆっくりゆっくり進んで行きましょう.