ガロア群と可解群
復習になりますが,体 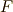 の代数方程式
の代数方程式 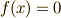 が解の公式を用いて解けるとは,『加・減・乗・除の四つの演算と,開冪(根号を取ること)により,
が解の公式を用いて解けるとは,『加・減・乗・除の四つの演算と,開冪(根号を取ること)により, 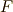 上の数を有限回組み合わせることで解を表現できる』という意味です.
上の数を有限回組み合わせることで解を表現できる』という意味です.
五次方程式に解の公式が存在しないことはアーベルによって証明されましたが,方程式の可解性についてより包括的に一般論を完成させたのはガロア(  )です.ガロアは高校で数学を始め,わずか
)です.ガロアは高校で数学を始め,わずか 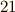 歳にして決闘に斃れますので,実質的に数年間しか数学の勉強をしていないわけですが,ガロアがいなければ数学が
歳にして決闘に斃れますので,実質的に数年間しか数学の勉強をしていないわけですが,ガロアがいなければ数学が 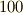 年は遅れていたであろうというほどの貢献をしました.ガロアの人生については,また後に触れます.実は,ガロアが高校生のとき,ノルウェー人のアーベルは一回パリを訪れています.恐らく,直線距離で二人の間は数キロと離れていなかったと想像されますが,もちろん当時はこの二人が方程式の可解性について決定的な仕事をすることをお互いに知りませんでした.
年は遅れていたであろうというほどの貢献をしました.ガロアの人生については,また後に触れます.実は,ガロアが高校生のとき,ノルウェー人のアーベルは一回パリを訪れています.恐らく,直線距離で二人の間は数キロと離れていなかったと想像されますが,もちろん当時はこの二人が方程式の可解性について決定的な仕事をすることをお互いに知りませんでした.

ちょっと変わった顔だ.
円分体で復習
既に 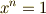 という円周等分方程式の解については, 1のn乗根 , 作図できる正多角形 , 正五角形の作図 , 正十七角形の作図 で議論を重ねてきましたので,一般の方程式に進む前にもう一度円周等分方程式から議論をスタートさせましょう.
という円周等分方程式の解については, 1のn乗根 , 作図できる正多角形 , 正五角形の作図 , 正十七角形の作図 で議論を重ねてきましたので,一般の方程式に進む前にもう一度円周等分方程式から議論をスタートさせましょう.
まず 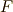 上の円周等分方程式
上の円周等分方程式  を復習します.
を復習します. 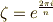 とすると,他の解は
とすると,他の解は 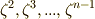 と与えられるところまでは大丈夫でしょう.次に,
と与えられるところまでは大丈夫でしょう.次に, 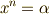 という,右辺が
という,右辺が 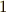 ではない方程式を考えてみます.基本的な解の振る舞いは同じで,一つの解を
ではない方程式を考えてみます.基本的な解の振る舞いは同じで,一つの解を  とすると,他の解は
とすると,他の解は  で与えられることになります.(
で与えられることになります.(  は
は  と
と 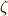 を掛けた形になっている訳です.)
を掛けた形になっている訳です.)
このとき,もし  の最小分解体
の最小分解体 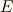 が
が  と
と 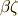 を含めば,
を含めば, 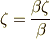 より
より 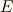 は
は 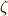 も含むこととなり,このようにして全ての解
も含むこととなり,このようにして全ての解  が表現できます.そこで,
が表現できます.そこで, 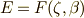 が言えるでしょう.
が言えるでしょう.
| [*] | 直観的イメージとして,半径  の円上に解がグルリと並んでいる様子を想像して下さい.最初の解を の円上に解がグルリと並んでいる様子を想像して下さい.最初の解を  とすると,次の解は とすると,次の解は 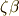 で表わされます. で表わされます. 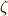 の偏角は の偏角は 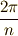 度です. 度です.  から始めて順次 から始めて順次 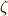 を掛けていくことで,全ての解を表わせるようになっています. を掛けていくことで,全ての解を表わせるようになっています. |

このとき, 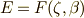 は
は 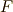 上既約な多項式
上既約な多項式 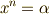 の最小分解体ですので,
の最小分解体ですので, 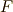 のガロア拡大になっています.( 対称式への応用 参照.)
のガロア拡大になっています.( 対称式への応用 参照.) 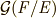 の元は
の元は 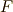 を固定体に保つ同型写像で,
を固定体に保つ同型写像で, 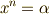 の解
の解 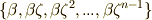 を置換します.これは例えば
を置換します.これは例えば 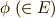 に対して,
に対して, 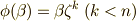 を満たす
を満たす 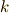 が一つ決まり,かつ
が一つ決まり,かつ 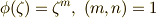 を満たす
を満たす 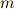 も一つ決まるということです.( 1のn乗根 参照.)
も一つ決まるということです.( 1のn乗根 参照.)
ここで, 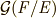 について次の定理がなりたちます.可解群の定義を忘れてしまった人は 組成列と単純群 を参照して下さい.
について次の定理がなりたちます.可解群の定義を忘れてしまった人は 組成列と単純群 を参照して下さい.
theorem
体 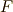 上の多項式
上の多項式 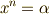 の最小分解体を
の最小分解体を 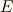 とするとき,ガロア群
とするとき,ガロア群 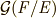 は可解群になります.
は可解群になります.
proof
ここまでの議論と記号を使い, 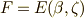 と表わします.
と表わします. 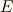 と
と 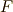 に対して中間体
に対して中間体 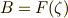 を考えると,
を考えると, 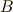 は
は  の最小分解体なので
の最小分解体なので 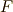 のガロア拡大で, ガロア理論の基本定理 により,
のガロア拡大で, ガロア理論の基本定理 により,  は
は 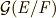 の正規部分群になります.
の正規部分群になります.  の元となるのは,
の元となるのは, 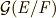 の元である同型写像のうち,
の元である同型写像のうち, 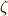 を動かさない写像だけです.つまり,
を動かさない写像だけです.つまり, 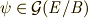 に対し,
に対し,  が言えます.(一般に
が言えます.(一般に 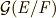 の元は
の元は 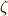 を
を 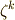 (ただし,
(ただし, 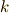 と
と 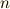 は互いに素)に移すわけですが,特に
は互いに素)に移すわけですが,特に  の場合が
の場合が  の元だと考えられます.)引き続き,
の元だと考えられます.)引き続き,  の元
の元 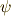 を考えます.
を考えます. 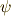 は
は  に対しては
に対しては  のような写像として働きますが(∵
のような写像として働きますが(∵ 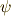 は
は 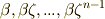 を互いに置換するからです),写像の一意性により,逆にこの指数
を互いに置換するからです),写像の一意性により,逆にこの指数 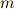 によって
によって 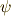 を特定することが可能です.よって,
を特定することが可能です.よって,  の元を
の元を 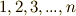 に一対一対応させることができ,実際,
に一対一対応させることができ,実際, 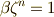 より, 有限巡回群
より, 有限巡回群  は
は 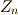 と同型だと言えます.ここで 可解群について補足 で証明した定理を用いると,
と同型だと言えます.ここで 可解群について補足 で証明した定理を用いると,  は可解群だということが分かります.さて,
は可解群だということが分かります.さて, 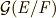 の元(
の元( 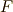 を不動に保つ
を不動に保つ 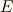 の同型写像)のうち,
の同型写像)のうち, 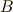 を
を 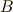 自身に写す部分群を考えれば,それが
自身に写す部分群を考えれば,それが 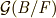 だと言えます.
だと言えます. 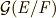 の元
の元  のうち,特に
のうち,特に 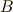 を
を 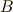 自身に写すものを
自身に写すものを 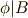 と書くことにすると,
と書くことにすると,  という写像は,元について
という写像は,元について  と表わせることが分かります.さて,
と表わせることが分かります.さて, 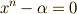 の解を
の解を 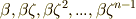 とすると,一般に
とすると,一般に  はこの解を置換し,適当な整数
はこの解を置換し,適当な整数 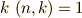 を使って,その作用を
を使って,その作用を 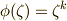 と書けたわけですが,この
と書けたわけですが,この 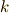 を決めることで,
を決めることで,  という写像を決定することが可能なはずです.そこで
という写像を決定することが可能なはずです.そこで 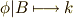 という写像が一意的に決められることになり,この写像によって
という写像が一意的に決められることになり,この写像によって  は適当な有限巡回群
は適当な有限巡回群 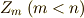 と同型だと言えます.
と同型だと言えます. 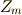 は
は 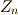 の部分群のはずで,先ほどと同様にして
の部分群のはずで,先ほどと同様にして  も可解群だと言えます.いま,
も可解群だと言えます.いま, 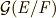 と
と  が可解群なので, 可解群について補足 で示した定理により,
が可解群なので, 可解群について補足 で示した定理により, 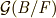 も可解群だと言うこと分かります.■
も可解群だと言うこと分かります.■
定理の証明が長くなったので,ひとまず一休みしましょう.ここまでに,方程式 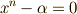 の解に関して,ガロア拡大と可解群の関係を見てきました.ガロア拡大体の列(
の解に関して,ガロア拡大と可解群の関係を見てきました.ガロア拡大体の列( 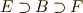 )と,ガロア群の列
)と,ガロア群の列  という二つの話が反変的に対応しているという点をもう一度確認して下さい.
という二つの話が反変的に対応しているという点をもう一度確認して下さい.
| [†] | 拡大体の列と部分群の列は,普通は別の話なわけですが,ガロア理論によって,この両者の間に美しい関係があることが分かったわけです.ここでは,ガロア拡大の話と可解群の話が結びつきました.別々に作っていた部品が,最後に次々と組み合わさって美しい一つの芸術作品を作っていくような趣があります.あと少し定理の証明が続きますが,一つ一つの定理が各部品の連結の役割を果たしています.ガロア理論という芸術品を眺めるために,もう少し大事な定理を見ていきましょう. |
| [‡] | 方程式 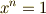 は, は, 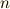 が五次以上でも が五次以上でも 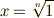 として簡単に代数的に解けることが明らかですから,ガロア群が可解群になるのは当然だと言えます.ちょっとした発展版の として簡単に代数的に解けることが明らかですから,ガロア群が可解群になるのは当然だと言えます.ちょっとした発展版の 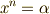 も, も, 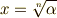 という解が簡単に求められますので,ガロア群が可解群になって当然です.このあと,一般の という解が簡単に求められますので,ガロア群が可解群になって当然です.このあと,一般の 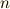 次方程式の可解性を論じるときも, 次方程式の可解性を論じるときも, 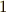 の の 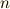 乗根の話が土台として何度も出てきますので,この定理の結果は大事な基礎になります. 乗根の話が土台として何度も出てきますので,この定理の結果は大事な基礎になります. |