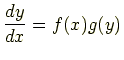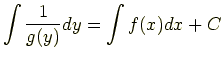変数分離形
微分方程式を変数分離形と呼び,微分方程式のなかで一番基本となるものである. これを解くにはまず,左辺,右辺を同じ変数だけにまとめる. 式(6.1)の場合では左辺に変数が
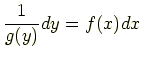 |
(6.2) |
このように変数をイコールをはさんで分離するのだ. そして両辺を積分する.
ここで
例
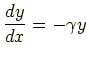 |
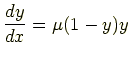 |
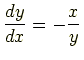 |
注意: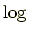 の積分について
の積分について
不定積分
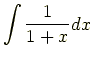 の解は
の解は
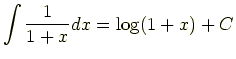 というふうに絶対値なしの値になる.
したがって微分方程式を解くときにでてくる
というふうに絶対値なしの値になる.
したがって微分方程式を解くときにでてくる
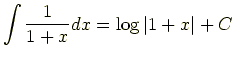 |
という種類の計算は
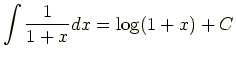 |
と簡略化することができ,絶対値のことを気にしなくてもいい.
物理のかぎプロジェクト / 平成19年1月14日