テンソル成分の加法と乗法
テンソル同士の基本的な計算を決めることにします.いきなりこのページを読んでいる試験直前の人は,計算規則だけ暗記して下さい.テンソル空間の代数的構造を少し勉強してきた読者の方は,註の意味をしっかり理解できるか確認して下さい.
普通の活字の部分は最低限の基礎ですが,註の内容も問題なく理解できると良いです.
加法
テンソルの足し算は,階数が同じテンソル同士でしか定義できないものとします.階数が同じテンソルが二つあった場合,その個々の成分の和からなるテンソルを,テンソルの和と定義します.ベクトルの加法で,成分同士を足し合わせたのと同じことです.

和は,座標変換の際,もとの二つのテンソルと同じ変換則に従うことが示せます. 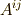 と
と 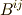 の変換則を
の変換則を 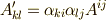 ,
, 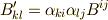 とすると次式がなりたちます.
とすると次式がなりたちます.
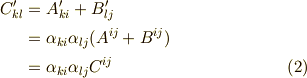
確かに式 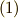 によって定義される和も,階数の等しいテンソルになります.
によって定義される和も,階数の等しいテンソルになります.
| [*] | テンソルの基底を明示的につけて,例えば二階のテンソルを 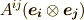 と書けば,式 と書けば,式 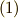 の加法とは,同じ基底の係数同士を足すこと の加法とは,同じ基底の係数同士を足すこと 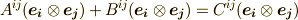 だと分かるでしょう.テンソルの基底もベクトル空間を張っており( テンソルとベクトル空間 参照),一般にベクトル空間の元で基底が同じベクトルの和は,基底は変わらず成分同士を足せば良いことがベクトル空間の定義から示すことが出来ます. だと分かるでしょう.テンソルの基底もベクトル空間を張っており( テンソルとベクトル空間 参照),一般にベクトル空間の元で基底が同じベクトルの和は,基底は変わらず成分同士を足せば良いことがベクトル空間の定義から示すことが出来ます. |
添字の上下による区別
テンソル同士の和は階数が同じテンソルにしか定義できないと書きましたが,テンソルには添字の上下による形の区別があります. 加法は形が同じテンソル同士にしか定義できない ものとします.
以下に,共変テンソル,反変テンソル,混合テンソルの加法を例示します.




混合テンソルで,添字に順番がある場合, 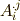 と
と 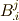 で加法は出来ませんので注意して下さい.
で加法は出来ませんので注意して下さい.
| [†] | この規則も基底を考えれば当然です.例えば 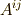 は基底 は基底 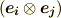 にかかる係数, にかかる係数, 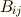 は基底 は基底 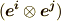 にかかる係数ですが, にかかる係数ですが, 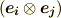 と と 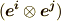 は違うベクトルですから,単純に成分を足し合わせるようなことは出来ないわけです.なぜ,同じ形のテンソル同士にしか和が定義できないのか分かりましたね.また,テンソル積は一般に非可換ですから, は違うベクトルですから,単純に成分を足し合わせるようなことは出来ないわけです.なぜ,同じ形のテンソル同士にしか和が定義できないのか分かりましたね.また,テンソル積は一般に非可換ですから, 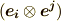 と と 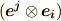 は違います.( 多重線形性とテンソル空間 参照).混合テンソルの添字に順番がある理由は,基底のテンソル積の順番に対応しているわけです. は違います.( 多重線形性とテンソル空間 参照).混合テンソルの添字に順番がある理由は,基底のテンソル積の順番に対応しているわけです. |
| [‡] | テンソル積が可換になるのはどのような場合でしょうか?ここまで順番に記事を読んできた人は,テンソル空間の代数的構造もある程度理解しているはずですから,テンソルの計算規則についてもじっくり考えてみてください. |
| [§] | 成分だけで計算規則を考えると,ベクトル空間の元としてのテンソルの意味が分かりにくくなります.計算規則が覚えやすいこともあって,テンソルとは何かを理解せずに計算規則だけを暗記する人が多いように思います.こんなに面白いのに,残念なことです. |
テンソル積
次式のように,二つの テンソル積 もしくは 外部積 と呼ばれる積を定義します.

つまり,あたかも添字だけ足すようにするわけです.ここでもやはり添字の上下に気をつけなければなりませんが,違う形のテンソルで積を取ることもできます.階数が違うテンソル同士の積でも大丈夫です.加法とは大違いですね.幾つか例を示しましょう.

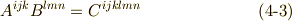

一般にテンソルの積は非可換です.(行列の積が非可換であることを思い出せば,当然ですね.)
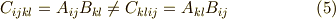
| [¶] | テンソル積では,添字の上下がどのような組み合わせのテンソルに対しても積を考えることが出来ます.これは,どのような基底に対してもテンソル積 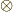 を考えることが出来るからです.例えば式 を考えることが出来るからです.例えば式  は, は, 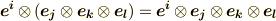 という基底に対応した成分です. という基底に対応した成分です. |
テンソルの縮約規則
同じ添字が上下に分かれて二回出てきたら,その添字について和を取る,という規則がありました.いま三階の混合テンソル 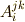 について,添字に同じ文字が出てくる状況を考えてみましょう.
について,添字に同じ文字が出てくる状況を考えてみましょう.
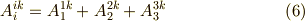
結局,右辺で添字として生き残ったのは 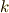 だけですから,これは
だけですから,これは 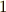 階のテンソル(つまりベクトル)に縮退してしまったと見ることができます.テンソルの定義である変換則を使って,
階のテンソル(つまりベクトル)に縮退してしまったと見ることができます.テンソルの定義である変換則を使って, 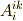 が本当にベクトルなのか,つまりベクトルの変換則を満たすかどうかを確認してみましょう.
が本当にベクトルなのか,つまりベクトルの変換則を満たすかどうかを確認してみましょう.
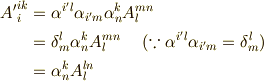
確かに,ベクトルの変換則を満たしています.一般に 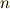 階のテンソルの添字で同じ文字が現われると,その二文字分,テンソルの次元は縮退して
階のテンソルの添字で同じ文字が現われると,その二文字分,テンソルの次元は縮退して  階のテンソルになってしまいます.
階のテンソルになってしまいます.
いま,同じ添字を含むテンソルの外部積を考えてみましょう.
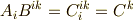
中辺から右辺への変形は,さきほどの結果を使いました.このように,異なるテンソルの積でも同じ添字を含むものは,それだけ次元が縮退します.このような同じ添字を上下に含むテンソル同士の積を 内積 と呼びます.上下に分かれて出現する添字は消えてしまうので,本当にテンソルの階数を示す添字ではありません.その意味で,このような添字を ダミー と呼びます.
| [#] | 縮約規則の復習になりますが,上に二つ,下に二つなど,同じ側に二回出てくる添字の和を取って良いのは,直交座標系においてのみです.一般の曲線座標系では,上下に分かれて出てくる同じ添字の和だけを取ります.さきほど同じ側に同じ添字が出てくるテンソルの和を取りましたが,直交座標系で考えているとの暗黙の了解に基づいています.実際の計算で使う座標系のほとんどは直交座標系ですので,この点にあまり神経質になることはありませんが,せっかくなのできちんと覚えておきましょう. |
| [♠] | テンソルの縮約は,テンソル積によってベクトル空間 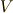 とその双対空間 とその双対空間 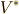 の元はスカラーに写像されるという性質に依拠しています.ベクトルについては, 一般の座標系における内積と外積 で縮約をしても良い理由を説明しましたが,背景にある事情は基本的には同じですが,テンソルの縮約を考えると,ベクトル空間とテンソル積の性質がより一般的で本質的に理解できると思います.この問題は 縮約をもう一度考える で詳しく考察する予定です. の元はスカラーに写像されるという性質に依拠しています.ベクトルについては, 一般の座標系における内積と外積 で縮約をしても良い理由を説明しましたが,背景にある事情は基本的には同じですが,テンソルの縮約を考えると,ベクトル空間とテンソル積の性質がより一般的で本質的に理解できると思います.この問題は 縮約をもう一度考える で詳しく考察する予定です. |