一般の座標系における内積と外積
既に,読者のみなさんは内積と外積という二種類の積をよく知っていると思います.しかし,はじめて内積や外積を勉強したとき,共変ベクトルや反変ベクトルというベクトルの種類をあまり気にしていなかったのではないでしょうか.
この記事では共変ベクトルや反変ベクトルの概念を意識して,もう一度,内積や外積を考え直してみます.
内積
ベクトル  の内積には,
の内積には,  が共変ベクトルか反変ベクトルかによって,添字の上下について次の四通りの組み合わせが考えられるでしょう.
が共変ベクトルか反変ベクトルかによって,添字の上下について次の四通りの組み合わせが考えられるでしょう.
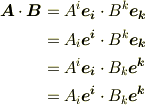
計量テンソルを使えば,上式の各行は次のように書き換えられます.上式と次式は一行ずつ対応しています
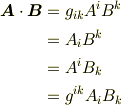
等号で結ばれていますから,どの表現を使っても全く同じ意味なのですが,特にここで興味深いのは,二行目と三行目の表式です.
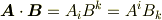
内積はスカラーですから, 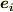 や
や 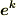 などの基底が関係しないのは当然としても,計量テンソルの成分さえ出てきていません.つまり,基底の取り方が全く問われていないわけで, 添字の上下の異なる二つのベクトルの内積は,座標系の取り方と本当に無関係である ということが主張されているわけです.
などの基底が関係しないのは当然としても,計量テンソルの成分さえ出てきていません.つまり,基底の取り方が全く問われていないわけで, 添字の上下の異なる二つのベクトルの内積は,座標系の取り方と本当に無関係である ということが主張されているわけです.
もちろん,スカラーである内積が,座標系によらない値であるのは当然なのですが,式の表現に座標系の取り方が全く関係しないというのは,計算上,大変に都合のよいことです.
ベクトルの長さは,自分自身との内積の平方根として定義されましたから,添字の上下の異なる表現を使って,次のように書けます.
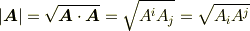
ベクトル  のなす角を
のなす角を 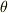 とすれば内積の定義より次式を得ますが,添字の上下の違うベクトルを組み合わせれば,面倒な計量テンソルが出てきませんから座標系の取り方を気にしなくて済み,やはり非常に便利です.
とすれば内積の定義より次式を得ますが,添字の上下の違うベクトルを組み合わせれば,面倒な計量テンソルが出てきませんから座標系の取り方を気にしなくて済み,やはり非常に便利です.
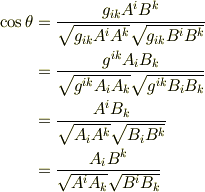
縮約について考えてみる
『添字が上下に分かれていたら,その和を取る』という,アインシュタインの縮約という約束がありました.しかし,本当にいきなり和を取ってしまっても大丈夫なのか,という点を最初にきちんと説明しませんでした.さきほど考えた内積の議論から,和を取ってしまっても良い理由が分かります.
例えば 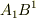 という積は,座標系の取り方による量です.
という積は,座標系の取り方による量です. 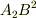 も
も 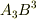 もやはり座標系によります.ところが,この三つの和
もやはり座標系によります.ところが,この三つの和 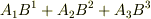 は内積になり,たちまち座標系にはよらない量となります.添字が上下に分かれていれば,面倒な計量因子も出てこないので式の表現そのものが座標系とは独立なスカラーになります.一般に,ベクトルやテンソルの成分は座標系によりますが,添字が上下に分かれた内積は一種の保存量になってしまうわけです.縮約は,各成分
は内積になり,たちまち座標系にはよらない量となります.添字が上下に分かれていれば,面倒な計量因子も出てこないので式の表現そのものが座標系とは独立なスカラーになります.一般に,ベクトルやテンソルの成分は座標系によりますが,添字が上下に分かれた内積は一種の保存量になってしまうわけです.縮約は,各成分 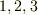 別に三本の式を考える代わりに,それらを足してしまって内積にしてしまえば,座標系によらずにいつでも成り立つ式を作れるという事実に基づいていたのです.(
別に三本の式を考える代わりに,それらを足してしまって内積にしてしまえば,座標系によらずにいつでも成り立つ式を作れるという事実に基づいていたのです.( 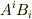 のような項が出てきても,単一の成分だけを考えたいときには『ただし和は取らない』と注釈を加えることがあります.)
のような項が出てきても,単一の成分だけを考えたいときには『ただし和は取らない』と注釈を加えることがあります.)
外積
外積は『ベクトル  ベクトル
ベクトル  ベクトル』という計算でしたが,共変ベクトルと反変ベクトルの組合わせはどのようになるのでしょうか?実は,私たちは 双対基底 で共変基底と反変基底を相互に変換する公式を得ていますので,本質的にこの組み合わせに悩む必要はありません.
ベクトル』という計算でしたが,共変ベクトルと反変ベクトルの組合わせはどのようになるのでしょうか?実は,私たちは 双対基底 で共変基底と反変基底を相互に変換する公式を得ていますので,本質的にこの組み合わせに悩む必要はありません.
また,外積は座標不変量ではありませんから,基底ベクトルの取り方に依存します.つまり,異なる基底に従う異種のベクトルで,そのまま外積を計算することは出来ず,その場合には,予め座標変換をして同じ基底による表現に揃えてやらなければなりません.結局,外積の計算では,同じ基底によるベクトルの計算,つまり『共変ベクトル×共変ベクトル』か『反変ベクトル×反変ベクトル』という組み合わせ以外には意味がありません.
まず,反変ベクトル同士の外積を考えましょう.基底は一般のアフィン基底だとします.定義に従って,次のように計算できます.
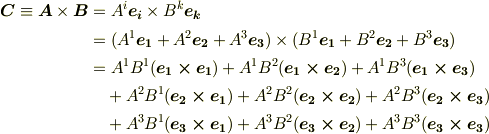
いま,考えている基底は正規直交基底ではありませんから,基底同士の外積 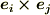 はこれ以上簡単な形に直せません.(
はこれ以上簡単な形に直せません.(  と出来るのは正規直交基底の場合に限ります.)しかし,次の双対基底の変換公式を使えば,もう少し式を簡単にできます.
と出来るのは正規直交基底の場合に限ります.)しかし,次の双対基底の変換公式を使えば,もう少し式を簡単にできます.
![\bm{e_{j}} \times \bm{e_{k}} &= [\bm{e_{i}} \cdot (\bm{e_{j}} \times \bm{e_{k}}) ]\bm{e^{i}} \\&= V \bm{e^{i}}](./9e941fbb7eb38cb43bc91b6405aab475.png)
式中 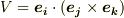 と置きました.
と置きました.  は
は  の張る平行六面体の体積で,もちろんスカラー量です.この関係を使うと,外積の表現は次のように簡単化されます.
の張る平行六面体の体積で,もちろんスカラー量です.この関係を使うと,外積の表現は次のように簡単化されます.
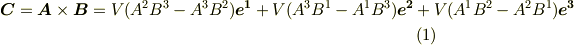
左辺を 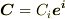 と置き,両辺を比べれば成分だけの表式を得ます.
と置き,両辺を比べれば成分だけの表式を得ます. 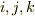 は巡回的な添字だとします.
は巡回的な添字だとします.
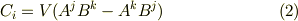
これが,外積を反変基底  を使って表現したときの成分です.式
を使って表現したときの成分です.式 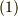 で双対基底の変換公式を
で双対基底の変換公式を 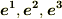 に対して再び用いれば,共変基底による表現も得ます.
に対して再び用いれば,共変基底による表現も得ます.
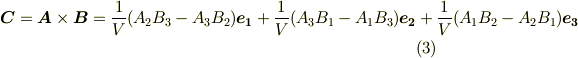
左辺を 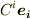 と置いて両辺を比べれば,成分の式を得ます.
と置いて両辺を比べれば,成分の式を得ます.
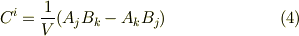
みなさんが最初に習った外積には,恐らく 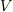 や
や  はついていなかったと思いますが,それは長さ
はついていなかったと思いますが,それは長さ 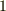 の単位ベクトルを基底とした直交座標系では常に
の単位ベクトルを基底とした直交座標系では常に  となるからです.上の二つの表式は斜交座標系にも対応した,より一般的な外積の表式になっています.
となるからです.上の二つの表式は斜交座標系にも対応した,より一般的な外積の表式になっています.
| [*] | ここで出てきた 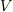 は計量テンソルの行列式の平方根 は計量テンソルの行列式の平方根 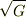 にも等しいのでした.( 計量テンソル を復習してください.)一般のアフィン基底で外積を計算すると, にも等しいのでした.( 計量テンソル を復習してください.)一般のアフィン基底で外積を計算すると, 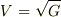 のようなものが前についてきます.これは一種の比例定数で,スカラー密度と呼ばれることもあります.デカルト座標系のスカラー密度は のようなものが前についてきます.これは一種の比例定数で,スカラー密度と呼ばれることもあります.デカルト座標系のスカラー密度は 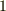 です. です. |