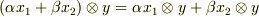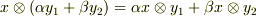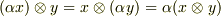テンソルとベクトル空間
双線形関数の全体がベクトル空間 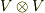 を張ることを見ましたが( 双線形関数 参照),この記事では,そのベクトル関数の元がどのようなものなのかを考えます.(←実は二階のテンソルです^^.)
を張ることを見ましたが( 双線形関数 参照),この記事では,そのベクトル関数の元がどのようなものなのかを考えます.(←実は二階のテンソルです^^.) 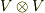 を 双線形空間 と呼びます.
を 双線形空間 と呼びます.
双線形空間(その1)
新しく 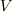 のテンソル積から作ったベクトル空間
のテンソル積から作ったベクトル空間 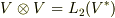 というものを考えましたが,具体的に
というものを考えましたが,具体的に 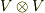 の元はどのようなものなのでしょうか.
の元はどのようなものなのでしょうか. 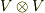 の元は,
の元は, 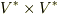 の元に双線形汎関数として作用するわけですが,具体的な作用の仕方として,次の形を考えると,うまく双線形性を満たすことが示せます.式中,
の元に双線形汎関数として作用するわけですが,具体的な作用の仕方として,次の形を考えると,うまく双線形性を満たすことが示せます.式中, 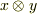 は
は 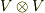 の元,
の元, 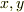 は
は 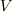 の元,
の元, 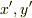 は
は 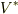 の元で,
の元で,  は
は 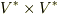 の元だとします.
の元だとします.
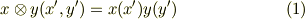
左辺は少し見にくいですが, 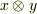 が関数の名前,
が関数の名前,  が変数だと見てください.右辺は,
が変数だと見てください.右辺は, 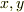 を
を 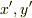 に対する線形汎関数と見て,ベクトル値関数のように表現しています.
に対する線形汎関数と見て,ベクトル値関数のように表現しています.
| [*] | 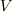 と と 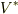 の基底として,双対基底 の基底として,双対基底 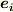 と と 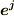 を考えれば, を考えれば, 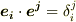 より, より,  の の 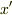 に対する作用(もしくは に対する作用(もしくは 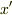 の の  に対する作用)は一つの成分を抜き出す働きになります.( 双対基底 参照.)このとき,式 に対する作用)は一つの成分を抜き出す働きになります.( 双対基底 参照.)このとき,式 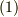 の右辺は の右辺は 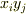 のような成分の積で書けるでしょう. のような成分の積で書けるでしょう. 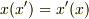 ですので,式 ですので,式 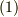 の右辺を の右辺を  と書いても同じことです.この辺りが不安な人は,もう一度 双対空間 , 双対基底と双対空間 を復習して下さい. と書いても同じことです.この辺りが不安な人は,もう一度 双対空間 , 双対基底と双対空間 を復習して下さい. |
式 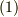 で定義された作用が,双線形性を持つことを確認してみましょう.定義式
で定義された作用が,双線形性を持つことを確認してみましょう.定義式 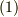 を使って式変形していきます.
を使って式変形していきます.
【双線形性】
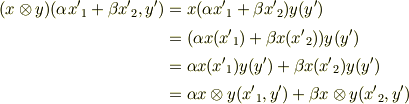
確かに双線形性を満たしますね.また,次のような算法を満たすことも示せます.(証明はどれも簡単なので省略します.双線形を示したのと同じように式変形していけば,左辺から右辺を導くのは簡単です.)
【 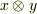 が満たす性質】
が満たす性質】
式 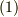 のように定義したテンソル積
のように定義したテンソル積 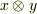 は双線形性を持ち,
は双線形性を持ち, 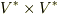 の元に対して双線形関数として働きますので,
の元に対して双線形関数として働きますので, 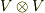 の元であると言えます.
の元であると言えます.
Important
関数 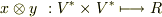 の作用を
の作用を 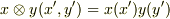 と定めると,
と定めると, 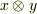 は
は 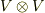 の元になります.
の元になります.
双線形空間(その2)
前セクションで確認したのは十分条件ともいうべきものですが,逆に 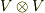 の元は全てスカラー係数
の元は全てスカラー係数 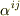 をつけて,
をつけて, 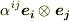 の形で一意的に表現できることが示せます.ただし
の形で一意的に表現できることが示せます.ただし  を
を 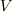 の基底の一つとします.
の基底の一つとします.
theorem
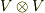 の元は,一意的に
の元は,一意的に 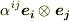 の形に表現することが出来ます.
の形に表現することが出来ます.
proof
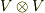 の任意の元(
の任意の元(  とします)を取ります.
とします)を取ります.  は双線形汎関数ですので,
は双線形汎関数ですので, 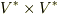 の元をある実数に移します.そこで
の元をある実数に移します.そこで 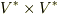 の基底を
の基底を 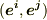 とすると,
とすると, 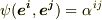 を満たす
を満たす 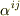 が存在するはずです.一方,ある
が存在するはずです.一方,ある 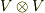 の元
の元 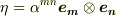 を
を 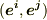 に作用させると,式
に作用させると,式 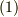 より
より 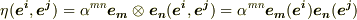 となります.ここで双対基底の性質を使うと
となります.ここで双対基底の性質を使うと 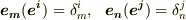 ですから,結局
ですから,結局 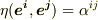 を得ます.
を得ます. 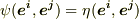 となったわけですが,各
となったわけですが,各 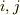 についてこの等式は成り立ちますから,
についてこの等式は成り立ちますから, 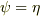 が言えます.すなわち,
が言えます.すなわち, 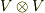 の元で同じ作用をする元は同一の元だと見なせるわけで,これは
の元で同じ作用をする元は同一の元だと見なせるわけで,これは 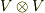 の表現が一意的だということです.■
の表現が一意的だということです.■
今までも,二階のテンソルは 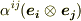 の形に書け,
の形に書け,  がテンソル成分,
がテンソル成分, 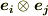 が基底だという説明を何度かしてきました.( もう一度だけ内積外積 , テンソルの概念 , ベクトルからテンソルを作る 等参照.)しかし『基底』という言葉は,ベクトルの表現からの類推で使っていたに過ぎず,本当に
が基底だという説明を何度かしてきました.( もう一度だけ内積外積 , テンソルの概念 , ベクトルからテンソルを作る 等参照.)しかし『基底』という言葉は,ベクトルの表現からの類推で使っていたに過ぎず,本当に 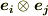 が何かベクトル空間の基底になっているのかという点は誤魔化していました(^_^ ;). ようやくここに至って,確かに
が何かベクトル空間の基底になっているのかという点は誤魔化していました(^_^ ;). ようやくここに至って,確かに 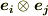 が
が  というベクトル空間の基底であり,また
というベクトル空間の基底であり,また  の元は双線形性という性質を持つことを確認できました.
の元は双線形性という性質を持つことを確認できました.
既に察しがついているかと思いますが,ここで用いた  という記号は,さらに高次のベクトル空間にまで拡張できます.
という記号は,さらに高次のベクトル空間にまで拡張できます.
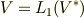
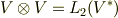
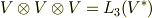

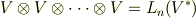
いきなり一般化してしまいましたが,  に出てくるのは,線形性を
に出てくるのは,線形性を  変数関数にまで拡張した,いわば
変数関数にまで拡張した,いわば  重線形関数です.一般に,多変数関数の個々の変数に対して働く高次の線形性を 多重線形性 と呼びます.この意味で,線形関数は一重線形関数,双線形関数は二重線形関数と呼んでも良く,いままで考えてきたベクトル空間
重線形関数です.一般に,多変数関数の個々の変数に対して働く高次の線形性を 多重線形性 と呼びます.この意味で,線形関数は一重線形関数,双線形関数は二重線形関数と呼んでも良く,いままで考えてきたベクトル空間 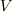 や,双線形空間
や,双線形空間 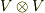 も,多重線形空間の特別な場合に過ぎなかったと見ることが出来ます.ただし,普通は多重線形関数の作るベクトル空間を多重線形空間とは呼ばずに, テンソル空間 と呼びます.
も,多重線形空間の特別な場合に過ぎなかったと見ることが出来ます.ただし,普通は多重線形関数の作るベクトル空間を多重線形空間とは呼ばずに, テンソル空間 と呼びます.
だんだんテンソルの世界が展望できてきましたか?代数的な視点からテンソルの構造を考察してみましたが,テンソルの意味がかなりはっきりして来たと思います.どうやら『多重線形性』という性質がテンソルの代数的構造ではキーワードのようですね.
| [†] |  という記号はなかなか良くできています. という記号はなかなか良くできています.  を関数のように見て『 を関数のように見て『 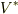 から,多重線形性を使って新しいベクトル空間を作る』と読むこともできます. から,多重線形性を使って新しいベクトル空間を作る』と読むこともできます. 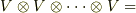 のように書いていただけでは何個掛けたかが分かりにくいので, のように書いていただけでは何個掛けたかが分かりにくいので,  と書くと便利ですが, と書くと便利ですが, 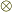 の冪乗の形で の冪乗の形で 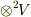 , , 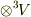 ,..., ,...,  のように書く書き方もあります. のように書く書き方もあります. |