グリーン関数を理解しよう(ファインマンダイアグラム)
これからいくつかの記事を通して,
物性物理で扱われる絶対零度におけるグリーン関数の理解を目指します.
いくつかの定理などの証明は省略して,要点の俯瞰をする方針で行きます.
参考文献として,下に書くMahan先生の本を挙げて
おきます.このシリーズでは 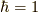 とします.
前の記事は ウィックの定理 です.
次の記事は ダイソン方程式と自己エネルギー です.( 目次 )
とします.
前の記事は ウィックの定理 です.
次の記事は ダイソン方程式と自己エネルギー です.( 目次 )
基本的対応
この記事ではファインマンダイアグラムを学びます. まず, 前回 の最後の式を思い出しましょう. 再掲すると,
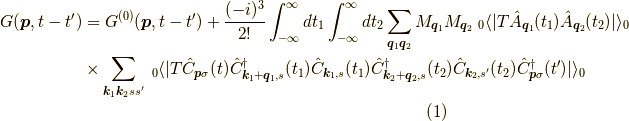
という,相互作用のあるグリーン関数の自由なグリーン関数の展開の電子部分で,
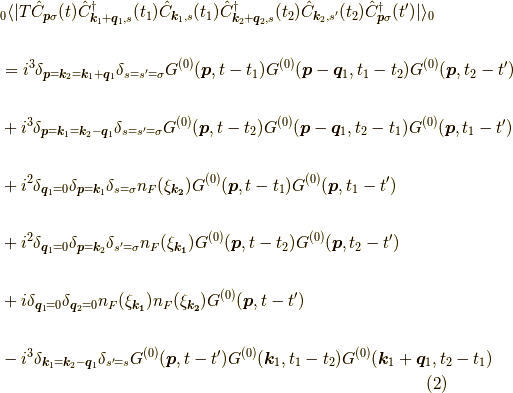
というものです.ここにさらにフォノンの自由グリーン関数がかかっています.
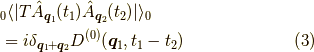
今回はこの式  をダイアグラムで表すことをします.
それは,粒子の振る舞いを下図の様に対応させる手法です.
をダイアグラムで表すことをします.
それは,粒子の振る舞いを下図の様に対応させる手法です.
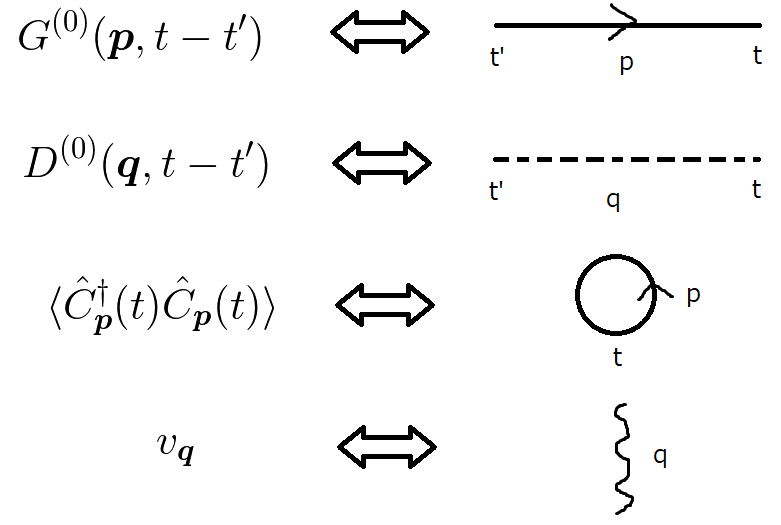
一番上の実線は自由な電子グリーン関数です. 矢印が時間の流れ(左から右)へ付いているのは電子, 逆行しているのは反粒子である陽電子です.
二番目の点線は自由なフォノングリーン関数です.
この  に矢印は付けません.
というのは,,
に矢印は付けません.
というのは,,
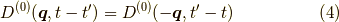
と書けるので, 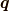 の符号は本質でないからです.
の符号は本質でないからです.
三番目は電子線のループです.
同時刻の真空期待値  が
粒子数演算子であることと関係があることが言えるはずですが,
どうしてループと粒子数が関係するのか私は知りません.
が
粒子数演算子であることと関係があることが言えるはずですが,
どうしてループと粒子数が関係するのか私は知りません.
最後はクーロン反発です. 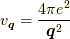 のことですね.これはこの話においては同時刻に放出と吸収が起こるとしています.
力が瞬間に伝わるという近似です.
のことですね.これはこの話においては同時刻に放出と吸収が起こるとしています.
力が瞬間に伝わるという近似です.
なお,必ずしも  ではありません.
ではありません.  の時は
時間を粒子が逆行する反粒子だと考えます.
の時は
時間を粒子が逆行する反粒子だと考えます.
個々のダイアグラム対応
以上を式 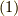 に対応させた図を載せていきます.
に対応させた図を載せていきます.
図1(a).

図1(b)
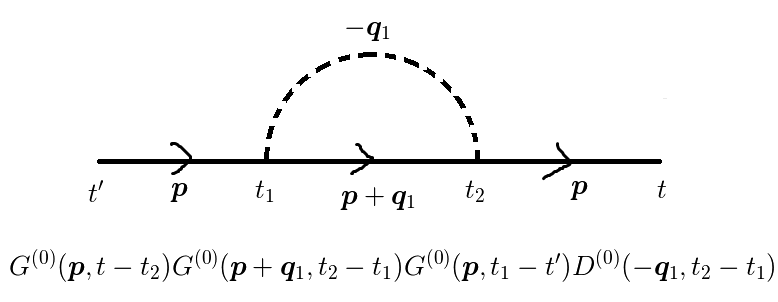
図1(c)
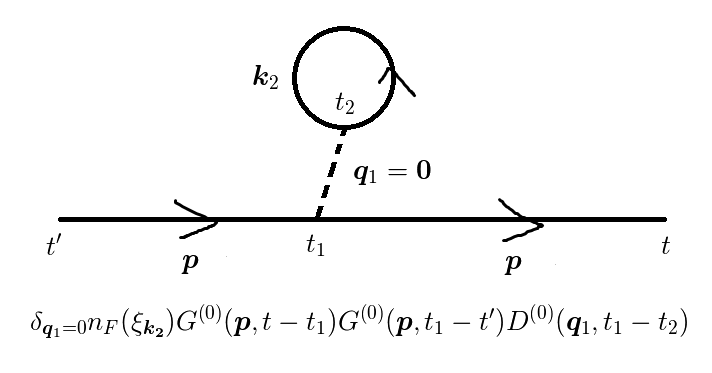
図1(d)
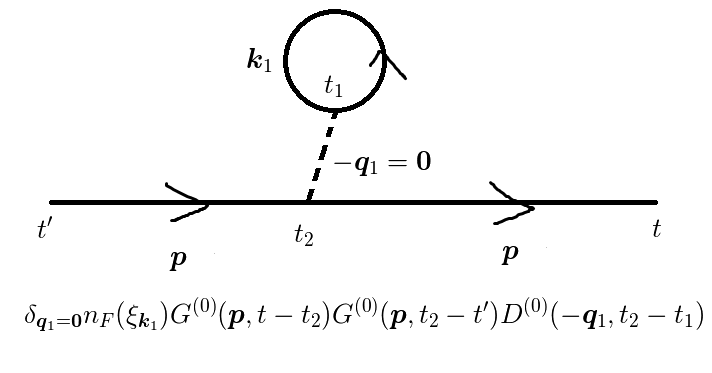
図1(e)
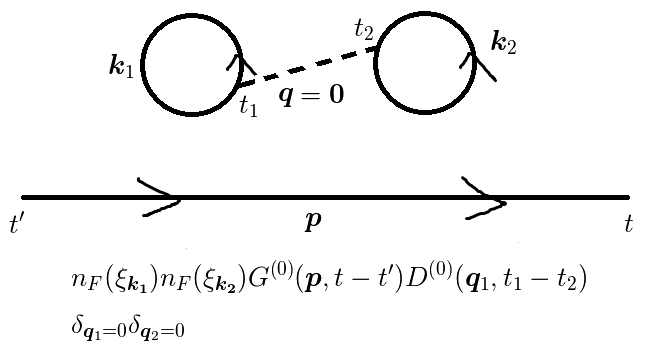
図1(f)
さて,図(c),(d),(e)では波数ゼロのフォノンが出てきます.
しかし,  のフォノンは存在しません.
よって,この項からの寄与はゼロと考えます.
しいていえば,結晶の並進や恒久的なストレスのことですが,
ハミルトニアンには関係しません.
よって, 前回 の電子-フォノン相互作用の式
のフォノンは存在しません.
よって,この項からの寄与はゼロと考えます.
しいていえば,結晶の並進や恒久的なストレスのことですが,
ハミルトニアンには関係しません.
よって, 前回 の電子-フォノン相互作用の式  の
和からは,
の
和からは,  は除かれるべきだそうです.
その和とは再掲しておくと,
は除かれるべきだそうです.
その和とは再掲しておくと,
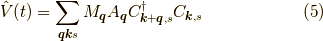
のことです.
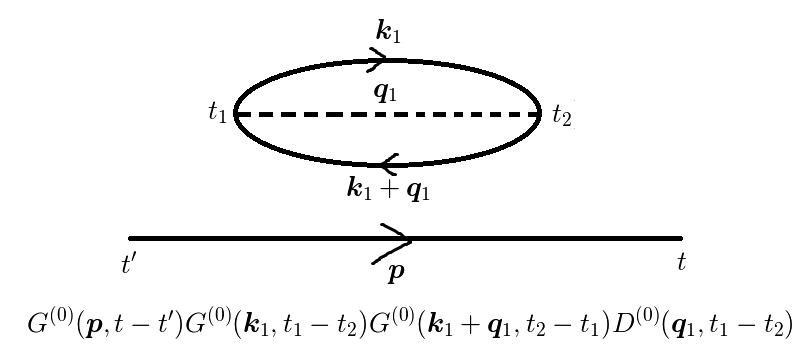
図(a),(b)はまとめて考えると,
![\dfrac{1}{2!} &\int_{-\infty}^\infty dt_1 \int_{-\infty}^\infty dt_2 \sum_{\bm{q}} |M_{\bm{q}}|^2 D^{(0)}(\bm{q},t_1-t_2) \\&\times[G^{(0)}(\bm{p},t-t_1)G^{(0)}(\bm{p}-\bm{q},t_1-t_2)G^{(0)}(\bm{p},t_2-t^\prime) \\&+G^{(0)}(\bm{p},t-t_2)G^{(0)}(\bm{p}+\bm{q},t_2-t_1)G^{(0)}(\bm{p},t_1-t^\prime) ]\tag{6}](./e24889e72b75b3d765103f2de76e19d6.png)
今,この二つの項はパラメータ 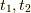 の入れ替えで移り変わります.
の入れ替えで移り変わります. 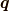 の符号は
の符号は
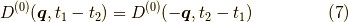
を考えると,全く同じ寄与だと分かります.
つまり,この前の因子 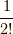 が
が 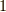 に変わります.
に変わります.
図(f)は,

という寄与になります.ここで, 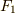 は
は
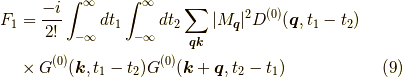
という(無限大の)定数因子です.
真空偏極項とキャンセル定理
この図(f)の様につながっていないグラフを非連結グラフと言います.
そして, 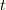 か
か 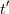 とつながっている電子線が外線といいます.
その閉じたループで外線とつながっていない部分をバブルと言います.
もっと高次の非連結グラフ
とつながっている電子線が外線といいます.
その閉じたループで外線とつながっていない部分をバブルと言います.
もっと高次の非連結グラフ 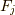 もあります.それらもやはり定数を掛け算する寄与になります.
それらをトータルしたものを
もあります.それらもやはり定数を掛け算する寄与になります.
それらをトータルしたものを  とします.ゼロ次の自由なグリーン関数そのものの寄与
とします.ゼロ次の自由なグリーン関数そのものの寄与 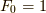 として,
として,

となります.ここでウィックの定理を思い出しましょう.
相互作用のあるグリーン関数とその分母 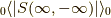 を比較してみます.
を比較してみます.
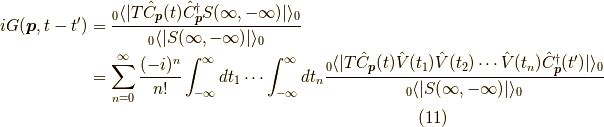
と,
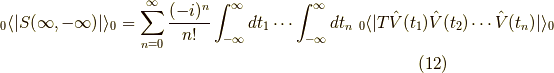
です.この  の内容を考えると
の内容を考えると  に等しいことが分かります.外線の無い(足の無い)相互作用のあるグリーン関数と言えば分かるでしょうか.
よくよく考えてみると,グリーン関数の内で
に等しいことが分かります.外線の無い(足の無い)相互作用のあるグリーン関数と言えば分かるでしょうか.
よくよく考えてみると,グリーン関数の内で  を含むものと
を含むものと 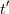 を含むものは必ずつながっています.なぜなら,電子線に分岐や行き止まりはないからです.すると,残りの部分はバブルになっていると分かります.相互作用のあるグリーン関数
を含むものは必ずつながっています.なぜなら,電子線に分岐や行き止まりはないからです.すると,残りの部分はバブルになっていると分かります.相互作用のあるグリーン関数 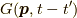 の内で,バブルが無く,かつ,ありうる全てのつながり方を持っている関数を考え,これを連結グリーン関数
の内で,バブルが無く,かつ,ありうる全てのつながり方を持っている関数を考え,これを連結グリーン関数 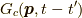 とします.またここで,
とします.またここで,  は全てのバブルの寄与でした.
は全てのバブルの寄与でした.
図2
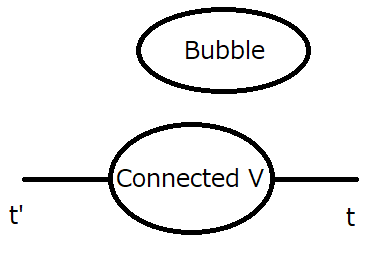
すると,これは図2を見ると,

つまり,
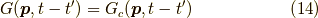
がいえることになります.はて,何が嬉しいの?と仰る方もいるかもしれません.いえいえ,
これは凄いことです.同じ結果を得るのに,連結なものだけを考えることで良い.と言う事になったからです.
こうして,相互作用のあるグリーン関数 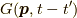 の計算は大幅に簡略化されたことになります.
の計算は大幅に簡略化されたことになります.
トポロジー的分類
先ほど図(a),(b)は等しい事が言えましたね.
同様に  次の連結な摂動はパラメータの置き換えが
次の連結な摂動はパラメータの置き換えが  通りあります.
通りあります.
つまり,
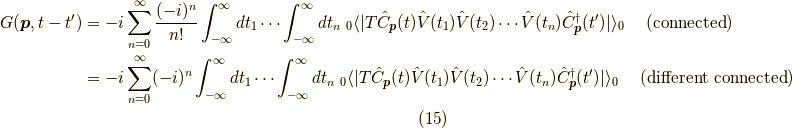
これもまた計算の手間を簡略化してくれることです.
今日はここまで,お疲れ様でした.
次の記事は ダイソン方程式と自己エネルギー です.