グリーン関数を理解しよう(ダイソン方程式と自己エネルギー)
これからいくつかの記事を通して,
物性物理で扱われる絶対零度におけるグリーン関数の理解を目指します.
いくつかの定理などの証明は省略して,要点の俯瞰をする方針で行きます.
参考文献として,下に書くMahan先生の本を挙げて
おきます.このシリーズでは  とします.
前の記事は ファインマンダイアグラム です.
次の記事は フォトンのグリーン関数 です.( 目次 )
とします.
前の記事は ファインマンダイアグラム です.
次の記事は フォトンのグリーン関数 です.( 目次 )
自己エネルギー
グリーン関数の通常のフーリエ変換を
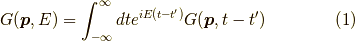
とすると,自由なグリーン関数のフーリエ変換は 空バンドの場合は
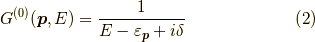
縮退した電子ガスの場合は

でした.
さて,電子はその位置を移動して時間発展する時に,
自分自身と様々な相互作用を常にしています.
相互作用がない時が自由なグリーン関数なのです.
その相互作用を考慮したグリーン関数 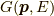 を
自由なグリーン関数
を
自由なグリーン関数 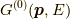 と
自己エネルギー
と
自己エネルギー 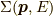 のシンプルな式で表せる.
という事を示すのがこの記事の目的です.
自己エネルギーは摂動論的アプローチで無限次まで足すことで
求められます.主要部分が低次から数項で良い近似になっているときは良いのですが,
悪い時はアプローチ方法を変えなければなりません.
のシンプルな式で表せる.
という事を示すのがこの記事の目的です.
自己エネルギーは摂動論的アプローチで無限次まで足すことで
求められます.主要部分が低次から数項で良い近似になっているときは良いのですが,
悪い時はアプローチ方法を変えなければなりません.
表したい 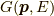 を確認しておきましょう.
を確認しておきましょう.
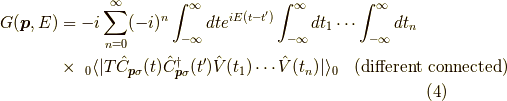
自由なグリーン関数で表した二次の項までの展開は,
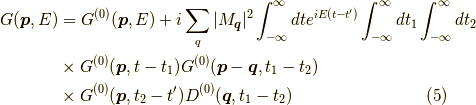
ここで, 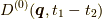 に逆フーリエ変換を用います.
に逆フーリエ変換を用います.
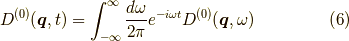
よって,
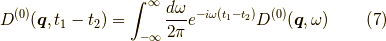
だから,
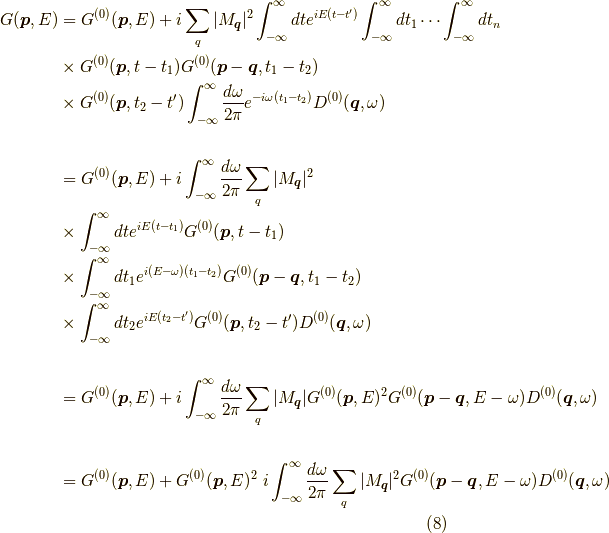
ここで,
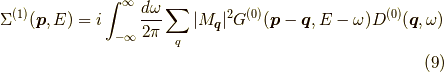
であり,これを1フォノン過程の自己エネルギーと言います.数式的には,外線の無いグリーン関数であり,自己との相互作用部分と言えるでしょう.
図1
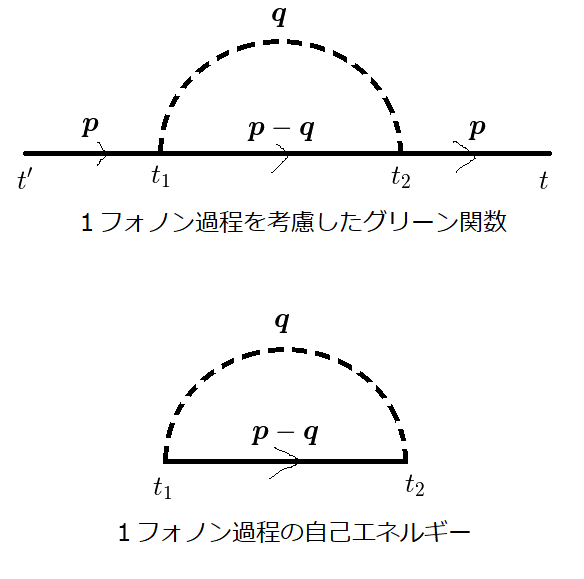
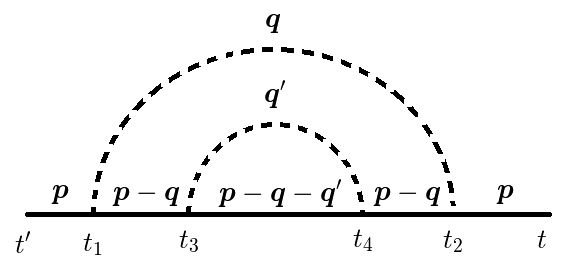
次の摂動項である2フォノン過程の自己エネルギーを示すと,
図2(a)
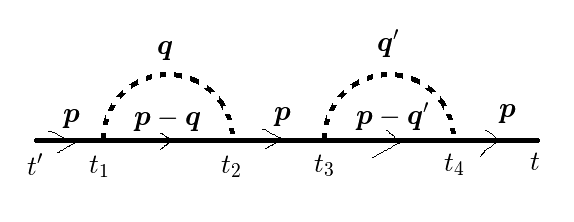
これは,
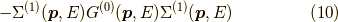
です.
図2(b)
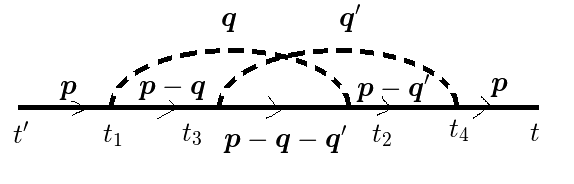
は,

であり,
図2(c)
は,
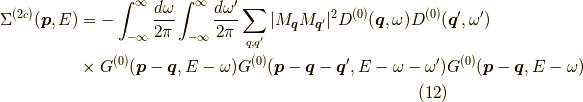
となります.
図2(d)

ここで,時間に逆行している(左から右に時間は流れる)電子線がありますが,これはホールもしくは陽電子です.
つまり,  で起こった電子と陽電子が対生成と
で起こった電子と陽電子が対生成と 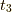 で対消滅をし,
それが外線電子に影響を及ぼすと言う事です.
で対消滅をし,
それが外線電子に影響を及ぼすと言う事です.
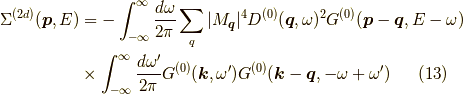
同時刻での電子,フォノン,陽電子の運動量和(反粒子はマイナス倍を足す)は常に一定であることを注意してください.
(式 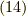 では
では 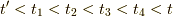 としています.)
としています.)
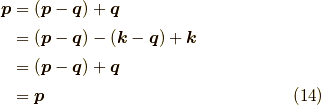
ここまでの近似で 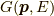 を表すと,
を表すと,
![G(\bm{p},E) = G^{(0)}\left( 1 + G^{(0)}[ \Sigma^{(1)} + \Sigma^{(2b)} + \Sigma^{(2c)} + \Sigma^{(2d)}]+[G^{(0)} \Sigma^{(1)}]^2 + \cdots \right)\tag{15}](./778561d6b8b5dae1396314c9830b558d.png)
これを続けていくと,自己エネルギーは

となります.
ダイソン方程式
ここで,テイラー展開
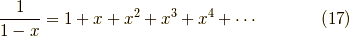
を利用すると,無限回の相互作用の繰り返しを挿入した式が  なので,
なので,
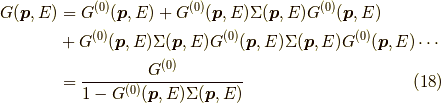
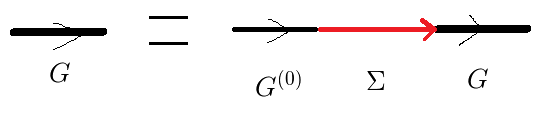
となります.これがダイソン方程式です.

とも書きます.(下図参照)
1.空バンドでのグリーン関数
この時,
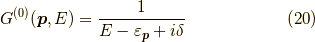
であり,
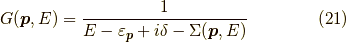
です.
2.縮退電子ガス(金属中)でのグリーン関数
この時,
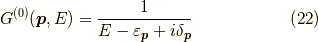
であり,
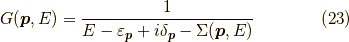
です.グリーン関数の虚部と自己エネルギーの虚部は 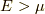 か
か 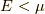 かによって,符号を変えます.
かによって,符号を変えます.
3.フォノングリーン関数
この時,ダイソン方程式は,
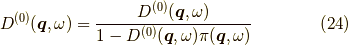
であり,
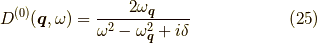
でしたから,
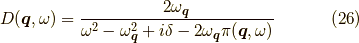
となるようです.私にはフォノン同士の相互作用がどんなものかは,よく分かりませんでした.
今日はここまで,お疲れ様でした.
次の記事は フォトンのグリーン関数 です.