グリーン関数を理解しよう(ウィックの定理)
これからいくつかの記事を通して,
物性物理で扱われる絶対零度におけるグリーン関数の理解を目指します.
いくつかの定理などの証明は省略して,要点の俯瞰をする方針で行きます.
参考文献として,下に書くMahan先生の本を挙げて
おきます.このシリーズでは 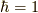 とします.
前の記事は 電子とフォノンのグリーン関数 です.
次の記事は ファインマンダイアグラム です.( 目次 )
とします.
前の記事は 電子とフォノンのグリーン関数 です.
次の記事は ファインマンダイアグラム です.( 目次 )
ちょっと休憩
相互作用 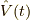 にはどんなものがあるのか,
ここで気晴らしもかねて,三つほど挙げてみようと思います.
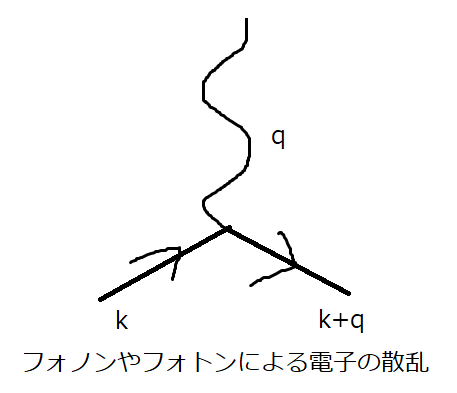
図において時間は左から右に流れます.
にはどんなものがあるのか,
ここで気晴らしもかねて,三つほど挙げてみようと思います.
図において時間は左から右に流れます.
1.電子-電子相互作用
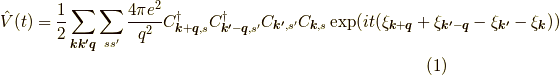
注意として,時間依存性は全て指数関数にまとめられ, 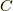 には時間依存性がありません.
には時間依存性がありません.

2.電子-フォノン相互作用
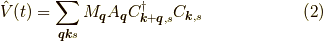
ここで, 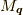 は
は 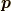 に依存する係数です.
に依存する係数です.
3.電子-フォトン相互作用
これについては,全ハミルトニアンを書きます.
![H = \sum_{i} \dfrac{1}{2m} \left[ \bm{p}_i - \dfrac{e}{c}\bm{A}_i \right]^2 + \sum_{i \neq j} \dfrac{e_i e_j}{2r_{ij}} + \sum_{\bm{k} \lambda} \omega_{\bm{k} \lambda} a^\dagger_{\bm{k} \lambda} a_{\bm{k} \lambda} \tag{3}](./8435e6d1fef6252092b58c883aeefa66.png)
ここで, 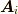 はベクトルポテンシャルで,
はベクトルポテンシャルで, 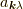 は光子の消滅演算子でありボゾン演算子です.
実はクーロン反発である1は,この3の相互作用として含まれているそうです.
は光子の消滅演算子でありボゾン演算子です.
実はクーロン反発である1は,この3の相互作用として含まれているそうです.
電子のようなフェルミオンは相互作用で粒子数が保存(陽電子はマイナス一個と数える)のに対し,
フォノンの様なボゾンはフェルミオンへ吸収・放出されます.よって,式  の様な
相互作用になるわけです.フォトンもボゾンであるのでフォノンと同じはずですが,
私は式
の様な
相互作用になるわけです.フォトンもボゾンであるのでフォノンと同じはずですが,
私は式 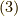 をどう見ていいか分かりません.
をどう見ていいか分かりません.
グリーン関数の展開
グリーン関数を徐々に変形していきます.
それには 相関関数の計算 の式 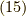 で導出した式を使います.
再掲しておきます.
で導出した式を使います.
再掲しておきます.
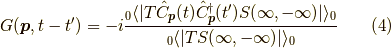
これともう一つ, 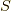 行列の展開式( 相互作用表示とS行列 の式
行列の展開式( 相互作用表示とS行列 の式 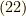 )が必要です.
)が必要です.
![S(t,t^\prime) = T \exp \left[ -i \int_{t^\prime}^t dt_1 \hat{V}(t_1) \right]\tag{5}](./673644d7ee39f168deafc45df39922c3.png)
これを
![S(\infty, -\infty) = T \exp \left[ -i \int_{-\infty}^\infty dt_1 \hat{V}(t_1) \right]\tag{6}](./57621675afc666316c9ef1c7201191dc.png)
とします.式 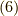 を式
を式 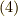 に代入すると,
に代入すると,
![G(\bm{p},t-t^\prime) &= -i \dfrac{_0 \langle | T \hat{C}_{\bm{p}}(t) \hat{C}^\dagger_{\bm{p}}(t^\prime) \exp \left[ -i \int_{-\infty}^\infty dt_1 \hat{V}(t_1) \right] | \rangle_0}{_0 \langle | S(\infty,-\infty) | \rangle_0} \\&= -i \dfrac{_0 \langle | T \hat{C}_{\bm{p}}(t) \hat{C}^\dagger_{\bm{p}}(t^\prime) \sum_{n=0}^\infty \dfrac{(-i)^{n}}{n!} \int_{-\infty}^\infty dt_1 \cdots \int_{-\infty}^\infty dt_n \hat{V}(t_1) \hat{V}(t_2) \cdots \hat{V}(t_n) | \rangle_0}{_0 \langle | S(\infty,-\infty) | \rangle_0} \\&= \sum_{n=0}^\infty \dfrac{(-i)^{n+1}}{n!} \int_{-\infty}^\infty dt_1 \cdots \int_{-\infty}^\infty dt_n \dfrac{_0 \langle | T \hat{C}_{\bm{p}}(t) \hat{C}^\dagger_{\bm{p}}(t^\prime) \hat{V}(t_1) \hat{V}(t_2) \cdots \hat{V}(t_n) | \rangle_0}{_0 \langle | S(\infty,-\infty) | \rangle_0} \\&= \sum_{n=0}^\infty \dfrac{(-i)^{n+1}}{n!} \int_{-\infty}^\infty dt_1 \cdots \int_{-\infty}^\infty dt_n \dfrac{_0 \langle | T \hat{C}_{\bm{p}}(t) \hat{V}(t_1) \hat{V}(t_2) \cdots \hat{V}(t_n) \hat{C}^\dagger_{\bm{p}}(t^\prime) | \rangle_0}{_0 \langle | S(\infty,-\infty) | \rangle_0}\tag{7}](./af564870b7c38a6abc6e8aeaf6ba7c22.png)
となります.何度か言っていますが,こうやってシンプルに書けるのは時間順序積の強みです.時間順序は計算時にしっかり並び順を設定することが必要ですが,表記としては適当に並び方を変えても許されるのです.ですが,書けるだけで全く計算の手間は減っていないのです.なお,最後に変形で時間順序積内でもフェルミオンの演算子の交換の際には符号が変化しなければなりませんが, 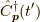 を符号変化なしで最後に持って行けたのは,
を符号変化なしで最後に持って行けたのは, 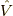 が偶数個の演算子を含んでいるからだと思います.
が偶数個の演算子を含んでいるからだと思います.
ここで 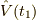 をこの記事の最初に出した電子-電子相互作用にします.
をこの記事の最初に出した電子-電子相互作用にします.

すると例えば,
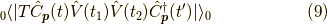
等の計算が必要になります.この場合,一つの相互作用の  には二つずつ生成演算子と消滅演算子
が入っているので,式
には二つずつ生成演算子と消滅演算子
が入っているので,式 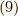 には五個ずつの生成演算子と消滅演算子が入っていることになります.
には五個ずつの生成演算子と消滅演算子が入っていることになります.
ここで振り返りをしておきます.自由な電子グリーン関数は,
でした.( 電子とフォノンのグリーン関数 の式 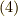 )
)
一方,時間並進で系が不変と考えるのは自然な事だと思いますが,
それを考えると,同時刻の
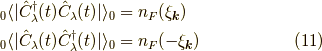
となります.( 電子とフォノンのグリーン関数 の式 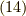 )
)
つまり,生成消滅演算子のペアは同時刻か異時刻で値の種類が変わるのです.
また重要な注意として,  の基底状態
の基底状態 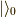 で挟まれる演算子は
生成と消滅がそれぞれ同数でないと期待値がゼロになってしまいます.
これは粒子数の異なる波動関数が直交する為です.
で挟まれる演算子は
生成と消滅がそれぞれ同数でないと期待値がゼロになってしまいます.
これは粒子数の異なる波動関数が直交する為です.
ウィックの定理
さあ,予告通り相互作用のあるグリーン関数を自由なグリーン関数で展開しましょう. それをウィックの定理と言います.証明は飛ばします.
【ルール1】
まず,量子数 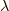 が異なる演算子のペアの期待値はゼロになります.
つまり,
が異なる演算子のペアの期待値はゼロになります.
つまり, 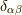 が必ず付いて
が必ず付いて

となります.生成消滅演算子の非ゼロ値を出す組み合わせはトータルで偶数個ですから,次は四つの展開です.
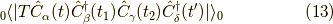
これは 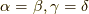 または
または 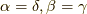 以外の時はゼロになります.
更に,もう一歩踏み込んで四次の期待値はそれぞれに時間順序積が付いた二次の期待値の多項式に分解できます.
その際,添え字
以外の時はゼロになります.
更に,もう一歩踏み込んで四次の期待値はそれぞれに時間順序積が付いた二次の期待値の多項式に分解できます.
その際,添え字 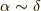 の交換はフェルミオン演算子の交換の際の符号変化の約束を守ります.
つまり,
の交換はフェルミオン演算子の交換の際の符号変化の約束を守ります.
つまり,

このペアの数はまず  個の消滅演算子を固定しましょう.そして,
個の消滅演算子を固定しましょう.そして, 個の生成演算子を全ての並び替えで対応させます.つまり,
個の生成演算子を全ての並び替えで対応させます.つまり, 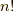 個の項が出てくるわけです.
個の項が出てくるわけです.
【ルール2】
電子とフォノン等の異種の演算子が混在しているとき,同種の交換はその粒子の性質に応じ,異種は常に符号変化なく交換する.そして異種の演算子が対になることは無いです.

【ルール3】
フォノン演算子もペアリングできます.交換で符号は変わりません.
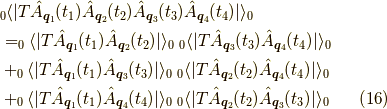
この組み合わせの数は  個の演算子があるとして,
個の演算子があるとして,
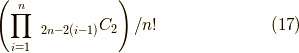
個の項が出てくると思います.  で
で  ,
, 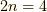 で
で  これは合っていそうです.
これは合っていそうです.
そして,物理的に可能なのは 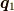 のフォノンを作って
のフォノンを作って 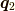 のフォノンを消すと言う事は,フォノンには生成と消滅の区別が無いため
のフォノンを消すと言う事は,フォノンには生成と消滅の区別が無いため  でなければなりません.結局は,
でなければなりません.結局は,
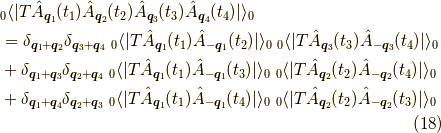
となります.
【ルール4】
同時刻の演算子の期待値は粒子数演算子になります.
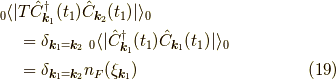
ボゾンの場合は,
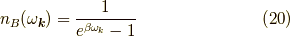
【ルール5】
異なる時刻の演算子の期待値はグリーン関数になります. 慣習として,生成演算子が右側に来るようにします. その際,符号変化はお忘れず.
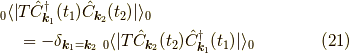
具体例を出しておきましょう.先ほどの例で言えば,
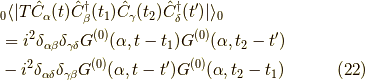
であり,
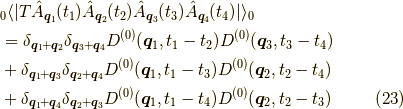
となります.この様にウィックの定理は時間順序された高次の期待値が全ての可能な時間順序されたペアリングによって表せると言う事を言っています.このウィックの定理が有効なのは 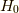 に含まれる生成消滅演算子が一個ずつの時だけです.それにはご注意を.
に含まれる生成消滅演算子が一個ずつの時だけです.それにはご注意を.
ウィックの定理の実践例(電子フォノン相互作用)
電子-フォノン相互作用の場合にこれを用いて近似値を出してみましょう.
ただし,グリーン関数の分母にある位相因子の 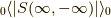 は無視します.
式
は無視します.
式  を使います.再掲すると,
を使います.再掲すると,
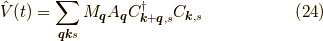
これを使います.すると,2次までの近似で
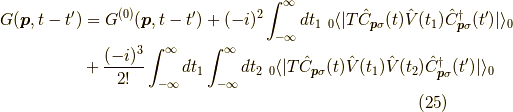
ここで,右辺第二項のフォノンの1次は期待値がゼロになるので
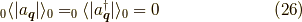
同様の理由で奇数次のボゾンの期待値はゼロです. 計算を進めると,
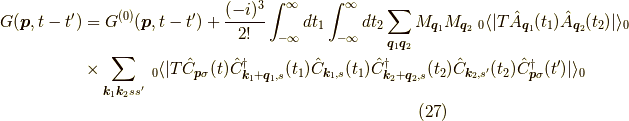
二次近似項のフォノン部分は,
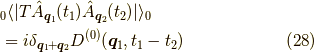
二次近似項の電子部分は,
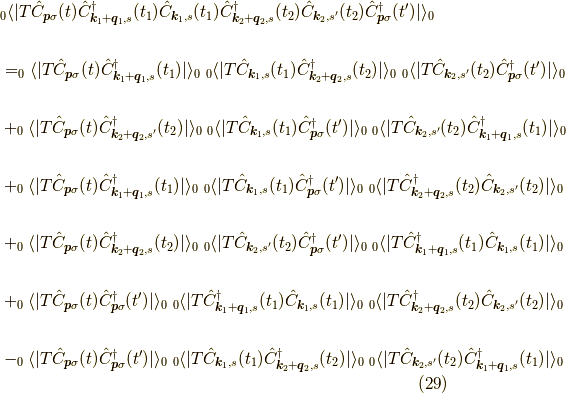
長いので一旦切ります.式はさらに変形でき,
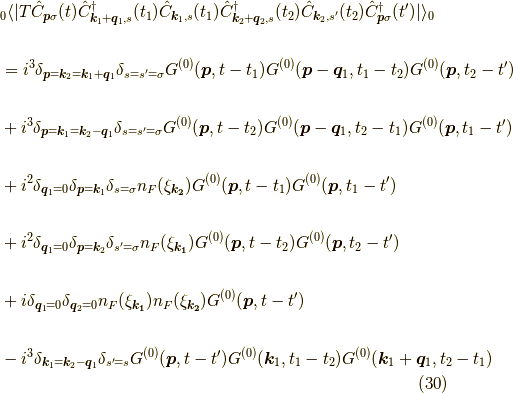
となります.この一連の変形は項の順番は入れ替えておらず,順に対応しています. 次回はこれをファインマンダイアグラムという図と対応させて理解します.
今日はここまで,お疲れ様でした.
次の記事は ファインマンダイアグラム です.