グリーン関数を理解しよう(相関関数の計算)
これからいくつかの記事を通して,
物性物理で扱われる絶対零度におけるグリーン関数の理解を目指します.
いくつかの定理などの証明は省略して,要点の俯瞰をする方針で行きます.
参考文献として,下に書くMahan先生の本を挙げて
おきます.このシリーズでは 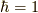 とします.
前の記事は 相互作用表示とS行列 です.
次の記事は 電子とフォノン です.( 目次 )
とします.
前の記事は 相互作用表示とS行列 です.
次の記事は 電子とフォノン です.( 目次 )
グリーン関数の意味
(典型的なフェルミオンである)電子のグリーン関数を挙げましょう.
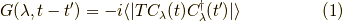
ここで,  は粒子を特徴づける量子数(主に運動量とスピン
は粒子を特徴づける量子数(主に運動量とスピン 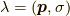 ),
), 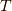 は時間順序演算子です.係数の
は時間順序演算子です.係数の  は全体の位相の固定(一つこれを選ぶと,他も全てこの因子に合わせて相対的に考えなければならない)であり,フーリエ変換後の関数形が綺麗になるように選んでいるのだと思います.また基底状態ベクトル
は全体の位相の固定(一つこれを選ぶと,他も全てこの因子に合わせて相対的に考えなければならない)であり,フーリエ変換後の関数形が綺麗になるように選んでいるのだと思います.また基底状態ベクトル 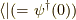 と
と 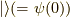 は,相互作用のある時の(
は,相互作用のある時の( 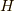 の)基底状態を表しています.
の)基底状態を表しています.
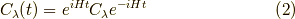
はハイゼンベルク表示での粒子の消滅演算子です.そして 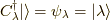 は相互作用のない時の(
は相互作用のない時の(  )の固有状態で完全系をなします.
)の固有状態で完全系をなします.
式 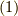 は階段関数
は階段関数

を用いて,
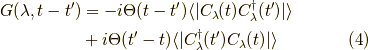
とも書けます.
第一項を考えましょう.この時  です.
です.
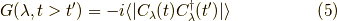
これは 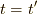 において基底状態に状態
において基底状態に状態  の電子一個を生成し(励起し),
その後の
の電子一個を生成し(励起し),
その後の 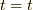 において,電子を消滅させることを意味しています.
において,電子を消滅させることを意味しています.
ゲルマン・ロウの相関関数
さて, 前回 のゲルマン・ロウの定理を思い出しましょう.再掲すると,
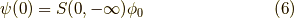
というものでした. また,位相因子
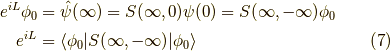
も使うので書いておきます.
これを 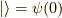 ,
,  として,この記事の記法で書くと,
として,この記事の記法で書くと,

となります.
そして, 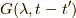 を書き直すにあたって,演算子は相互作用表示ではキャレット
を書き直すにあたって,演算子は相互作用表示ではキャレット  を付けて区別すると,
を付けて区別すると,
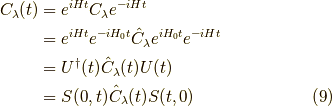
となります.すると,
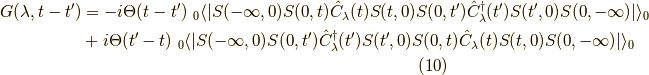
と書けます.さらに変形していきましょう.式 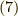 と
と 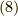 から,
から,
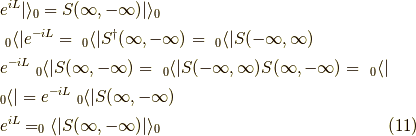
が言えるので,
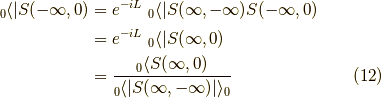
も言えます.すると,グリーン関数は,
![G(\lambda,t-t^\prime) &= \dfrac{-i}{_0 \langle | S(\infty,-\infty) | \rangle_0} [ \Theta(t-t^\prime) \ _0 \langle | S(\infty,t) \hat{C}_\lambda(t) S(t,t^\prime) \hat{C}^\dagger_\lambda(t^\prime) S(t^\prime,-\infty) | \rangle_0 \\&- \Theta(t^\prime-t) \ _0 \langle | S(\infty,t^\prime) \hat{C}^\dagger_\lambda(t^\prime) S(t^\prime,t) \hat{C}_\lambda(t) S(t,-\infty) | \rangle_0 ]\tag{13}](./e0cc02c9895c5bd4b8ac182a803b8426.png)
ここで時間順序積の強力さを思い知らされます. 第一項は,
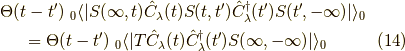
となります.実際には  には
には  を含むいろんな時間での切れ目があって,それが時間順序に整列させる作用を持つ
を含むいろんな時間での切れ目があって,それが時間順序に整列させる作用を持つ 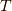 の下では,全てを
の下では,全てを 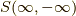 としてまとめてしまった表記でも良いと言う事です.計算の手間は変わらず,表記のみが簡単になった感じです.
としてまとめてしまった表記でも良いと言う事です.計算の手間は変わらず,表記のみが簡単になった感じです.
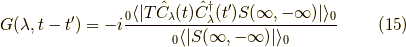
これを Wikipedia では相関関数と呼んでいます.
ここで 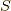 や
や 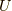 による時間発展は相互作用表示によるものであり,
による時間発展は相互作用表示によるものであり,  も同じ表示であることから,
表示が統一されていることにご注意ください.
も同じ表示であることから,
表示が統一されていることにご注意ください.
グリーン関数と確率
ここで最後に量子力学の復習をしましょう.状態 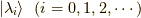 があったとします.
この時,
があったとします.
この時,  が完全系を張るなら,
が完全系を張るなら,  を使って,任意の状態
を使って,任意の状態 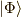 は
は
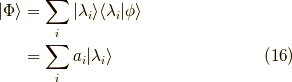
と展開されます.この 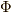 の中に
の中に 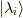 が入っている確率は,
が入っている確率は,

となるのでした.マタック(下参考文献)の議論をお借りしましょう.
式 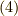 を見てみましょう.
を見てみましょう.  であり,
であり,
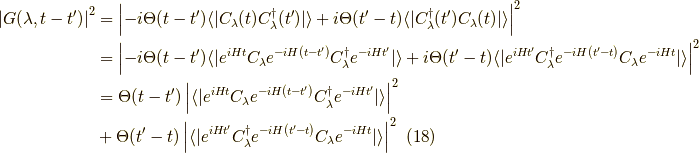
ここで,クロスタームの  はゼロとしました.
はゼロとしました.
(一応,積分時に 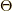 同士の積は測度0だと言えますが,この参考文献の
同士の積は測度0だと言えますが,この参考文献の 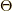 の定義,式
の定義,式  は,もしかしたら
は,もしかしたら
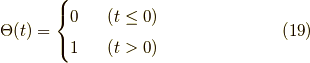
とした方が, 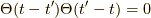 を言えるので,良いのかもしれません.)
を言えるので,良いのかもしれません.)
さて最終辺の第一項を考えましょう.この時,  であり
であり 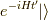 は
は  の相互作用有りの基底状態を
の相互作用有りの基底状態を 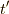 だけ進めた時間の状態です.そこで
だけ進めた時間の状態です.そこで 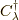 で状態
で状態  の電子を一つ作り出します.そして,系はさらに
の電子を一つ作り出します.そして,系はさらに 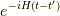 で
で 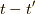 だけ時間発展をし,
だけ時間発展をし, 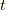 になります.それが,
になります.それが,

の意味です.一方, 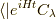 の解釈をしましょう.これはケットに直すと,
の解釈をしましょう.これはケットに直すと,

ですから,時刻 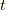 において粒子
において粒子  を加えた状態です.
を加えた状態です.
つまり,
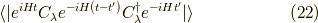
は 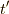 で加えられた基底状態中の粒子
で加えられた基底状態中の粒子  が時間発展を
が時間発展を 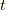 までした状態が,時刻
までした状態が,時刻 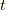 における基底状態に加えられた粒子
における基底状態に加えられた粒子  の状態の中に含まれる確率振幅となります.実際,この確率振幅の絶対値の二乗は
の状態の中に含まれる確率振幅となります.実際,この確率振幅の絶対値の二乗は 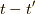 が経過した時に系が
が経過した時に系が  に居続ける確率です.
に居続ける確率です.
最終辺の第二項も同様に基底状態から粒子  を消す(ホールを作る)という並行な議論が出来ます.
を消す(ホールを作る)という並行な議論が出来ます. 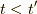 にはご注意を.
にはご注意を.
結局,これらは後に説明する( こちら )ホールを時間に逆行する向きの矢印を持つ電子と考えると,
どちらの過程も 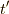 から
から 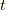 へ向かう矢印に関する確率振幅だと分かります.
へ向かう矢印に関する確率振幅だと分かります.
こういうグリーン関数の様な量は物理では非常に重要な量です.

もし本来 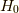 の固有状態である
の固有状態である  が
が 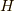 の固有状態でもあったとしましょう.
(また,
の固有状態でもあったとしましょう.
(また,  もまた
もまた 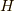 の基底状態であり,つまり,固有状態でもあります.)
この時,
の基底状態であり,つまり,固有状態でもあります.)
この時, 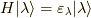 ,
, 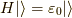 ですから,
ですから,
![G(\lambda, t>t^\prime) = -i \exp [-i(t-t^\prime)(\varepsilon_\lambda - \varepsilon_0)]\tag{23}](./3ce72930bc972486717eee5e3ea3fef1.png)
となり, 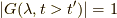 より,位相が変わるだけで状態は変化しないと分かります.
より,位相が変わるだけで状態は変化しないと分かります.
今日はここまで,お疲れ様でした.
次の記事は 電子とフォノン です.