三角関数の微分2
三角関数の微分1 でイメージをとらえたので,今度は解析的に公式を導いてみます.それには導関数の定義
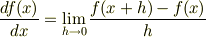
を使います.この定義から素直に考えるだけです.
sin関数の導関数
導関数の定義において, 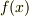 を
を 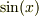 に置き換えると
に置き換えると
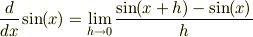
です.ここからどうしたらいいでしょうか. 三角関数に慣れている人なら,つぎの公式が思い浮かぶでしょう.
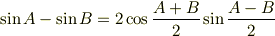
三角関数同士の足し算を積にする関係式です.微分積分の計算では, 三角関数の足し算を積に変えたり,その逆をしてみるとうまくいくことが多いです. というわけで積の形に変形してみます.
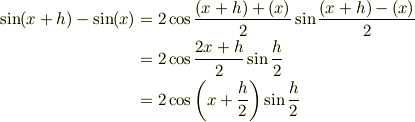
したがって,導関数の定義の式は
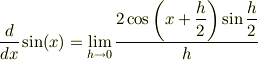
となり,分子が積の形になりました.分母分子を2で割ると
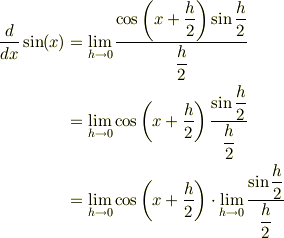
ここで 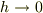 の極限にもって行けば導関数が得られます.
の極限にもって行けば導関数が得られます.
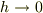 のとき
のとき 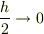 になるのはいいですよね.
分子がゼロになるのだから分数全体でもゼロです.ですから
になるのはいいですよね.
分子がゼロになるのだから分数全体でもゼロです.ですから
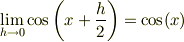
です. 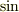 の方の極限ですが,
の方の極限ですが,
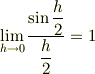
となるのは良いでしょうか. この証明ははさみうちの方法で行いますが,ここでは公式として使います.以上より
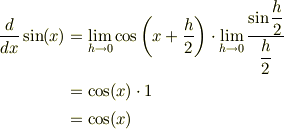
となり, 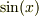 の導関数が
の導関数が 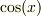 であることが導かれました.
であることが導かれました.
2階微分したらどうなる?
三角関数の導関数は重要な性質をもちます.それは,2階微分すると関数の形は変わらず, 符号だけ反転するという性質です.つまり,
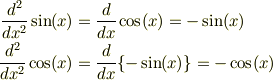
ということです.実数の範囲では,このような性質をもつ関数は三角関数だけです. この性質により,三角関数は単振動の方程式
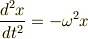
の解になっています.上式に 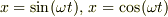 を
代入して計算すると両辺が等しくなるので,確かに解(特解)になっていることが確認できます.
を
代入して計算すると両辺が等しくなるので,確かに解(特解)になっていることが確認できます.
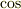 関数の導関数も同様の方法で導くことができます.
関数の導関数も同様の方法で導くことができます.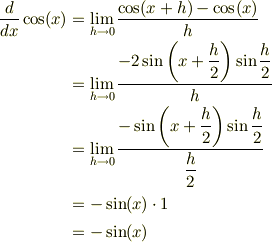
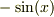 であることが導かれました.
であることが導かれました.