三角関数の微分1
三角関数を続けて微分して行くと, 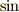 や
や 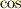 の繰り返しになりますよね.
たとえば,
の繰り返しになりますよね.
たとえば, 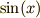 の微分は
の微分は
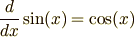
ですし, 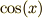 の微分は
の微分は
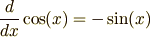
です.2階微分,3階微分となると,これがどんどん繰り返されていくわけです. 使っているうちに公式として覚えてしまいますが, そもそも三角関数の微分とは何を意味しているのでしょうか. ここでは,できるだけ視覚的なイメージから,三角関数の微分の意味をとらえて行きたいと思います.
sin(x) の接線の傾き
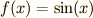 のグラフはつぎのようなものです.
のグラフはつぎのようなものです.
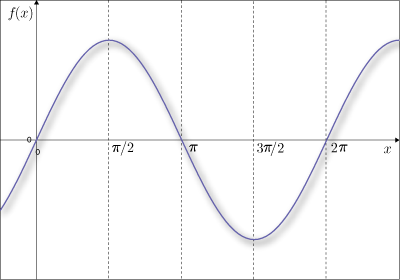
縦軸に 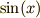 ,横軸に
,横軸に  をとっています.微分とはそもそも,接線の傾き(の関数)を求める操作です.
このグラフに,接線の傾きを書き込みますと
をとっています.微分とはそもそも,接線の傾き(の関数)を求める操作です.
このグラフに,接線の傾きを書き込みますと
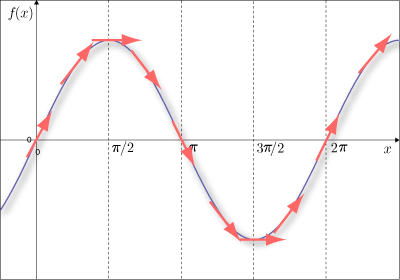
というふうになります.この接線の傾きに注目しましょう.
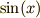 のグラフ自体が
のグラフ自体が  軸と交わる部分,すなわち
軸と交わる部分,すなわち 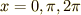 で,
接線の傾きが最大もしくは最小になることが分かります.
傾きが最大,というのは最も急に右上に傾いている部分,ということです.
で,
接線の傾きが最大もしくは最小になることが分かります.
傾きが最大,というのは最も急に右上に傾いている部分,ということです.
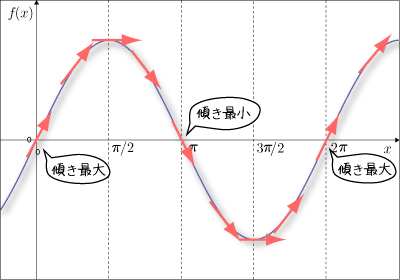
また,接線の傾きがゼロになるのは 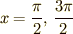 の点です.
の点です.
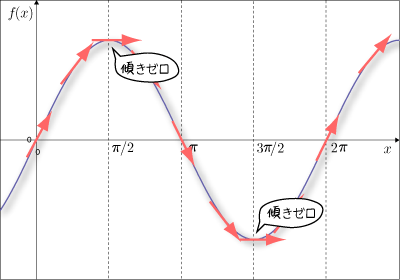
sin(x) の微分のグラフ
微分のグラフとは,この接線の傾きのグラフです.
縦軸のスケールは気にしないでおいて,接線の傾きの情報をグラフにてみます.
横軸は先ほどと同じ,縦軸には 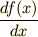 ,つまり接線の傾きをとります.
傾きの最大,最小,ゼロの情報から,つぎのように点を打てます.
,つまり接線の傾きをとります.
傾きの最大,最小,ゼロの情報から,つぎのように点を打てます.
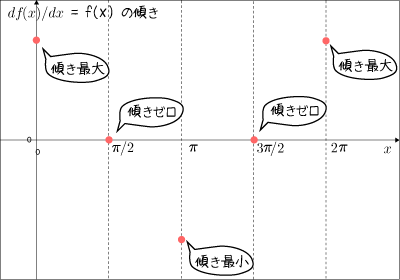
さらに,それぞれの点の間の中途半端な部分も点で埋めます.
最初に 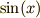 のグラフの接線の傾きを描いてみましたから,
なんとなくつぎのようになることが分かると思います.
のグラフの接線の傾きを描いてみましたから,
なんとなくつぎのようになることが分かると思います.
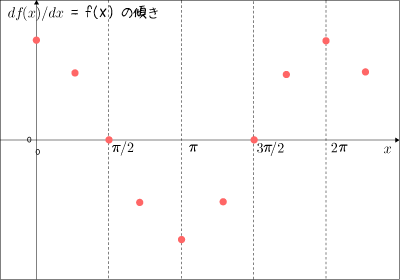
さらに点をたくさん打ちまして,滑らかにつなぐと
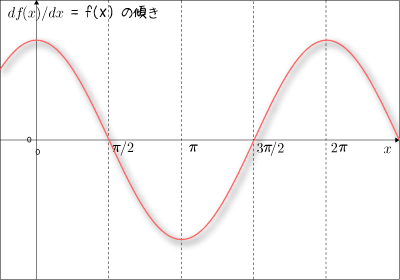
というものになります.これは見たことありますね. 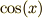 のグラフです.
これで,
のグラフです.
これで, 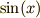 の微分が
の微分が 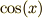 になるということが,
グラフの直感的イメージから導かれたことになります.
になるということが,
グラフの直感的イメージから導かれたことになります.
cos(x) の微分のグラフ
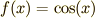 のグラフに対して,同様のことを行ってみます.
すると最終的にはつぎのグラフが得られます.
のグラフに対して,同様のことを行ってみます.
すると最終的にはつぎのグラフが得られます.
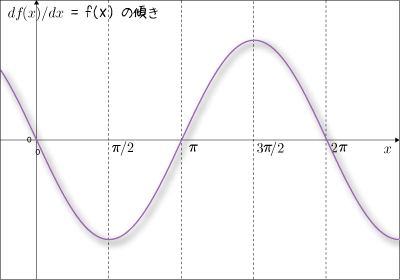
これは 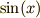 のグラフと比べて上下が正反対ですから,
のグラフと比べて上下が正反対ですから, 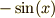 のグラフである,
と言うことができます.したがって,
のグラフである,
と言うことができます.したがって, 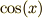 の微分は
の微分は 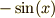 であるということも分かりました.
であるということも分かりました.
「微分とは接線の傾きである」というイメージさえつかんでいれば, このように三角関数の微分も,図形から直感的に理解することが可能です.