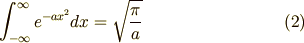ガウス積分の公式
物理を学んでいると,頻繁に出てくる積分というのがあります. その一つが ガウス積分 です.
ガウス積分
ガウス積分とは,つぎのような式で書かれる積分のことです.

ここで  は実数,
は実数,  は正の定数です.
は正の定数です.
ガウス積分の公式の証明
いくら公式だとはいっても,一度は本当にそうなることを確認しておきたいものです. この公式の証明は院試で頻出ですので,その道を目指す方は覚えておくと良いでしょう.
まず,左辺の積分値を 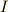 とします.
とします. 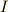 は被積分関数の関数形から,定義域が
は被積分関数の関数形から,定義域が 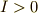 であることがわかります.
であることがわかります. 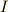 は,
は,
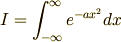
と書いても,
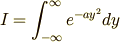
と書いても,積分値に変わりはありませんね.
したがって,
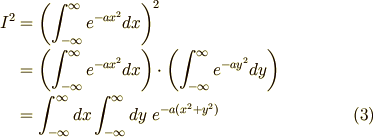
と変形していくことができます.
ここで 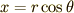 ,
, 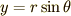 と変数変換をします.また,無限遠で積分領域を矩形から円形へと変形します.被積分関数が無限遠で速やかに0に収束することから,このようにしても積分値は変わりません.すると (3) 式は,
と変数変換をします.また,無限遠で積分領域を矩形から円形へと変形します.被積分関数が無限遠で速やかに0に収束することから,このようにしても積分値は変わりません.すると (3) 式は,
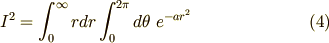
と書けます. 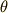 については積分を実行することができて,さらに式変形をしていくと
については積分を実行することができて,さらに式変形をしていくと
![I^2 & = 2 \pi \int_0^{\infty} r dr \ e^{-a r^2} \\ & = 2 \pi \int_0^{\infty} d\left( \frac{r^2}{2} \right) \ e^{-a r^2} \\ & = \pi \left[ -\frac{1}{a} e^{-a t} \right]_{t = 0}^{t = \infty} \\ & = \frac{\pi}{a} \tag{5}](./195871020bee3f64e6b01f4e774b4f50.png)
となります.ただし 2行目から 3行目で見やすいように,積分変数 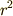 を
を 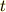 に置換しています.
に置換しています.
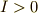 なので,正の値のみをとって
なので,正の値のみをとって
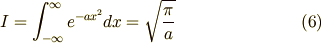
となり,ガウス積分の公式を得ることができました.